洛谷 P3956 棋盘 （BFS）

Posted 2020-10-14

题目链接：https://www.luogu.org/problemnew/show/P3956

题目：

题目描述

有一个m × m的棋盘，棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。

任何一个时刻，你所站在的位置必须是有颜色的（不能是无色的）， 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时，如果两个格子的颜色相同，那你不需要花费金币；如果不同，则你需要花费 1 个金币。

另外， 你可以花费 2 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用， 而且这个魔法的持续时间很短，也就是说，如果你使用了这个魔法，走到了这个暂时有颜色的格子上，你就不能继续使用魔法； 只有当你离开这个位置，走到一个本来就有颜色的格子上的时候，你才能继续使用这个魔法，而当你离开了这个位置（施展魔法使得变为有颜色的格子）时，这个格子恢复为无色。

现在你要从棋盘的最左上角，走到棋盘的最右下角，求花费的最少金币是多少？

输入输出格式

输入格式：

 

数据的第一行包含两个正整数 m， n，以一个空格分开，分别代表棋盘的大小，棋盘上有颜色的格子的数量。

接下来的 n 行，每行三个正整数 x， y， c， 分别表示坐标为（ x， y）的格子有颜色 c。

其中 c=1 代表黄色， c=0 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为（ 1, 1），右下角的坐标为（ m, m）。

棋盘上其余的格子都是无色。保证棋盘的左上角，也就是（ 1， 1） 一定是有颜色的。

 

输出格式：

 

输出一行，一个整数，表示花费的金币的最小值，如果无法到达，输出-1。

 

输入输出样例

输入样例#1： 复制

5 7
1 1 0
1 2 0
2 2 1
3 3 1
3 4 0
4 4 1
5 5 0

输出样例#1： 复制

8

输入样例#2： 复制

5 5
1 1 0
1 2 0
2 2 1
3 3 1
5 5 0

输出样例#2： 复制

-1

说明

输入输出样例 1 说明

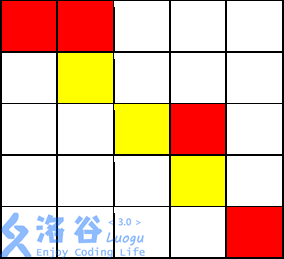
从（ 1， 1）开始，走到（ 1， 2）不花费金币

从（ 1， 2）向下走到（ 2， 2）花费 1 枚金币

从（ 2， 2）施展魔法，将（ 2， 3）变为黄色，花费 2 枚金币

从（ 2， 2）走到（ 2， 3）不花费金币

从（ 2， 3）走到（ 3， 3）不花费金币

从（ 3， 3）走到（ 3， 4）花费 1 枚金币

从（ 3， 4）走到（ 4， 4）花费 1 枚金币

从（ 4， 4）施展魔法，将（ 4， 5）变为黄色，花费 2 枚金币，

从（ 4， 4）走到（ 4， 5）不花费金币

从（ 4， 5）走到（ 5， 5）花费 1 枚金币

共花费 8 枚金币。

输入输出样例 2 说明

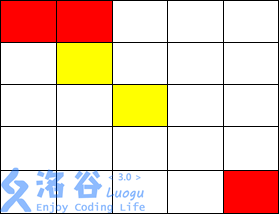
从（ 1， 1）走到（ 1， 2），不花费金币

从（ 1， 2）走到（ 2， 2），花费 1 金币

施展魔法将（ 2， 3）变为黄色，并从（ 2， 2）走到（ 2， 3）花费 2 金币

从（ 2， 3）走到（ 3， 3）不花费金币

从（ 3， 3）只能施展魔法到达（ 3， 2），（ 2， 3），（ 3， 4），（ 4， 3）

而从以上四点均无法到达（ 5， 5），故无法到达终点，输出－1

数据规模与约定

对于 30%的数据， 1 ≤ m ≤ 5， 1 ≤ n ≤ 10。

对于 60%的数据， 1 ≤ m ≤ 20， 1 ≤ n ≤ 200。

对于 100%的数据， 1 ≤ m ≤ 100， 1 ≤ n ≤ 1,000。

题意：求个最少花费

题解：用个数组记录下最小花费，然后一直搜到无法再更新成更小的花费的时候。注意一下两个格子都是没颜色的时候处理。（下一题就AC不了了，原来我是普及组的水平，捂脸（....）

 1 #include <queue>
 2 #include <cstring>
 3 #include <iostream>
 4 #include <algorithm>
 5 using namespace std;
 6 
 7 const int INF=0x3f3f3f3f;
 8 int M,N,X,Y,C,tmp;
 9 int Map[111][111];
10 int min_cost[111][111];
11 int dx[4]={0,0,-1,1};
12 int dy[4]={-1,1,0,0};
13 struct node{
14     int x,y,c,cost,change;
15 };
16 
17 void bfs(){
18     queue <node> Q;
19     node t1,t2;
20     t1.x=1;t1.y=1;t1.c=Map[1][1];t1.cost=0,t1.change=0;
21     Q.push(t1);
22     while(!Q.empty()){
23         t1=Q.front();Q.pop();
24         for(int i=0;i<4;i++){
25             t2.x=t1.x+dx[i];t2.y=t1.y+dy[i];t2.c=Map[t2.x][t2.y];
26             if(t2.x<1||t2.y<1||t2.x>M||t2.y>M) continue;
27             if(t2.c!=-1){
28                 if(t1.c==t2.c) tmp=t1.cost;
29                 else tmp=t1.cost+1;
30                 if(tmp<min_cost[t2.x][t2.y]) {t2.change=0;min_cost[t2.x][t2.y]=t2.cost=tmp;Q.push(t2);}
31             }
32             else{
33                 if(t1.change!=1){
34                     tmp=t1.cost+2;
35                     if(tmp<min_cost[t2.x][t2.y]){
36                         min_cost[t2.x][t2.y]=t2.cost=tmp;t2.change=1;t2.c=t1.c;
37                         Q.push(t2);
38                     }
39                 }
40             }
41 
42         }
43     }
44     if(min_cost[M][M]==INF) cout<<-1<<endl;
45     else cout<<min_cost[M][M]<<endl;
46 }
47 
48 int main(){
49     memset(Map,-1,sizeof(Map));
50     memset(min_cost,0x3f,sizeof(min_cost));
51     cin>>M>>N;
52     for(int i=1;i<=N;i++){
53         cin>>X>>Y>>C;
54         Map[X][Y]=C;
55     }
56     bfs();
57     return 0;
58 }