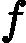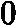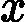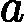梯度提升树(GBDT)原理小结
Posted change_world
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了梯度提升树(GBDT)原理小结相关的知识，希望对你有一定的参考价值。
在集成学习之Adaboost算法原理小结中，我们对Boosting家族的Adaboost算法做了总结，本文就对Boosting家族中另一个重要的算法梯度提升树(Gradient Boosting Decison Tree, 以下简称GBDT)做一个总结。GBDT有很多简称，有GBT（Gradient Boosting Tree）, GTB（Gradient Tree Boosting ）， GBRT（Gradient Boosting Regression Tree）, MART(Multiple Additive Regression Tree)，其实都是指的同一种算法，本文统一简称GBDT。GBDT在BAT大厂中也有广泛的应用，假如要选择3个最重要的机器学习算法的话，个人认为GBDT应该占一席之地。
1. GBDT概述
GBDT也是集成学习Boosting家族的成员，但是却和传统的Adaboost有很大的不同。回顾下Adaboost，我们是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。GBDT也是迭代，使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同。
在GBDT的迭代中，假设我们前一轮迭代得到的强学习器是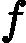
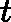
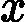
ft−1(x), 损失函数是
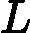
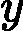
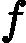
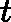
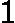
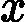
L(y,ft−1(x)), 我们本轮迭代的目标是找到一个CART回归树模型的弱学习器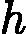
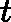
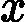
ht(x)，让本轮的损失损失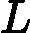
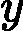
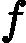
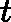
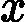
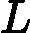
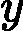
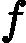
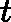
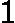
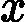
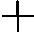
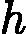
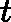
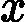
L(y,ft(x)=L(y,ft−1(x)+ht(x))最小。也就是说，本轮迭代找到决策树，要让样本的损失尽量变得更小。
GBDT的思想可以用一个通俗的例子解释，假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。
从上面的例子看这个思想还是蛮简单的，但是有个问题是这个损失的拟合不好度量，损失函数各种各样，怎么找到一种通用的拟合方法呢？
2. GBDT的负梯度拟合
在上一节中，我们介绍了GBDT的基本思路，但是没有解决损失函数拟合方法的问题。针对这个问题，大牛Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树。第t轮的第i个样本的损失函数的负梯度表示为
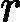
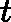
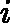
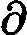
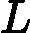
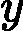
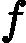
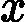
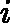
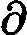
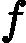
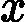
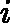
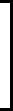
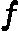
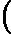
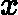
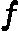
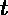
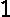
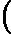
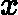
rti=−[∂L(y,f(xi)))∂f(xi)]f(x)=ft−1(x)
利用
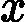
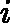
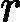
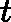
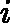
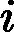
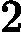
(xi,rti)(i=1,2,..m),我们可以拟合一颗CART回归树，得到了第t颗回归树，其对应的叶节点区域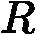
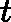
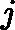
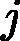
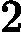
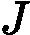Rtj,j=1,2,...,J。其中J为叶子节点的个数。
针对每一个叶子节点里的样本，我们求出使损失函数最小，也就是拟合叶子节点最好的的输出值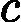
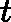
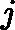ctj如下：
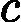
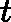
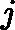
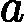
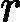
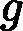
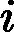
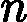
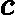
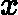
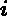
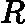
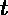
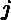
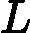
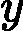
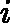
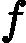
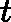
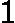
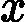
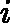
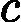
ctj=argmin⏟c∑xi∈RtjL(yi,ft−1(xi)+c)
这样我们就得到了本轮的决策树拟合函数如下：
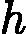
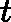
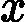
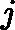
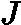
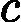
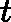
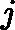
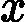
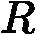
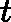
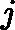
ht(x)=∑j=1JctjI(x∈Rtj)
从而本轮最终得到的强学习器的表达式如下：
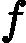
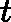
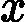
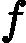
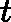
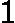
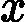
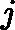
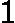
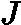
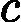
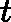
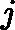
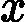
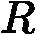
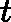
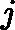
ft(x)=ft−1(x)+∑j=1JctjI(x∈Rtj)
通过损失函数的负梯度来拟合，我们找到了一种通用的拟合损失误差的办法，这样无轮是分类问题还是回归问题，我们通过其损失函数的负梯度的拟合，就可以用GBDT来解决我们的分类回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。
3. GBDT回归算法
好了，有了上面的思路，下面我们总结下GBDT的回归算法。为什么没有加上分类算法一起？那是因为分类算法的输出是不连续的类别值，需要一些处理才能使用负梯度，我们在下一节讲。
输入是训练集样本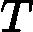
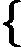
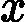
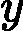
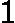
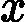
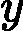
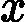
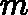
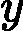
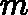
T={(x,y1),(x2,y2),...(xm,ym)}， 最大迭代次数T, 损失函数L。
输出是强学习器f(x)
1) 初始化弱学习器
