差分约束
Posted 大米饼
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了差分约束相关的知识,希望对你有一定的参考价值。
这里有一大堆不等式或者等式形成的限制条件,题目通常会问问你是否存在合法方案或者让你求出合法方案。——————————差分约束
·前言:
一个概括的定义是,一些不等式组可以视作一个差分约束系统。简单而言,就是给出许多不等式,然后我们需要给每个未知数填上值,使它们满足所有给出的关于它们的不等式——这正是这类问题的求解过程。由于这一过程类似于最短路算法中的松弛操作,因此解决差分约束问题成了最短路算法的一个美妙而重要用途!
·一个例题
这里呢有一个长度为n的序列,现在给出m条信息,每条信息是一个三元组{l,r,w}表示这个序列的区间[l,r]之内的元素之和为w。现在需要我们判断是否存在满足条件的序列(Yes or No)。
先想想怎么样的信息可以使得没有满足条件的序列?很容易,只需要产生一个矛盾就可以了: ( {1,3,10} {4,5,20} {1,5,29} )。
既然给出的信息都是区间和,那么我们可以使用前缀S[i]来做以下事情:
这里为了满足上述三个约束条件,我们可以写出这三个式子:
S[i]表示[1,i]的元素和,S[0]=0
①S[0]+10=S[3] ②S[3]+20=S[5] ③S[0]+29=S[5]
至此,只是按照题目输入的信息得到了几个迷迷糊糊的等式,怎么快速判断一般情况的矛盾依旧很吃力。
·从不等式到最短路
为什么说是"不等式"而不是"等式"?仅仅是为了统一化——任何等式可以表示为两个不等式(a+b=c --> a+b<=c&&a+b>=c),因此让我们从更加一般化的不等式开始入手吧。
这样一来,我们需要寻求一种方式,高效判断不等式组 ai+wi<=bi (这里统一了不等式的格式)。一个笨笨的想法是,我们先去保证部分不等式满足条件,再去使得其他不等式满足,最终使得所有的不等式满足。这显得很笼统而天真,举一个例子来说明这个笨笨地想法具体怎样操作:
考虑错综复杂的不等关系:假如此时b1已经有一个值了,但是a1发现b1比自己加上w1的值要小……怎么办?因此a1决定将b1修改到刚刚好的位置,即此时赋值: b1=a1+w1。刚刚好?是的。据此,我们发现,只要一个ai发现某个bi的值不符合它的要求,它就会把这个bi强制修改为刚刚满足条件的值。这一步操作我们写成代码就长这样:
这个图片足以让我们将其与最短路算法的松弛操作相联系。从这个图来看,如果要转化为最短路,那么必须要建一张图(额其实这里是最长路,不过呢这两者本质没区别)。根据图中信息可以发现,a到b建了一条权值为w[i]的边。
·所以此问题我们的建图策略是:
对于不等式:ai + wi <= bi,将点ai向bi建一条边权为wi的边。
·我们试图去满足所有不等式的过程是:
进行最长路算法。之所以进行最长路,从建边和不等式的符号上就可以看出来了。注意最长路还是最短路与求解问题需要的最值是最小值还是最大值并无联系。最长最短仅仅由不等式决定:
例如,将上述式子变形: bi - wi >= ai,那么我们在写if语句的时候,里面的内容就是if(b[i]+(-w[i])<a[i]),因此我们发现如果建图方式改为从b向a建边边权为-wi的话,我们的算法从最长路变成了最短路。
·怎么才叫出现了矛盾(即不存在解):
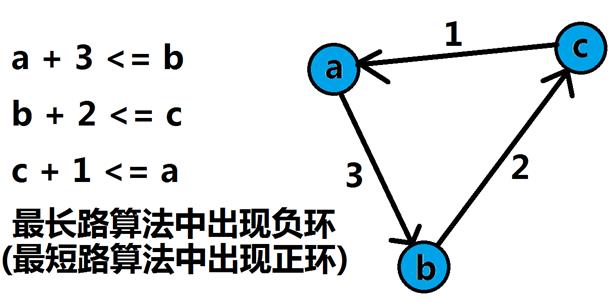
我们知道,对于每个a,如果那个b的值不满足条件,a就会去更新b的值,此过程在最长路中体现为松弛操作。那么如果存在一个矛盾不等式组,那么就会不断解决矛盾,如图:
上述三个不等式明显矛盾。据此我们发现所建图中的正环(或者最短路的负环)正是某几个不等式矛盾的直接体现。
·最长路(最短路)的距离初始化问题。对于最长路,首先所有点的dis值都赋值为inf,然后起点的值赋值为0。为什么起点赋值为0呢?这是因为我们先假设起点值是0,然后通过最短路算法来约束,依然会找到一个合法解或者负环。但是,很多情况下,最短路将谁做为起点,起点值赋值为多少还是视题目而定。
一个值得注意的点是,我们发现我们写下的不等式符号与最短路松弛操作的if()中符号是相反的,意义是:不满足则修改。
至于为什么上文a修改b要修改到刚刚好的问题,这和题目要求最值有关,在接下来的例题中将会获得深刻而美妙的感受。
[1]狡猾的商人_
·述大意:
就是上文的那个例题。一个长度为n的序列,现在给出m条信息(n<100,m<1000),每条信息是一个三元组{l,r,w}表示这个序列的区间[l,r]之内的元素之和为w。现在需要我们判断是否存在满足条件的序列(Yes or No)。
·分析:
(一)建立不等式组
设S[i]表示序列1~i的元素之和(前缀和)。
对于每个约束条件(l,r,w),则有:[l-1]+w=S[r]
转化为不等式为:S[l-1]+w<=S[r]且S[r]-w<=S[l-1]
(注意这里统一了不等式的格式)
(二)建图
进行最长路算法。对于每个不等式ai + wi <= bi,
建边ai--->bi,边权为wi。那么上述每个三元组建边为:
①ADD(l-1,r,w) ②ADD(r,l-1)
(三)矛盾判定
由于数据很小,此处使用Floyd进行最长路,初始化为dis[i][i]=0。如果算法进行完后出现了某一个点i满足dis[i][i]!=0,说明出现了正环,输出NO。
·代码:
注意代码中用的是最短路
1 #include<stdio.h> 2 #include<algorithm> 3 #define inf 1000000007 4 #define go(i,a,b) for(int i=a;i<=b;i++) 5 int T,n,m,l,r,v,d[102][102],bad; 6 int main() 7 { 8 scanf("%d",&T); 9 while(T--&&scanf("%d%d",&n,&m)) 10 { 11 go(i,0,n)go(j,0,n)d[i][j]=i==j?0:inf;bad=0; 12 go(i,1,m)scanf("%d%d%d",&l,&r,&v),d[l-1][r]=v,d[r][l-1]=-v; 13 go(k,0,n)go(i,0,n)go(j,0,n)d[i][j]=std::min(d[i][j],d[i][k]+d[k][j]); 14 go(i,0,n)if(d[i][i]!=0)bad=1,i=n;puts(bad?"false":"true"); 15 } 16 return 0; 17 }//Paul_Guderian
[2]区间们_
·述大意:
有一个长度为50000的序列,输入一个n表示给出了n个约束。要求我们标记序列上的一些元素。每个约束为{a,b,c}表示区间[a,b]中至少有c个元素被标记。如果可以满足所有约束,输出标记元素的最小个数。保证有解。
·分析:
(一)建立不等式组
设S[i]表示序列1~i的被标记的元素个数(前缀和)。
那么对于每个约束(a,b,c)满足:S[a-1] + c <= S[b]
另外,由于每个位置只有选与不选之分,所以这里还有一个限制:
1>=S[i]-S[i-1]>=0
上述约束条件统一格式为:
①S[a-1]+c<=S[b] ②S[i] + 0<=S[i+1] ③S[i] -1<=S[i-1]
(二)建图
进行最长路算法。上述三个约束条件建图如下:
①ADD(ai-1,bi,ci) ②ADD(i,i+1,0) ③ADD(i,i-1,-1)
图的起点为约束中最小的左端点,终点为约束中最大的右端点。
(三)矛盾判断?啊,这道题保证了没有矛盾呀。
·代码:
SPFA求最长路
1 #include<queue> 2 #include<stdio.h> 3 #include<algorithm> 4 #define inf 1000000007 5 #define go(i,a,b) for(int i=a;i<=b;i++) 6 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v) 7 const int N=50010; 8 using namespace std; 9 bool inq[N];queue<int>q; 10 struct E{int v,next,w;}e[N<<1]; 11 int n,a[N],b[N],c[N],head[N],k=1,S=1e9,T,d[N]; 12 void ADD(int u,int v,int w){e[k]=(E){v,head[u],w};head[u]=k++;} 13 14 void Build() 15 { 16 go(i,1,n)scanf("%d %d %d",a+i,b+i,c+i); 17 go(i,1,n)S=min(S,a[i]-1),T=max(T,b[i]); 18 go(i,1,n)ADD(a[i]-1,b[i],c[i]); 19 go(i,S+1,T)ADD(i,i-1,-1); 20 go(i,S,T-1)ADD(i,i+1,0); 21 } 22 23 void SPFA() 24 { 25 go(i,S,T)d[i]=-inf;d[S]=0;q.push(S);int u; 26 while(!q.empty()){inq[u=q.front()]=0;q.pop();fo(i,head,u) 27 if(d[u]+e[i].w>d[v])d[v]=d[u]+e[i].w,!inq[v]?q.push(v),inq[v]=1:1;} 28 } 29 30 int main() 31 { 32 scanf("%d",&n);Build(); 33 SPFA();printf("%d\\n",d[T]); 34 return 0; 35 }//Paul_Guderian
[3]广告_
·述大意:
有一个长度为20000的序列,输入一个n,k(1<=k,n<=1000)表示给出了n个约束。要求我们标记序列上的一些元素。每个约束为{a,b}表示区间[a,b]中至少有min(k,区间长度)个元素被标记。如果可以满足所有约束,输出一种标记方案。保证有解。
·分析:
(一)建立不等式组
同上题,只不过每个不等式ai+wi<=bi中的wi被统一为min(k,b-a+1)。
(二)建图
进行最长路算法。上述三个约束条件建图如下:
①ADD(ai-1,bi,ci) ②ADD(i,i+1,0) ③ADD(i,i-1,-1)
图的起点为约束中最小的左端点,终点为约束中最大的右端点。
(三)输出一种方案
这不难,最后只需要看看,如果dis[i]>dis[i-1],说明i被标记了。
·代码:
SPFA求最长路。
1 #include<queue> 2 #define _ 10010 3 #include<stdio.h> 4 #include<algorithm> 5 #define inf 1000000007 6 #define go(i,a,b) for(int i=a;i<=b;i++) 7 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v) 8 using namespace std; 9 const int N=30003; 10 queue<int>q;bool inq[N]; 11 struct E{int v,next,w;}e[N<<1]; 12 int n,K,k=1,a[N],b[N],head[N],S=1e9,T,d[N]; 13 void ADD(int u,int v,int w){e[k]=(E){v,head[u],w};head[u]=k++;} 14 15 void Build() 16 { 17 go(i,1,n)scanf("%d%d",a+i,b+i),a[i]+=_,b[i]+=_; 18 go(i,1,n)if(a[i]>b[i])a[i]^=b[i]^=a[i]^=b[i]; 19 go(i,1,n)ADD(a[i]-1,b[i],min(b[i]-a[i]+1,K)); 20 go(i,1,n)S=min(S,a[i]-1),T=max(T,b[i]); 21 go(i,S,T)ADD(i,i-1,-1); 22 go(i,S,T)ADD(i,i+1,0); 23 } 24 25 void SPFA() 26 { 27 go(i,S,T)d[i]=-inf;d[S]=0;q.push(S);int u; 28 while(!q.empty()) 29 { 30 inq[u=q.front()]=0;q.pop(); 31 fo(i,head,u)if(d[u]+e[i].w>d[v]) 32 { 33 d[v]=d[u]+e[i].w; 34 !inq[v]?q.push(v),inq[v]=1:1; 35 } 36 } 37 printf("%d\\n",d[T]); 38 go(i,S,T)if(d[i]>d[i-1])printf("%d\\n",i-_); 39 } 40 41 int main() 42 { 43 scanf("%d%d",&K,&n); 44 45 Build(); SPFA(); 46 47 return 0; 48 }//Paul_Guderian
[4]放置奶牛_
·述大意:
给出一个长度为n的牛序列,输入n,m1,m2表示有两类约束条件,前m1个约束条件(a,b,d)表示在a位置的牛与在b位置的牛相距不大于d。接下来m2个约束条件(a,b,d)表示在a位置的牛与在b位置的牛相距不小于d。另外,下标小的牛不能下标大的牛后面。输入保证a<b。如果能够求出1与n的最远距离,则输出。如果1,n的最远距离无限制,则输出-2。若有矛盾,则输出-1。(n<=1000,m1,m2<=10000)
·分析:
(一)建立不等式组
设x[i]表示i号牛所在的位置。对于每个约束(a,b,d):
1类约束:a+d>=b 2类约束:b-d>=a
(二)建图
对于每个约束条件,建图为:
1类约束:ADD(a,b,d) 2类约束:ADD(b,a,-d)
(三)问题判定
使用最短路算法。初始化d[1]=0,那么最终d[n]的值就是1到n的距离了。如果算法完成后,d[n]=inf,说明没有限制,输出-2。如果出现负环,则输出-1。否则输出d[n]表示距离。
·代码:
由于不一定有负环,因此BFS_SPFA依旧更加优秀。(有个读入优化qaq)
1 #include<queue> 2 #include<stdio.h> 3 #define inf 1000000007 4 #define go(i,a,b) for(int i=a;i<=b;i++) 5 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v) 6 const int N=2003;bool inq[N]; 7 struct E{int v,next,w;}e[N*200]; 8 int n,X,Y,A,B,D,head[N],k=1,d[N],negative; 9 void ADD(int u,int v,int w){e[k]=(E){v,head[u],w};head[u]=k++;} 10 11 inline char Getchar() 12 { 13 static char C[1000000],*p1,*p2; 14 if(p1==p2)p2=(p1=C)+fread(C,1,1000000,stdin); 15 if(p1==p2)return EOF;return *p1++; 16 } 17 18 inline void Read(int &x) 19 { 20 x=0;char c=Getchar(); 21 while(c<\'0\'||c>\'9\')c=Getchar(); 22 while(c>=\'0\'&&c<=\'9\')x=x*10+c-\'0\',c=Getchar(); 23 } 24 25 void Build() 26 { 27 go(i,1,X)Read(A),Read(B),Read(D),ADD(A,B,D); 28 go(i,1,Y)Read(A),Read(B),Read(D),ADD(B,A,-D); 29 go(i,2,n)ADD(i,i-1,0); 30 } 31 32 std::queue<int>q; 33 void SPFA() 34 { 35 go(i,1,n)d[i]=inf;d[1]=0;q.push(1);int vis[N]={0}; 36 while(!q.empty()){int u=q.front();q.pop();inq[u]=0; 37 fo(i,head,u)if(d[u]+e[i].w<d[v]) 38 { 39 d[v]=d[u]+e[i].w; 40 if(++vis[v]>n){negative=1;return;} 41 !inq[v]?q.push(v),inq[v]=1:1;} 42 } 43 } 44 45 int main() 46 { 47 Read(n);Read(X);Read(Y); 48 49 Build(); SPFA(); 50 51 if(negative){puts("-1");return 0;} 52 if(d[n]==inf){puts("-2");return 0;} 53 if(d[n]!=inf){printf("%d\\n",d[n]);return 0;} 54 }//Paul_Guderian
[5]矩阵_
·题目:
有一个n*m的矩阵,初始每个格子的权值都为0,可以对矩阵执行两种操作:
1. 选择一行,该行每个格子的权值加1或减1。
2. 选择一列,该列每个格子的权值加1或减1。
现在有K个限制,每个限制为一个三元组(x,y,c),代表格子(x,y)权值等于c。问是否存在一个操作序列,使得操作完后的矩阵满足所有的限制。如果存在输出”Yes”,否则输出”No”。
·分析:
(一)建立不等式组
我们发现每次只能对于整行整列操作,并且每个点最终的值就是所在的行列的所加所减的值的和。因此,将每行每列看成一个点分别用i和(i+n)表示。对于每行i,val[i]表示+1操作和-1操作次数的差值。对于每一列j,val[j]表示-1操作和+1操作的差值,那么对于每个限制(x,y,z),则有:
val[x] + z = val[y]
转化为不等式:val[x]+z>=val[y+n], val[y]-z>=val[x]
(二)建图
对于上述约束条件,建边为:
①ADD(x,y,z) ②ADD(y,x,-z)
(三)矛盾判断:
建立超级源点连向所有点并进行最短路算法。如果出现负环则不存在满足条件的操作组合。
·代码:
SPFA判负环。
1 #include<queue> 2 #include<stdio.h> 3 #define inf 1000000007 4 #define go(i,a,b) for(int i=a;i<=b;i++) 5 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v) 6 const int N=2010; 7 struct E{int v,next,w;}e[N<<2]; 8 int T,n,m,K,head[N],k,x,y,v,S,d[N],vis[N];bool inq[N],bad; 9 void ADD(int u,int v,int w){e[k]=(E){v,head[u],w};head[u]=k++;} 10 11 bool SPFA() 12 { 13 std::queue<int>q;d[S]=0; 14 while(!q.empty())q.pop();q.push(S);int u; 15 while(!q.empty()) 16 { 17 inq[u=q.front()]=0;q.pop(); 18 fo(i,head,u)if(d[u]+e[i].w<d[v]) 19 { 20 d[v]=d[u]+e[i].w; 21 if((++vis[v])>(n+m))return 0; 22 if(!inq[v])inq[v]=1,q.push(v); 23 } 24 } 25 return 1; 26 } 27 28 int main() 29 { 30 scanf("%d",&T); 31 while(T--&&scanf("%d%d%d",&n,&m,&K)) 32 { 33 go(i,0,n+m)d[i]=inf,head[i]=inq[i]=vis[i]=0;bad=0;k=1; 34 go(i,1,K)scanf("%d%d%d",&x,&y,&v),ADD(x,y+n,v),ADD(y+n,x,-v); 35 go(i,1,n+m)ADD(S,i,0);puts(SPFA()?"Yes":"No"); 36 } 37 return 0; 38 }//Paul_Guderian
[6]节日_
·题目:
有n个正整数X1,X2,...,Xn,再给出m1+m2个限制条件,限制分为两类:
1. 给出a,b (1<=a,b<=n),要求满足Xa + 1 = Xb
2. 给出c,d (1<=c,d<=n),要求满足Xc <= Xd
在满足所有限制的条件下,求集合{Xi}大小的最大值。无解输出NIE。
·分析:
(一)建立不等式组
首先这题意需要理解清楚。意思是将n个数赋值后,去重后的个数的最大值。还是按照题目给的建立不等式吧。但是这里设x[i]表示i号的值,想一想初值怎么处理(等一会儿讲啊)?建立不等式如下:
①x[a]+1=x[b] ==> x[a]+1<=x[b],x[a]+1>=x[b]
②x[c]<=x[d]
(二)建图
根据不等式,建图如下:
①ADD(a,b,1),ADD(b,a,-1)
②ADD(c,d,0)
(三)啊?
本题我们用最长路算法。我们发现建出来的图很是混乱。原因是我们的目标是求出最大的元素种类数,然而直接SPFA是有错误的: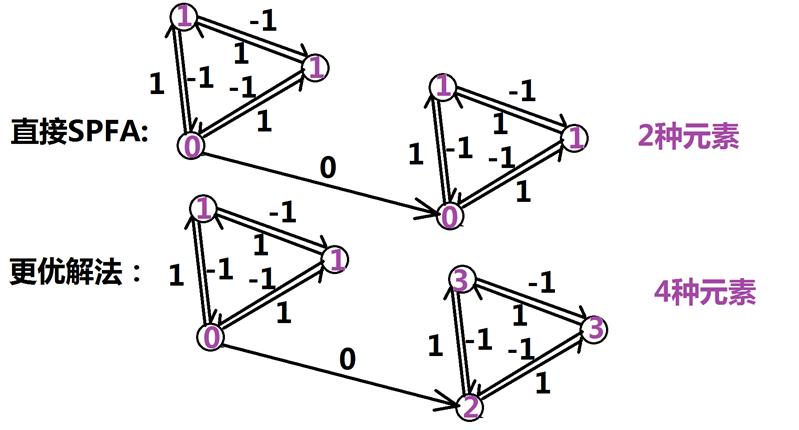
我们发现图中出现了强联通分量,并且桥一定是边权为0的那种边(①类边已经成环,不可能是桥)。然后我们最初的SPFA错在走过桥的时候直接将两点的值赋值成相同的了,但实际上完全可以把另一端赋值为一个与前面都不相同的值(如图)。
我们得出了结论,不在同一连通分量的点实际上取值是不会有相互限制的,因此我们的最短路算法仅适用于一个强联通分量内,假如我们求出了每个强联通分量的最优值,那么加起来就是最终的答案。
如何求出每个连通分量的最大种类数?由于差分约束的SPFA在这里是合法的,因此我们只需要找出这里面的最长路就是答案了(恩这个画图可以很好地理解),简单解释原因就是在合法的前提下,每一条路径代表了一种合法的。最后一点就是初始化,将每个点弄成0,然后在连通分量内进行Floyd就可以了。如果出现了正环,直接跳出输出-1就是了。
·代码:
Tarjan缩点+Floyd啦啦。
1 #include<stdio.h> 2 #include<algorithm> 3 #define inf 1000000007 4 #define go(i,a,b) for(int i=a;i<=b;i++) 5 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v) 6 const int N=620; 7 using namespace以上是关于差分约束的主要内容,如果未能解决你的问题,请参考以下文章