机器学习算法-python实现svm支持向量机—理论知识介绍

Posted 2020-07-03 lcchuguo

(转载请注明出处：http://blog.csdn.net/buptgshengod)

1.背景

     强烈推荐阅读（http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982639.html）  

       支持向量机SVM（support vector machines）。

SVM是一种二值分类器，是近些年比較流行的一种分类算法。

本文，首先要介绍一些主要的知识概念，在下一章将对SVM进行简单地代码实现。

2.基本概念

（1）线性可分

          

       首先介绍一下什么叫线性可分，引用一张上一节的图。

线性可分实际上就是能够用一条直线将两种不同的点区分开来。

由此我们能够得到线性不可分就是两种点混合在一起不能区分。

可是线性不可分的点事实上也能够用数学方法区分开来。

比方说一个四维的数据集我们能够用一个三维的对象将其分开，这个对象叫做超平面。

下图的超平面就是那条蓝线。

（2）支持向量

       支持向量，如今我们知道了超平面的概念。支持向量事实上就是距离超平面在近期的向量。

以上图为例，就是距离蓝线近期的那些点。方法就是点到线的距离判定。

一旦我们找到了这些支持向量，那么我们就能够放大这些向量，仅仅考虑这些对象，用到的是序列最小优化的思想。

（3）拉格朗日乘子法

       对于支持向量的求法，我们须要一定的约束条件。

比方说我们设点到超平面的距离是d，我们要求取d>1的点作为约束条件。

由于假设没有这个约束条件会使得计算出现误差。

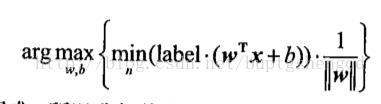这个公式是我们去点到超平面距离最小的点的集合，且满足

。

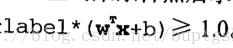在存在约束条件情况下求极值的问题。我们用到拉格朗日乘子法（參见百度百科）。

（4）变型

   參照拉格朗日公式F(x1,x2,...λ)=f(x1,x2,...)-λg(x1,x2...)。我们把上面的式子变型为

 约束条件就变成了

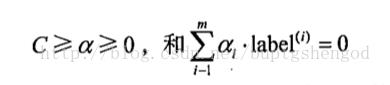
上式的參数c使松弛变量，由于我们看到图中一些红点被分到了绿点的范围里，为了考虑到这样的问题，引入一个变量来控制。

svm的主要任务是计算參数C。