2017 ACM区域赛现场赛 青岛站 E （polya计数）

Posted 2020-10-13

题目链接（暂无）

吐槽：这场比赛感觉对我感觉还算友好，虽然Q群知乎上命题方已经被喷死了，C语言上机题还有字符串题有大腿队友轻松搞定，网络流恰是我能想出来的，E本来也应该是在能力范围内，不过因为之前没写过跑程序搜置换的题，一时看到就发怵。。万幸过掉了K题网络流拿到了金，不然场上没写E打铜得后悔死我。。

题意：一个3*3*1的长方体，有3*3（顶面）+3*4（侧面）+3*3（底面）=30个待染色的小面，长方体有四个可扭动的轴，位于四条边的中间那个1*1*1的小块，每次可扭动180°。支持的基本的置换为上下翻转，绕中心旋转，将3*1*1的边绕轴扭动。给定颜色数c和模数p，求总的非等价染色方案数模p的结果。

 

爆搜求置换；对每种置换求循环指数，从而得到循环指数为k（1<=k<=30）的循环个数；套用Polya公式

 

（注意p可能非质数所以会有一个特殊处理，见下图（tot为置换总数））

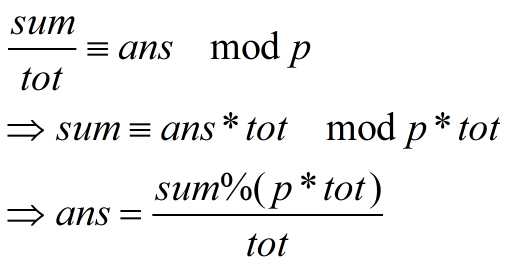
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef __int128 LLL;

const int N=30;
int ori[N]= {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29};

int tr[3][N]=
{
//    { 0, 1, 2, 3, 4, 5, 6, 7, 8,     9,10,11,12,13,14,15,16,17,18,19,20,        21,22,23,24,25,26,27,28,29},
    {29,25,24,23,22,21,28,27,26,    16,15,14,13,12,11,10,9 ,20,19,18,17,          5, 4, 3, 2, 1, 8, 7, 6, 0},
    {0,3,4,5,6,7,8,1,2,                12,13,14,15,16,17,18,19,20,9 ,10,11,        23,24,25,26,27,28,21,22,29},
    {0,23,22,21,4,5,6,7,8,            13,12,11,10,9 ,14,15,16,17,18,19,20,        3 ,2 ,1 ,24,25,26,27,28,29}
};

int ans[1600][N];
int tot;

void dfs(int cur)
{
    for(int i=0; i<3; i++)
    {
        int temp[N];
        for(int j=0; j<N; j++)
            temp[j]=ans[cur][tr[i][j]];
        int flag=1;
        for(int k=0; k<tot; k++)
        {
            int flag1=1;
            for(int j=0; j<N; j++)
                if(ans[k][j]!=temp[j]) flag1=0;
            if(flag1)    //flag1=true 表示 temp和某个ans[k]全等
            {
                flag=0;
                break;
            }
        }
        if(flag)    //flag=true 表示 temp和任意ans[k]不全等
        {
            for(int j=0; j<N; j++)
                ans[tot][j]=temp[j];
            tot++;
            dfs(tot-1);
        }
    }
}

int cnt[N];
int vis[N];
void dfs2(int x,int y[])
{
    vis[x]=1;
    if(!vis[y[x]]) dfs2(y[x],y);
}
void add(int y[])
{
    memset(vis,0,sizeof(vis));
    int t=0;
    for(int i=0;i<N;i++) if(!vis[i])
    {
        t++;
        dfs2(i,y);
    }
    cnt[t]++;
}

LLL qpow(LLL x,LLL n,LLL mod)
{
    LLL ret=1;
    for(;n;n>>=1)
    {
        if(n&1) ret=ret*x%mod;
        x=x*x%mod;
    }
    return ret;
}
LLL qpow(LLL x,LLL n)
{
    LLL ret=1;
    for(;n;n>>=1)
    {
        if(n&1) ret=ret*x;
        x=x*x;
    }
    return ret;
}
int main()
{
    for(int i=0; i<N; i++) ans[0][i]=ori[i];
    tot++;
    dfs(0);
    printf("%d\\n",tot);
    printf("\\n========================================\\n\\n");
    for(int i=0;i<tot;i++)
        add(ans[i]);
    for(int i=1;i<=N;i++)
        printf("%2d : %d\\n",i,cnt[i]);
    printf("\\n========================================\\n\\n");
    
    LL c,p;
    while(cin>>c>>p)
    {
        LLL sum=0;
        LLL b=tot*p;
//        for(int i=1;i<=N;i++)
//            sum+=cnt[i]*qpow(c,i);
//        sum/=tot;
//        cout<<(LL)(sum%p)<<endl;
        for(int i=1;i<=N;i++)
            sum=(sum+cnt[i]*qpow(c,i,b))%b;
        sum/=tot;
        cout<<(LL)sum<<endl;
    }
}