[LeetCode]*124.Binary Tree Maximum Path Sum
Posted phlsheji
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[LeetCode]*124.Binary Tree Maximum Path Sum相关的知识,希望对你有一定的参考价值。
【题目】
Given a binary tree, find the maximum path sum.
The path may start and end at any node in the tree.
For example:
Given the below binary tree,
1
/ 2 3
Return 6.
【分析】
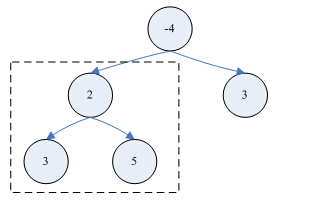
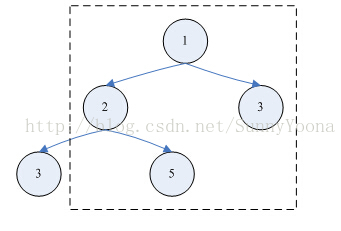
须要考虑以上两种情况:
1 左子树或者右子树中存有最大路径和 不能和根节点形成一个路径
2 左子树 右子树 和根节点形成最大路径
【代码】
/********************************* * 日期:2014-12-23 * 作者:SJF0115 * 题号: Binary Tree Maximum Path Sum * 来源:https://oj.leetcode.com/problems/binary-tree-maximum-path-sum/ * 结果:AC * 来源:LeetCode * 总结: **********************************/ #include <iostream> #include <climits> #include <algorithm> using namespace std; struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {} }; class Solution { public: int maxPathSum(TreeNode *root) { if(root == NULL){ return 0; }//if maxSum = INT_MIN; maxPath(root); return maxSum; } private: int maxSum; int maxPath(TreeNode *node){ if(node == NULL){ return 0; }//if // 左子树最大路径值(路径特点:左右节点仅仅能选一个) int leftMax = maxPath(node->left); // 右子树最大路径值(路径特点:左右节点仅仅能选一个) int rightMax = maxPath(node->right); // 以node节点的双側路径((node节点以及左右子树)) int curMax = node->val; if(leftMax > 0){ curMax += leftMax; }//if if(rightMax > 0){ curMax += rightMax; }//if maxSum = max(curMax,maxSum); // 以node节点的单側路径(node节点以及左右子树的一个) if(max(leftMax,rightMax) > 0){ return max(leftMax,rightMax) + node->val; } else{ return node->val; } } }; //按先序序列创建二叉树 int CreateBTree(TreeNode*& T){ int data; //按先序次序输入二叉树中结点的值,-1表示空树 cin>>data; if(data == -1){ T = NULL; } else{ T = (TreeNode*)malloc(sizeof(TreeNode)); //生成根结点 T->val = data; //构造左子树 CreateBTree(T->left); //构造右子树 CreateBTree(T->right); } return 0; } int main() { Solution solution; TreeNode* root(0); CreateBTree(root); cout<<solution.maxPathSum(root); }
【温故】
/*---------------------------------------
* 日期:2015-04-30
* 作者:SJF0115
* 题目: 124.Binary Tree Maximum Path Sum
* 网址:https://leetcode.com/problems/binary-tree-maximum-path-sum/
* 结果:AC
* 来源:LeetCode
* 博客:
-----------------------------------------*/
#include <iostream>
#include <vector>
using namespace std;
struct TreeNode{
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x):val(x),left(nullptr),right(nullptr){}
};
class Solution {
public:
int maxPathSum(TreeNode *root) {
if(root == NULL){
return 0;
}//if
int maxSum = INT_MIN;
maxPath(root,maxSum);
return maxSum;
}
private:
int maxPath(TreeNode *root,int &maxSum){
if(root == NULL){
return 0;
}//if
// 后序遍历
// root左子树最大路径值
int leftMax = maxPath(root->left,maxSum);
// root右子树最大路径值
int rightMax = maxPath(root->right,maxSum);
// 双側最大路径值
int curMax = root->val;
if(leftMax > 0){
curMax += leftMax;
}//if
if(rightMax > 0){
curMax += rightMax;
}//if
maxSum = max(maxSum,curMax);
// 假设是某节点的子树时仅仅能返回单側最大路径值
int oneSideMax = max(leftMax,rightMax);
if(oneSideMax > 0){
return root->val + oneSideMax;
}//if
else{
return root->val;
}
}
};
//按先序序列创建二叉树
int CreateBTree(TreeNode*& T){
int data;
//按先序次序输入二叉树中结点的值,-1表示空树
cin>>data;
if(data == -1){
T = NULL;
}
else{
T = new TreeNode(data);
//构造左子树
CreateBTree(T->left);
//构造右子树
CreateBTree(T->right);
}
return 0;
}
int main() {
Solution solution;
TreeNode* root(0);
CreateBTree(root);
cout<<solution.maxPathSum(root);
}
以上是关于[LeetCode]*124.Binary Tree Maximum Path Sum的主要内容,如果未能解决你的问题,请参考以下文章