洛谷 P3368 模板树状数组 2 如题（区间修改+单点查询）

Posted 2020-10-13 lpl_bys

P3368 【模板】树状数组 2

• 时空限制1s / 128MB

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数数加上x

2.求出某一个数的和

输入输出格式

输入格式：

 

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含2或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x 含义：输出第x个数的值

 

输出格式：

 

输出包含若干行整数，即为所有操作2的结果。

 

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

输出样例#1：

6
10

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

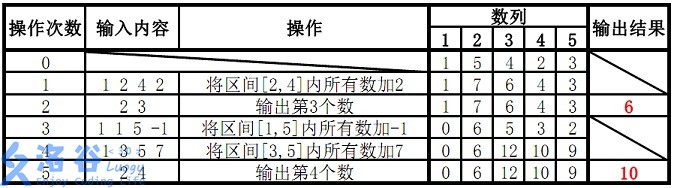
故输出结果为6、10

----------------------------------------------------------------------------------------------

推一篇博客：http://blog.csdn.net/qq_21841245/article/details/43956633

最主要的做法其实是差分数组

用树状数组维护数组的前缀和只是为了达到优化时间复杂度的目的

存板子：

 

 1 #include<stdio.h>
 2 #include<string.h>
 3 #define maxn 500010
 4 int delta[maxn],a[maxn],n,m;
 5 int read();
 6 int lowbit(int);
 7 void add(int,int);
 8 int find(int);
 9 int main(){
10     n=read(),m=read();
11     for(int i=1;i<=n;i++) a[i]=read();
12     for(int i=1;i<=m;i++){
13         int o=read();
14         if(o==1){
15             int x=read(),y=read(),k=read();
16             add(x,k);add(y+1,-k);
17         }
18         else{
19             int x=read();
20             int ans=find(x)+a[x];
21             printf("%d\n",ans);
22         }
23     }
24     return 0;
25 }
26 int find(int x){
27     int SUM=0;
28     while(x>0){
29         SUM+=delta[x];
30         x-=lowbit(x);
31     }
32     return SUM;
33 }
34 void add(int x,int k){
35     while(x<=n){
36         delta[x]+=k;
37         x+=lowbit(x);
38     }
39 }
40 int lowbit(int x){
41     return x&-x;
42 }
43 int read(){
44     int ans=0,f=1;char c=getchar();
45     while(‘0‘>c||c>‘9‘){if(c==‘-‘)f=-1;c=getchar();}
46     while(‘0‘<=c&&c<=‘9‘)ans=ans*10+c-48,c=getchar();return ans*f;
47 }

区间修改+单点查询