二叉树及存储结构

Posted 2020-10-13

本文的结构：

1. 二叉树的基本形态
2. 二叉树的重要性质
3. 二叉树的抽象数据类型定义
4. 二叉树的存储结构

---

 

二叉树T：一个有穷的节点集合。这个集合可以为空，若不为空，则它是由根节点和称为其左子树T_L和右子树T_R的两个不相交的二叉树组成

二叉树的五种基本形态：

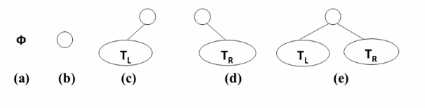
• (a) 空树
• (b) 有一个结点
• (c) 右子树为空
• (d) 左子树为空
• (e) 有左右子树

二叉树的重要性质：

• 一个二叉树第i层的最大节点数为：2^i-1，i >=1;
• 深度为k的二叉树有最大结点总数为 2^k-1,k>=1；
• 对任何非空二叉树T，若n₀表示叶节点的个数，n₂是度为2的非叶节点的个数，那么两者满足关系n₀=n₂+1；（如下图）
• 

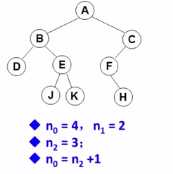
例题：有一颗二叉树，其两个儿子的结点个数为15个，一个儿子的结点个数为32个，问该二叉树的叶结点个数是多少？解：n₂=15，n₁=32，n₀=n₂+1=16;

二叉树的抽象数据类型定义

类型名称：二叉树

数据对象集：一个有穷的结点集合，若不为空，则由根节点和左右二叉子树组成

操作集：

1. Boolean IsEmpty（BinTree BT）：判断BT是否为空；
2. void Traversal（BinTree BT）：遍历，按某顺序访问每个结点
3. BinTree CreatBinTree()：创建一个二叉树

常见的遍历方法：

1. void PreOrderTraversal(BinTree BT)：先序---->根、左子树、右子树
2. void InOrderTraversal（BinTree BT）：中序--->左子树、根、右子树
3. void PostOrderTraversal(BinTree BT)：后序--->左子树、右子树、根
4. void LevelOrderTraversal(BinTree BT)：层次遍历--->从上到下、从左到右

二叉树的存储结构

• 顺序存储结构：（用数组实现），完全二叉树：从从上到下、从左到右顺序呢存储n个结点的完全二叉树的节点父子关系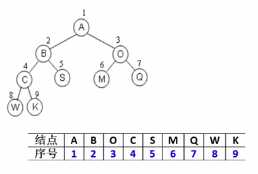；把结点放到数组里很简单，但是如何快速的找出结点之间的关系？一般二叉树也可以采用这这种结构（将二叉树补全），但会造成空间浪费。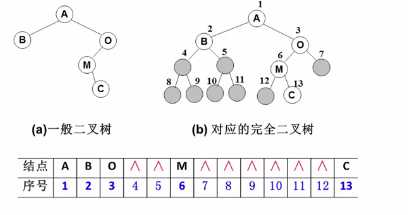
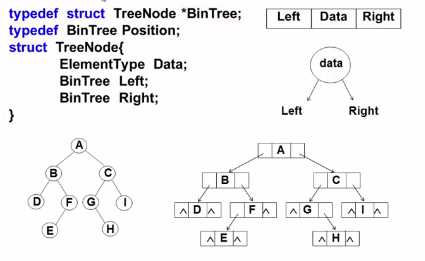
• 链表存储