#1038 : 01背包

Posted 2020-07-02 LzyRapX

#1038 : 01背包

时间限制:20000ms

单点时限:1000ms

内存限制:256MB

描述

且说上一周的故事里，小Hi和小Ho费劲心思终于拿到了茫茫多的奖券！而现在，终于到了小Ho领取奖励的时刻了！

小Ho现在手上有M张奖券，而奖品区有N件奖品，分别标号为1到N，其中第i件奖品需要need(i)张奖券进行兑换，同时也只能兑换一次，为了使得辛苦得到的奖券不白白浪费，小Ho给每件奖品都评了分，其中第i件奖品的评分值为value(i),表示他对这件奖品的喜好值。现在他想知道，凭借他手上的这些奖券，可以换到哪些奖品，使得这些奖品的喜好值之和能够最大。

提示一：合理抽象问题、定义状态是动态规划最关键的一步

提示一：合理抽象问题、定义状态是动态规划最关键的一步

小Hi想了想，问道：“你打算怎么做？”

“枚举2^N种可能的选取方案，先计算他们需要的奖券之和sum，在sum不超过M的情况下，计算他们的喜好值之和value，并统计一个最优的方案，也就是value的最大值！”天真的小Ho给出了一个同样天真的方案。

“简直白教你动态规划了……”小Hi不禁扶额道：“这道题目你还是考虑一下如何使用动态规划来解决吧！”

“好的！让我回忆一下……动态规划要求问题存在两种性质：重复子问题和无后效性~但是...我怎么也看不出这道题目怎么套上这两种性质呀，什么样算是一个子问题？”小Ho想了想，说道。

“先别急，你想要知道子问题是什么？那么首先，我们要想办法把我们现在遇到的问题给抽象化！”

小Ho低头思索了一会，说道：“唔，我想想，如果用best(x)表示手中有x张奖券时能够获取的最高的喜好值的和，那么我们的问题就是best(M)是多少？”

“你这样定义的话，是没有办法把‘求解best(M)’这样一个问题分解成不同的子问题的哦~”小Hi笑道：“也罢，初学者往往都很难自己想出如何好的抽象问题，这次就让我先来告诉你~”

“就知道卖关子~快说！”

小Hi笑了笑，继续说道：“这个问题——best(M)的求解，其实问的便是每个奖品是否选择是么？那么你在遍历这2^N种可能的选取方案的时候，是不是按照顺序，一一确定每一个奖品是否选取？”

“是的！”

小Hi继续道：“那么我们不妨就按照你遍历时的情况来，不过做一点小改动，以best(i, x)表示已经决定了前i件物品是否选取，当前已经选取的物品的所需奖券数总和不超过x时，能够获取的最高的喜好值的和。”

“听起来的确和搜索很像，搜索时就是按照编号从小到大的顺序一一决定每件物品是否选取，并且维护一个当前已经选取的物品的所需奖券书的总和。”忽然小Ho似乎想到了什么：“诶，那么这个best(i, x)其实就是和之前遇到的数字三角形迷宫问题中用于解决问题的记忆化搜索很相似的？”

“没错，记忆化搜索的确就是和动态规划极为相似，或者可以说，他们用以解决问题的原理是一样的。”小Hi回答道。

“原来如此，我想想……那么最终的答案其实就是best(N, M)是么？”小Ho得出了结论。

“是的！这个时候我们就可以称best(N, M)的求解为我们的问题了！”小Hi高兴道。

“那么子问题呢？”

小Hi挥了挥手示意小Ho不要着急：“子问题通常会采取将问题分成若干部分来进行，有的时候是均分，也有的时候仅仅是在规模上减一。比如这里，我们不妨考虑best(N, M)这个问题的最后一个决策——第N件奖品是否进行选择：首先，如果选择第N件奖品，当然首先要保证第N件商品所需的奖券数不超过M，我们可以知道这种方案的最佳收益为best(N - 1, M - need(N)) + value(N)。”

“其次呢，如果不选择第N件奖品，我们可以知道这种方案的最佳收益为best(N - 1, M)。”小Hi顿了顿，继续道：”由于第N件奖品只有选取和不选取两种可能，我们于是可以知道best(N, M) = max{best(N - 1, M - need(N)) + value(N), best(N - 1, M)}！”

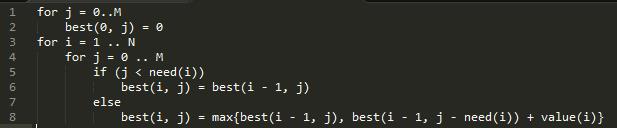
“没错！”小Ho道：“同样的道理，对于任意i>1, j，我们都可以知道best(i, j)=max{best(i-1, j-need(i)) + value(i), best(i - 1, j)}!”

“归纳的不错！那么你接检验一下这个问题的定义方法是否拥有动态规划所需要的两种性质？”

小Ho想了想，决定一条一条的来：“首先看重复子问题——这是动态规划之所以比搜索高效的原因，如果最后四件奖品分别为所需奖券为1，喜好值为1、所需奖券为2，喜好值为2、所需奖券为3，喜好值为3、所需奖券为4，喜好值为4的四个奖品，那么无论是选择1、4还是2、3，都会要求解best(N-4, M-5)这样一个子问题，而这个子问题只需要求解一次就能够进行计算，所以重复子问题这一性质是满足的。”

“没错，接着说。”

“其次再看无后效性……同样的，如果分别有所需奖券为1，喜好值为1、所需奖券为2，喜好值为2、所需奖券为3，喜好值为3、所需奖券为4，喜好值为4的四个奖品，那么无论是选取第1个和第4个，还是选取第2个和第3个，他们的所需奖券数都为5，喜好值之和都为5。所以我只需要知道best(4, 5)=5就够了，它为什么等于5对我而言没有区别，不会对之后的决策产生影响。这就是无后效性，所以想来也是满足的。

“说的挺正确~那么接下来要考虑的是如何使用best(i, j)=max{best(i-1, j-need(i)) + value(i), best(i - 1, j)}来求解每一个best(i, j)了~”小Hi道：“这部分我便直接告诉你吧，我们定义一个问题A依赖于另一个问题B当且仅当求解A的过程中需要事先知道B的值，那么我们很容易的发现best(i, j)是依赖于best(i-1, j-need(i))和best(i-1, j)两个问题的，也就是说这两个问题要先于best(i, j)进行求解~”

“所以我们只要按照i从小到大的顺序，以这样的方式进行计算，就可以了！”小Ho插嘴道。

“你又抢我台词！

提示二：说过了减少时间消耗，我们再来看看如何减少空间消耗

提示二：说过了减少时间消耗，我们再来看看如何减少空间消耗

且说小Ho搞清楚了计算方法，正在埋头苦写代码，在一旁看他写代码的小Hi是在看不下去了，决定再指点指点小Ho：“小Ho啊！”

“怎么了？”小Ho眼睛盯着屏幕，望都没望小Hi一眼。

“你现在是不是需要开一个N * M大小的二维数组best，来记录求解出的best值呀？”

小Ho终于有了点反应，抬起头来说道：“是啊，怎么了？“

“我有办法不用开这么大空间哦~”小Hi笑嘻嘻道：”可我就是不告诉你！”

“诶，别这样，我请你吃雪糕！”小Ho一听就急了，连忙许下了报酬。

“开玩笑啦~”小Hi也是随便逗了逗乐子就没继续：“你想想，在i已经是10以上的时候，best(5, j)这样的值还有用么？”

“没有用了……你是说，我并不需要在内存中存下来所有的best(i, j)，没有用了的值都可以不进行保存……也就是说，实际上只要开一个2*M大小的数组就可以了，然后像这样的方式进行来回的计算，是不是就可以了？”

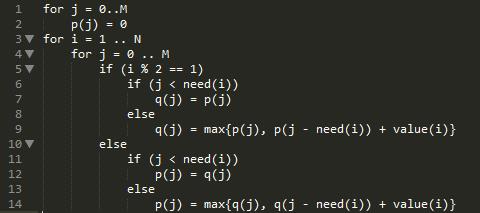
“是的呢！但是还可以更少哦~让我来写这个程序的话，我只需要开一个M大小的一维数组就可以了”小Hi自信的说道：“你想想，如果我按照j从M到1的顺序，也就是跟之前相反的顺序来进行计算的话。另外根据我们的状态转移方程，可以显然得出如果状态(iA, jA)依赖于状态(iB, jB)，那么肯定有iA = iB+1, jA>=jB。所以不难得出一个结论：我在计算best(i, j)的时候，因为best(i, j+1..M)这些状态已经被计算过了，所以意味着best(i - 1, k)，k=j..M这些值都没有用了——所有依赖于他们的值都已经计算完了。于是它们原有的存储空间都可以用来存储别的东西，所以我不仿直接就将best(i, j)的值存在best(i-1, j)原有的位置上，就像这样。”

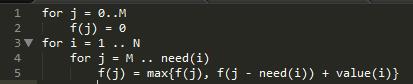
“原来还可以这样！这样一处理，不仅空间复杂度小了很多，代码也很好看了呢！”小Ho开心道。

“那你还不去写？”

输入

每个测试点（输入文件）有且仅有一组测试数据。

每组测试数据的第一行为两个正整数N和M,表示奖品的个数，以及小Ho手中的奖券数。

接下来的n行描述每一行描述一个奖品，其中第i行为两个整数need(i)和value(i)，意义如前文所述。

测试数据保证

对于100%的数据，N的值不超过500，M的值不超过10^5

对于100%的数据，need(i)不超过2*10^5, value(i)不超过10^3

输出

对于每组测试数据，输出一个整数Ans，表示小Ho可以获得的总喜好值。

样例输入

5 1000
144 990
487 436
210 673
567 58
1056 897

样例输出

2099

#include<cstdio>
using namespace std;
int main()
{
	int n,m;
	scanf("%d%d",&n,&m);
	int *need=new int[n];
	int* value=new int[n];
	for(int i=0;i<n;++i)
	   scanf("%d%d",need+i,value+i);
	int * f=new int[m]();
	for(int i=0;i<n;++i)
		for(int j=m;j>=need[i];--j)
			if(f[j]<f[j-need[i]]+value[i])
				f[j]=f[j-need[i]]+value[i];
	printf("%d\n",f[m-1]);
}

AC2:

#include<stdio.h>
#define max(a,b) a>b?a:b
#define N 505
#define M 100005
int best[N][M];
int need[N];
int value[N];


void dp(int n,int m)
{
	for(int i=1;i<=n;i++)
	{
		for(int j=0;j<=m;j++)
		{
			if(j>=need[i])
				best[i][j]=max(best[i-1][j],best[i-1][j-need[i]]+value[i]);
			else best[i][j]=best[i-1][j];
		}
	}
}
int main()
{
	int n,m;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&need[i],&value[i]);
	}
	for(int i=0;i<=m;i++)
	best[0][i]=0;
	
	dp(n,m);
	
	printf("%d\n",best[n][m]);
	
	
}