《算法导论》学习摘要chapter-6——堆排序

Posted 2020-07-02 絮雨清风

       本章堆排序内容是《算法导论》教材第二部分《排序与顺序统计量》的第一讲。

       堆排序，这是一种O（nlgn）时间的原址排序算法。它使用了一种被称为堆的数据结构，堆还可以用来实现优先级队列。

1、堆的概念

        数组R[1...n]中，n个关键字序列k1，k2，…，kn，当且仅当该序列满足如下性质（简称为堆性质，以大根堆为例）：

• ki >= k(2i）且ki >= k(2i+1)(1≤i≤ n/2）大根堆则换成>=号。相当于完全二叉树的非叶子结点，K(2i）则是左子节点，k(2i+1）是右子节点

         若将此序列所存储的向量R[1..n]看做是一棵完全二叉树的存储结构，则堆实质上是满足如下性质的完全二叉树：树中任一非叶子结点的关键字均不大于（或不小于）其左右孩子（若存在）结点的关键字。

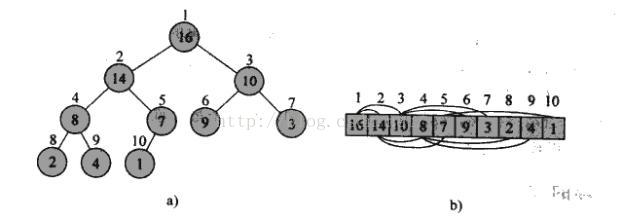
       二叉堆是一个数组，它可以被看成是一个近似的完全二叉树。树上的每一个结点对应数组中的一个元素。除了最底层外，该树是完全充满的，而且是从左到右填充。表示堆的数组A包括两个属性：A.length表示数组元素的个数；A.heap_size表示数组A有具有堆结构的元素个数。有：0=<A.heap_size=<A.length。A[1]是树的根节点。

        通常给定节点i，我们很容易得到可以根据其在数组中的位置求出该节点的父亲节点、左右孩子节点：

• PARENT(i) = i/2              //对位置i整除2即可得到当前结点的父结点
• LEFT(i)  = 2*i                 //对位置i乘2即可得到当期结点的左子结点
• RIGHT(i) = 2*i+1。      //对位置i乘2再加1，即可得到当期结点的右子结点

        在堆排序好的实现中，这三个函数通常以“宏”或者“内联函数”的方式来实现，比如：

#define PARENT(i)  i/2
#define LEFT(i)    i*2
#define RIGHT(i)   i*2+1

                                      

                                 

                                                   图1  a)二叉树，每个结点圆圈内部的数字是它所存储的数据           b)数组形式展现的一个最大堆。

          根据节点数值满足的条件，可以将分为最大堆和最小堆，最大堆和最小堆除了需要满足堆的性质外还要满足：

1. 最大堆的特性是：除了根节点以外的每个节点i，有A[PARENT(i)] >= A[i]；
2. 最小堆的特性是：除了根节点以外的每个节点i，有A[PARENT(i)] >=A[i]。

        在堆排序算法中，我们优先选择最大堆。最小堆通常用于构造优先队列。
　　把堆看成一个棵树，有如下的特性：

1. 含有n个元素的堆的高度是lgn；
2. 堆结构上的基本操作的运行时间与树高成正比，即时间复杂度为：O(nlgn)；
3. 当用数组表示存储了n个元素的堆时，最后一个非叶子节点是：n/2；叶子节点的下标是：n/2+1，n/2+2，……，n；
4. 在最大堆中，最大元素该子树的根上；在最小堆中，最小元素在该子树的根上。

2、维护堆的性质

        这里讲的维护堆的性质，主要是指维护堆当前节点的值都要大于左子节点值和右子节点值。当堆中数据变动时，通过维护函数能够调整树的结构中元素的位置，以使数组还能继续满足堆的性质。

       这里我们构造一个函数：max_heapify()用来维护最大堆性质的重要过程。在调用max_heapify()的时候，我们假定根节点为LEFT(i)和RIGHT(i)的二叉树都是最大堆。max_heapify()就是通过让A[i]的值在最大值中“下沉”，从而使得以下标i为根节点的子树重新满足最大堆的性质。

                                   

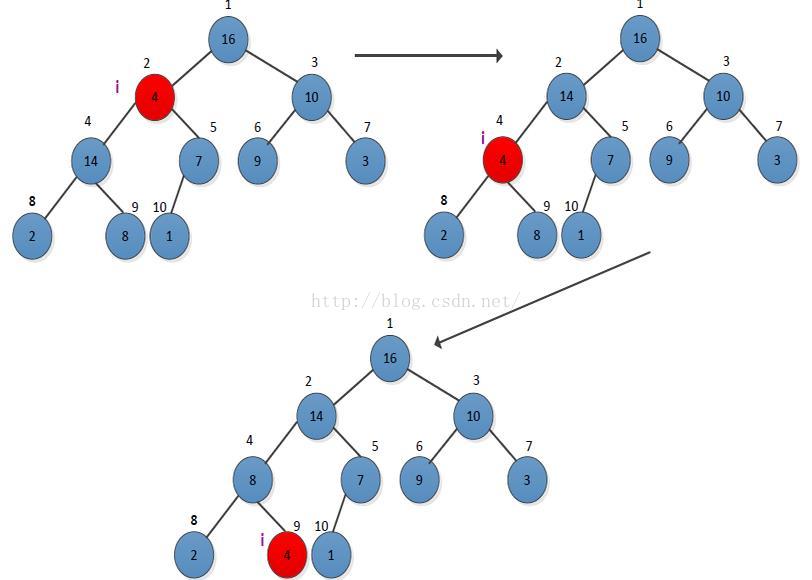
                                                                                     图 2 max_heapify()函数调整i=2位置元素的执行过程

         从上图中可以看出，A[2]违背了最大堆的性质，因为它的值不大于它的孩子，所以需要进行调整。根据教材中max_heapify()的伪代码的代码结构，我进行了C++实现的递归实现，函数max_heapify()的返回值为void：

//维护堆的性质：即使得结点i出左右子树的值小于该节点的值
void max_heapify(int *arr, int length, int i)
{
	int left, right, largest;
	int temp;
	left = LEFT(i);
	right = RIGHT(i);

	if (left <= length && arr[left] > arr[i])
		largest = left;
	else
		largest = i;
	if (right <= length && arr[right] > arr[largest])
		largest = right;
	if (i != largest)
	{
		temp = arr[i];
		arr[i] = arr[largest];
		arr[largest] = temp;

		max_heapify(arr, length, largest);
	}
}

         max_heapify()函数的时间代价包括：

1. 调整A[LEFT(i)]和A[RIGHT(i)]的关系的时间代价：O(1)；
2. 一课棵以i为根节点的子树上运行max_heapify()的时间代价。

       对一个树高为h的结点而言，max_heapify()函数的时间复杂度为：O(h)。

3、建堆

        建堆主要是利用自底向上的方法利用max_heapify()把一个大小为n=A.length的数组A[1.....n ]转换为最大堆。对于叶子节点可以看成是只包含一个元素的堆。

        建堆伪代码：

build_max_heap(A)
1    A.heap_size=A.length
2    for i = A.length/2  downto 1
3         max_heapify(A,i)

        C++代码实现：

//创建堆
void build_max_heap(int *arr, int length)
{
	int i;
	for (i = length / 2; i > 0; i--)
	{
		max_heapify(arr, length, i);
	}
}

        证明build_max_heap()的正确性：

初始化：第一次迭代时：i=length/2，其他节点length/2 +1，length/2 +2，......n都是叶结点。因此节点i=1，......length/2，都是平凡最大堆的根节点。

保持：在for循环中，i的值依次递减，依次建立节点length/2-1，...... ，1的堆结构。

终止：当i=0时，退出for循环。

       每次调用max_heapify()的时间复杂度是O(lgn)，build_max_heap()需要O(n)次这样的调用。因此build_max_heap()总的时间复杂度是：O(nlgn)。

下图是创建堆的过程图：

                        

                                                                                            图3 build_max_heap()操作示意图

4、堆排序算法

 在掌握了max_heapify()函数和build_max_heap()函数的功能后，已经具备了掌握堆排序算法的基础。

 堆排序算法过程：

1. 利用build_max_heap()将数组A[,1......n]建成最大堆，其中n=A.length；
2. 交换A[1]和A[length]的值，使最大元素在堆的最后位置；
3. heap_size = heap_size - 1;  //使堆元素个数减1，即排除最大位置元素到堆外；
4. 调用max_heapify()调整数组A[,1.....heap_size]的结构使之构成新的结构；
5. 重复执行步骤2,——步骤4，知道i=1为止。

伪代码：

HEAPSORT(A)
1  BUILD_MAX_HEAP(A)
2  for i = A.length downto 2
3      exchange A[1] with A[i]
4      A.heap_size = A.heap_size - 1
5      MAX_HEAPIFY(A,1)

C++代码实现：

//堆排序
void heap_sort(int *arr, int length)
{
	int i, temp;
	build_max_heap(arr, length);
	i = length;

	while (i > 1)
	{
		temp = arr[i];
		arr[i] = arr[1];
		arr[1] = temp;
		i--;

		max_heapify(arr, i, 1);
	}
}

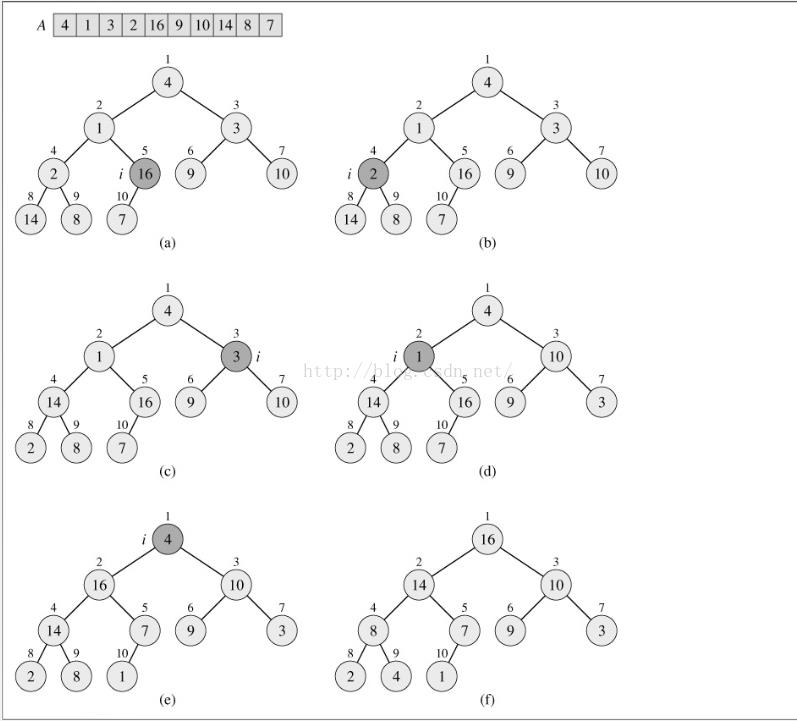
下图显示了HEAPSORT(A)伪代码第2~第5行for循环第一次迭代开始前最大堆的情况和每一次迭代后最大堆的情况：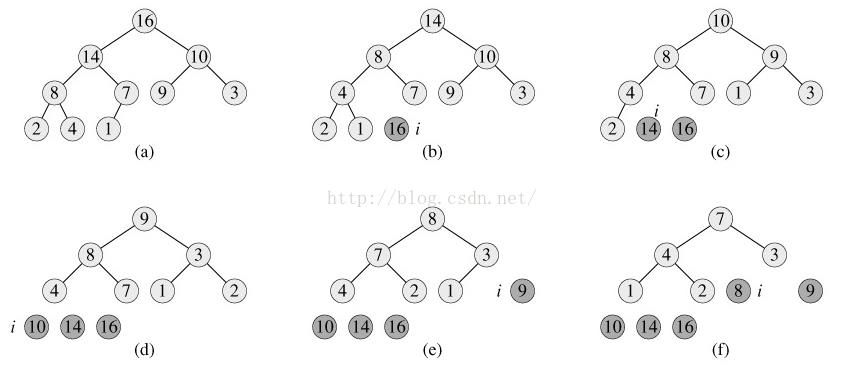

                          

                                                                                              图4  HEAPSOER的运行过程

5、一个简单的例子

        依据本章的知识点，编写的堆排序例子：

#include <iostream>
using namespace std;

#define PARENT(i)  i/2
#define LEFT(i)    i*2
#define RIGHT(i)   i*2+1

//维护堆的性质：即使得结点i出左右子树的值小于该节点的值
void max_heapify(int *arr, int length, int i)
{
	int left, right, largest;
	int temp;
	left = LEFT(i);
	right = RIGHT(i);

	if (left <= length && arr[left] > arr[i])
		largest = left;
	else
		largest = i;
	if (right <= length && arr[right] > arr[largest])
		largest = right;
	if (i != largest)
	{
		temp = arr[i];
		arr[i] = arr[largest];
		arr[largest] = temp;

		max_heapify(arr, length, largest);
	}
}

//创建堆
void build_max_heap(int *arr, int length)
{
	int i;
	for (i = length / 2; i > 0; i--)
	{
		max_heapify(arr, length, i);
	}
}

//堆排序
void heap_sort(int *arr, int length)
{
	int i, temp;
	build_max_heap(arr, length);
	i = length;

	while (i > 1)
	{
		temp = arr[i];
		arr[i] = arr[1];
		arr[1] = temp;
		i--;

		max_heapify(arr, i, 1);
	}
}

int main()
{
	int arr[11] = {NULL, 13, 45, 32, 5, 21, 0, 23, 78, 90, 12};
	cout << "----------------堆排序--------------------" << endl;
	cout << "排序前：";
	for (int i = 1; i < 11; i++)
		cout << arr[i] << "  ";
	cout << endl;
	
	heap_sort(arr, 10);

	cout << "排序后：";
	for (int i = 1; i < 11; i++)
		cout << arr[i] << "  ";
	cout << endl;

	system("pause");
	return 0;
}

程序运行结果：