基于空间直方图meanshift跟踪

Posted 2020-07-02 sunny_develop

最近看了一篇文章《spatiograms versus histograms for region-based tracking》,在此把这篇文章的核心思想及算法推理进行整理。

空间直方图

传统直方图可视为零阶空间直方图，二阶空间直 方图包括直方图每个bin的空间均值和协方差，这种空间信息能获取目标更丰富的特征描述，从而提高了跟踪的鲁棒性。

概率密度函数

空间直方图的空间信息默认服从的是高斯分布，对于两个直方图判断是否相似也是根据多高斯(GMM)的分布特征进行判断的。

高斯分布：即正态分布的概率密度函数均值为μ方差 为σ2 (或标准差σ)是高斯函数的一个实例：

其中σ越小，分布越集中，σ越大，分布越分散。如果一个随机变量X服从这个分布，我们写作 X ~ N(μ,σ2). 如果μ = 0并且σ = 1，这个分布被称为标准正态分布，这个分布能够简化为

多维高斯分布公式：

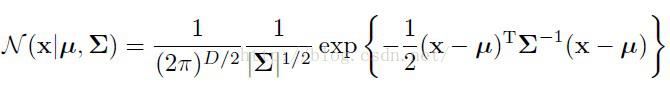
D表示X的维数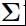，表示D*D的协方差矩阵，定义为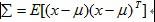

空间直方图与GMMs相似，但GMMs从区域I中得到的多高斯权重和做为相似值，而空间直方图只是从一个高斯分布的区域中获取值。GMMs在它们的区域中是非参数的，它们的范围区间是半参数的，直方图在它们的区域和范围中都是无参数的，空间直方图在它们的范围内是无参数的，但它们的区间是半参数的。

Meanshift

Meanshift算法是基于模式匹配的目标跟踪算法，首先手动选取跟踪窗口，根据颜色直方图分布计算核函数加权下的目标模板，在后续跟踪帧中用相同方法得到选定区域的直方图分布。统计迭代计算，使得每一个点向两个分布相似性最大的方向漂移。

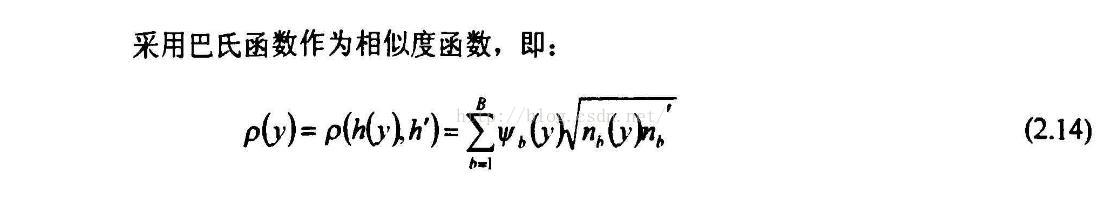
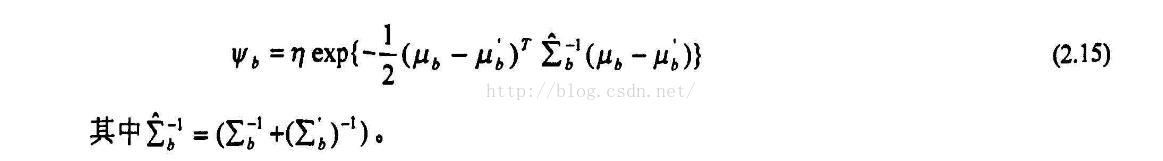
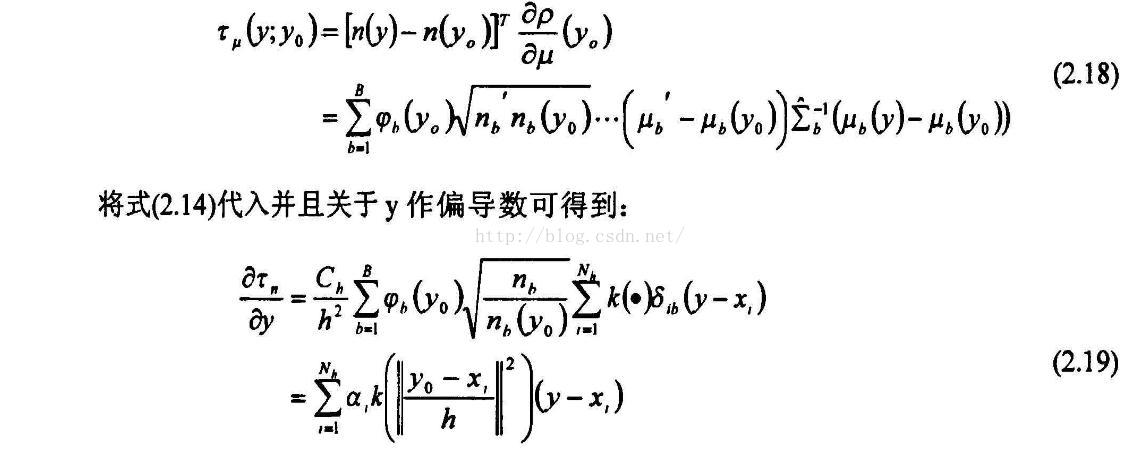
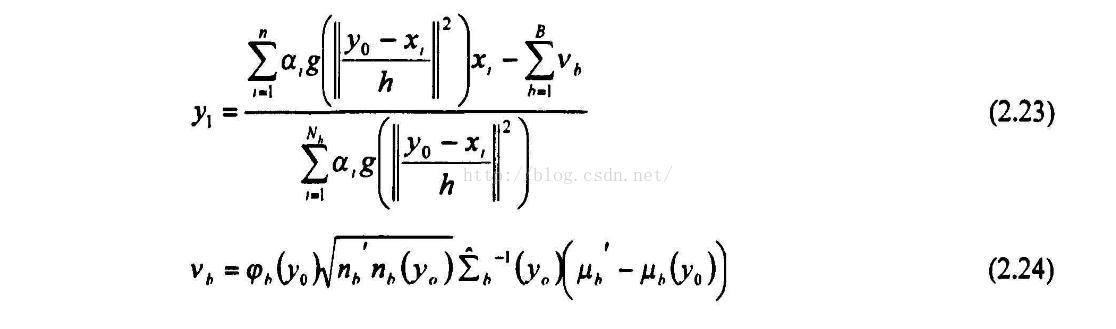
这些就是这篇文章算法的核心思想，之后我会把实现代码贴出来。