决策树的图形可视化
Posted 追寻的鹿
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了决策树的图形可视化相关的知识,希望对你有一定的参考价值。
在Python 中使用 Matplotlib 注释绘制决策树形图
声明:本篇博文是学习《机器学习实战》一书的方式路程,系原创,若转载请标明来源。
上次我们对数据生成决策树有了一定了解,但树是以字典的形式表达的,非常不易于理解;因此,通过决策树的图形可视化有助于我们对决策树的理解和认识。利用强大的Matplotlib 库就可以解决实际的需求。
1 生成决策树的完整的代码
新建一个test.py 文件,用于写决策树的建立代码
1 # coding=utf-8 2 from math import log 3 import operator 4 def calcShannonEnt(dataSet): 5 numEntries = len(dataSet) 6 labelCounts = {} 7 for featVec in dataSet: 8 currentLabel = featVec[-1] # 提取类标号的属性值 9 # 把类标号不同的属性值及其个数存入字典中 10 if currentLabel not in labelCounts .keys(): 11 labelCounts [currentLabel ]=0 12 labelCounts [currentLabel]+=1 13 shannonEnt = 0.0 14 # 计算类标号的平均信息量,如公式中H(S) 15 for key in labelCounts : 16 prob = float(labelCounts [key])/numEntries 17 shannonEnt -= prob * log(prob,2) 18 return shannonEnt 19 20 def createDataSet(): 21 dataSet = [[1, 1, \'yes\'], 22 [1, 1, \'yes\'], 23 [1, 0, \'no\'], 24 [0, 1, \'no\'], 25 [0, 1, \'no\']] 26 labels = [\'no surfacing\',\'flippers\'] 27 #change to discrete values 28 return dataSet, labels 29 def createDataSet1(): 30 dataSet = [[u\'小于等于5\',u\'高\',u\'否\',u\'一般\',u\'否\'], 31 [u\'小于等于5\', u\'高\', u\'否\', u\'好\', u\'否\'], 32 [u\'5到10\', u\'高\', u\'否\', u\'一般\', u\'否\'], 33 [u\'大于等于10\', u\'中\', u\'否\', u\'一般\', u\'是\'], 34 [u\'大于等于10\', u\'低\', u\'是\', u\'一般\', u\'是\'], 35 [u\'5到10\', u\'中\', u\'否\', u\'好\', u\'否\'], 36 [u\'5到10\', u\'高\', u\'是\', u\'一般\', u\'是\'], 37 [u\'小于等于5\', u\'中\', u\'否\', u\'一般\', u\'否\'], 38 [u\'5到10\', u\'中\', u\'否\', u\'好\', u\'否\'], 39 [u\'大于等于10\', u\'高\', u\'是\', u\'好\', u\'是\'], 40 [u\'5到10\', u\'低\', u\'是\', u\'一般\', u\'是\'], 41 [u\'小于等于5\', u\'中\', u\'是\', u\'一般\', u\'是\'], 42 [u\'小于等于5\', u\'低\', u\'是\', u\'一般\', u\'是\'], 43 [u\'大于等于10\', u\'中\', u\'是\', u\'好\', u\'是\']] 44 labels = [u\'役龄\',u\'价格\',u\'是否关键部件\',u\'磨损程度\'] 45 return dataSet ,labels 46 47 # 按照给定特征划分数据集,把符合给定属性值的对象组成新的列表 48 def splitDataSet(dataSet,axis,value): 49 retDataSet = [] 50 for featVec in dataSet: 51 # 选择符合给定属性值的对象 52 if featVec[axis] == value: 53 reduceFeatVec = featVec[:axis] # 对对象的属性值去除给定的特征的属性值 54 reduceFeatVec.extend(featVec[axis+1:]) 55 retDataSet.append(reduceFeatVec ) # 把符合且处理过的对象添加到新的列表中 56 return retDataSet 57 58 # 选取最佳特征的信息增益,并返回其列号 59 def chooseBestFeaturesplit(dataSet): 60 numFeatures = len(dataSet[0])-1 # 获得样本集S 除类标号之外的属性个数,如公式中的k 61 baseEntropy = calcShannonEnt(dataSet) # 获得类标号属性的平均信息量,如公式中H(S) 62 63 bestInfoGain = 0.0 # 对最佳信息增益的初始化 64 bestFeature = -1 # 最佳信息增益的属性在样本集中列号的初始化 65 66 # 对除类标号之外的所有样本属性一一计算其平均信息量 67 for i in range(numFeatures ): 68 featList = [example[i] for example in dataSet] # 提取第i 个特征的所有属性值 69 uniqueVals = set(featList ) # 第i 个特征所有不同属性值的集合,如公式中 aq 70 newEntropy = 0.0 # 对第i 个特征的平均信息量的初始化 71 # 计算第i 个特征的不同属性值的平均信息量,如公式中H(S| Ai) 72 for value in uniqueVals: 73 subDataSet = splitDataSet(dataSet,i,value ) # 提取第i 个特征,其属性值为value的对象集合 74 prob = len (subDataSet )/float(len(dataSet)) # 计算公式中P(Cpq)的概率 75 newEntropy += prob * calcShannonEnt(subDataSet ) # 第i个特征的平均信息量,如 公式中H(S| Ai) 76 infoGain = baseEntropy - newEntropy # 第i 个的信息增益量 77 if (infoGain > bestInfoGain ): # 选取最佳特征的信息增益,并返回其列号 78 bestInfoGain = infoGain 79 80 bestFeature = i 81 return bestFeature 82 83 # 选择列表中重复次数最多的一项 84 def majorityCnt(classList): 85 classCount= {} 86 for vote in classList : 87 if vote not in classCount .keys(): 88 classCount [vote] =0 89 classCount[vote] += 1 90 sortedClassCount = sorted(classCount.iteritems() , 91 key=operator.itemgetter(1), 92 reverse= True ) # 按逆序进行排列,并返回由元组组成元素的列表 93 return sortedClassCount[0][0] 94 95 # 创建决策树 96 def createTree(dataSet,labels): 97 Labels = labels [:] # 防止改变最初的特征列表 98 classList = [example[-1] for example in dataSet ] # 获得样本集中的类标号所有属性值 99 if classList.count(classList [0]) == len(classList): # 类标号的属性值完全相同则停止继续划分 100 return classList[0] 101 if len(dataSet[0]) == 1: # 遍历完所有的特征时,仍然类标号不同的属性值,则返回出现次数最多的属性值 102 return majorityCnt(classList) 103 bestFeat = chooseBestFeaturesplit(dataSet) # 选择划分最佳的特征,返回的是特征在样本集中的列号 104 bestFeatLabel = Labels[bestFeat] # 提取最佳特征的名称 105 myTree = {bestFeatLabel :{}} # 创建一个字典,用于存放决策树 106 del(Labels[bestFeat]) # 从特征列表中删除已经选择的最佳特征 107 featValues = [example[bestFeat] for example in dataSet ] # 提取最佳特征的所有属性值 108 uniqueVals = set(featValues ) # 获得最佳特征的不同的属性值 109 for value in uniqueVals : 110 subLabels = Labels[:] # 把去除最佳特征的特征列表赋值于subLabels 111 myTree [bestFeatLabel][value] = createTree(splitDataSet(dataSet ,bestFeat ,value ), 112 subLabels ) # 递归调用createTree() 113 return myTree 114 115 # 决策树的存储 116 def storeTree(inputTree,filename): 117 import pickle 118 fw = open(filename,\'w\') 119 pickle.dump(inputTree ,fw) 120 fw.close() 121 122 def grabTree(filename): 123 import pickle 124 fr = open(filename) 125 return pickle.load(fr) 126 127 128 # 使用决策树的分类函数 129 def classify(inputTree,featLabels,testVec): 130 firstStr = inputTree.keys()[0] # 获得距离根节点最近的最佳特征 131 secondDict = inputTree[firstStr ] # 最佳特征的分支 132 featIndex = featLabels .index(firstStr) # 获取最佳特征在特征列表中索引号 133 for key in secondDict .keys(): # 遍历分支 134 if testVec [featIndex ] == key: # 确定待查数据和最佳特征的属性值相同的分支 135 if type(secondDict [key]).__name__ == \'dict\': # 判断找出的分支是否是“根节点” 136 classLabel = classify(secondDict[key],featLabels ,testVec) # 利用递归调用查找叶子节点 137 else: 138 classLabel = secondDict [key] # 找出的分支是叶子节点 139 return classLabel
2 决策树的图形可视化
另外新建一个文件 treeplotter.py , 编写决策树图形可视化的代码。
1 # coding=utf-8 2 import matplotlib.pyplot as plt 3 import sys 4 import test 5 reload(sys) 6 sys.setdefaultencoding(\'utf-8\') 7 decisionNode = dict(boxstyle="sawtooth", fc="0.8") 8 leafNode = dict(boxstyle="round4", fc="0.8") 9 arrow_args = dict(arrowstyle="<-") 10 11 # 获得叶子节点的数目 12 def getNumLeafs(myTree): 13 numLeafs = 0 14 firstStr = myTree.keys()[0] 15 secondDict = myTree[firstStr] 16 for key in secondDict.keys(): 17 if type(secondDict[key]).__name__==\'dict\':#test to see if the nodes are dictonaires, if not they are leaf nodes 18 numLeafs += getNumLeafs(secondDict[key]) 19 else: numLeafs +=1 20 return numLeafs 21 22 # 获得决策树的层数 23 def getTreeDepth(myTree): 24 maxDepth = 0 25 firstStr = myTree.keys()[0] 26 secondDict = myTree[firstStr] 27 for key in secondDict.keys(): 28 if type(secondDict[key]).__name__==\'dict\':#test to see if the nodes are dictonaires, if not they are leaf nodes 29 thisDepth = 1 + getTreeDepth(secondDict[key]) 30 else: thisDepth = 1 31 if thisDepth > maxDepth: maxDepth = thisDepth 32 return maxDepth 33 34 def plotNode(nodeTxt, centerPt, parentPt, nodeType): 35 createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords=\'axes fraction\', 36 xytext=centerPt, textcoords=\'axes fraction\', 37 va="center", ha="center", bbox=nodeType, arrowprops=arrow_args ) 38 39 def plotMidText(cntrPt, parentPt, txtString): 40 xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0] 41 yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1] 42 createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30) 43 44 def plotTree(myTree, parentPt, nodeTxt):#if the first key tells you what feat was split on 45 numLeafs = getNumLeafs(myTree) #this determines the x width of this tree 46 depth = getTreeDepth(myTree) 47 firstStr = myTree.keys()[0] #the text label for this node should be this 48 cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff) 49 plotMidText(cntrPt, parentPt, nodeTxt) 50 plotNode(firstStr, cntrPt, parentPt, decisionNode) 51 secondDict = myTree[firstStr] 52 plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD 53 for key in secondDict.keys(): 54 if type(secondDict[key]).__name__==\'dict\':#test to see if the nodes are dictonaires, if not they are leaf nodes 55 plotTree(secondDict[key],cntrPt,str(key)) #recursion 56 else: #it\'s a leaf node print the leaf node 57 plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW 58 plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode) 59 plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key)) 60 plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD 61 #if you do get a dictonary you know it\'s a tree, and the first element will be another dict 62 63 def createPlot(inTree): 64 fig = plt.figure(1, facecolor=\'white\') 65 fig.clf() 66 axprops = dict(xticks=[], yticks=[]) 67 createPlot.ax1 = plt.subplot(111, frameon=False, **axprops) #no ticks 68 #createPlot.ax1 = plt.subplot(111, frameon=False) #ticks for demo puropses 69 plotTree.totalW = float(getNumLeafs(inTree)) 70 plotTree.totalD = float(getTreeDepth(inTree)) 71 plotTree.xOff = -0.5/plotTree.totalW; plotTree.yOff = 1.0; 72 plotTree(inTree, (0.5,1.0), \'\') 73 plt.show() 74 75 76 if __name__ == \'__main__\': 77 dataSet, labels = test.createDataSet1() 78 myTree = test.createTree(dataSet, labels) 79 createPlot(myTree)
3 运行结果显示
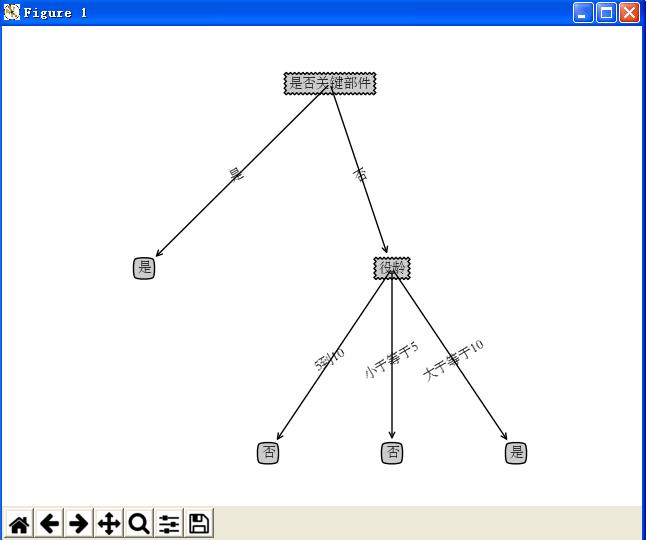
以上是关于决策树的图形可视化的主要内容,如果未能解决你的问题,请参考以下文章
R语言使用party包中的ctree函数构建条件推理决策树(Conditional inference trees)使用plot函数可视化训练好的条件推理决策树条件推理决策树的叶子节点的阴影区域表