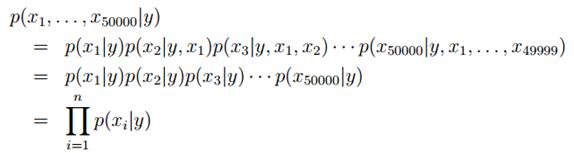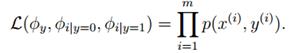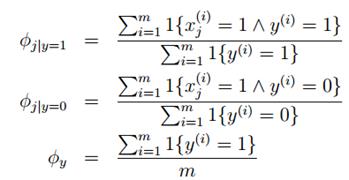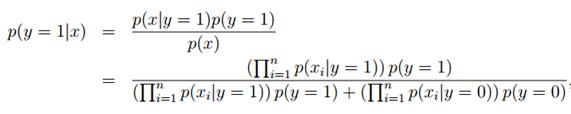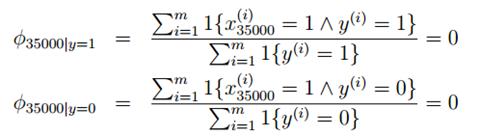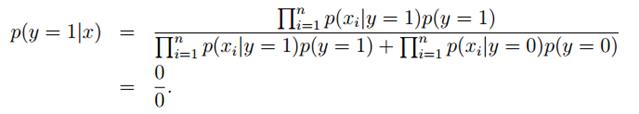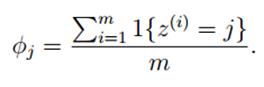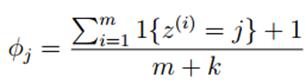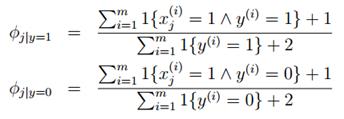生成学习算法(Generative Learning algorithms)

Posted 2020-10-12 迈克老狼2012

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了生成学习算法(Generative Learning algorithms)相关的知识，希望对你有一定的参考价值。

一、引言

前面我们谈论到的算法都是在给定\\(x\\)的情况下直接对\\(p(y|x;\\theta)\\)进行建模。例如，逻辑回归利用\\(h_\\theta(x)=g(\\theta^T x)\\)对\\(p(y|x;\\theta)\\)建模，这类算法称作判别学习算法。

考虑这样一个分类问题，我们根据一些特征来区别动物是大象\\((y=1)\\)还是狗\\((y=0)\\)。给定了这样一个训练集，逻辑回归或感知算法要做的就是去找到一个决策边界，将大象和狗的样本分开来。可以换个思路，首先根据大象的特征来学习出一个大象的模型，然后根据狗的特征学习出狗的模型，对于一个新的样本，提取它的特征先放到大象的模型中求得是大象的概率，然后放到狗的模型中求得是狗的概率，最后我们比较两个概率哪个大，即确定这个动物是哪种类型。也即求\\(p(y|x)=\\frac{p(x|y)p(y)}{p(x)}\\)，\\(y\\)为输出结果，\\(x\\)为特征。

现在我们来定义这两种解决问题的方法：

判别学习算法（discriminative learning algorithm）：直接学习\\(p(y|x)\\)或者是从输入直接映射到输出的方法

生成学习算法（generative learning algorithm）：对\\(p(x|y)\\)(也包括\\(p(y))\\)进行建模。

\\(y\\)为输出变量，值为0或1，如果是大象取1，狗则取0

\\(p(x|y = 0)\\)：对狗的特征进行建模

\\(p(x|y = 1)\\)：对大象的特征建模

对\\(p(x|y)\\)和\\(p(y)\\)完成建模后，运用贝叶斯公式，就可以求得在给定\\(x\\)的情况下\\(y\\)的概率：

\\[p(y|x)=\\frac{p(x|y)p(y)}{p(x)}\\]

\\[p(x) = p(x|y = 1)p(y = 1) + p(x|y =0)p(y = 0)\\]

由于我们关心的是\\(y\\)离散结果中哪一个的概率更大，而不是要求得具体的概率，所以上面的公式我们可以表达为：

\\begin{align*} arg\\,\\underset{y}{max}p(y|x) &=arg\\,\\underset{y}{max}\\frac{p(x|y)p(y)}{p(x)} \\\\
&=arg\\,\\underset{y}{max}p(x|y)p(y) \\end{align*}

\\(arg\\,\\underset{y}{max}p(y|x)\\)的含义：满足条件的最大\\(y\\)值。对\\(y\\)求取最大值，与\\(p(x)\\)无关，所以可以不需要计算\\(p(x)\\)了

常见的生成模型有：隐马尔可夫模型HMM、朴素贝叶斯模型、高斯混合模型GMM、LDA等

二、高斯判别分析(Gaussian Discriminant Analysis)

下面介绍第一个生成学习算法GDA。在GDA中，假设\\(x \\in R^n\\)且是连续的，且\\(p(x|y)\\)满足多项正态分布。

2.1 多项正态分布(The multivariate normal distribution)

假设随机变量\\(X\\)满足\\(n\\)维的多项正态分布，参数为均值向量\\(\\mu\\in R^n\\)，协方差矩阵\\(\\Sigma \\in R^{n\\times n}\\)，记为\\(N(\\mu,\\Sigma)\\)其概率密度表示为：

\\[p(x;\\mu,\\Sigma)=\\frac{1}{(2\\pi)^{n/2}(det\\Sigma)^\\frac{1}{2}}exp\\bigg(-\\frac{1}{2}(x-\\mu)^T\\Sigma^{-1}(x-\\mu)\\bigg)\\]

\\(det\\Sigma\\)表示矩阵\\(\\Sigma\\)的行列式(determinant)。

均值向量：\\(\\mu\\)

协方差矩阵:\\(\\Sigma=E[(X-E[X])(X-E[X])^T]=E[(x-\\mu)(x-\\mu)^T]\\)

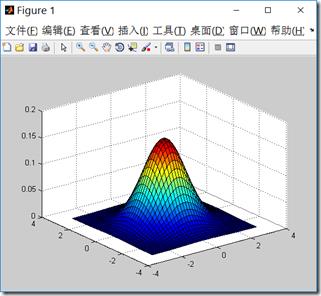
接下来我们用matlab来画一下二维正态分布的图像，我们可以调整均值和协方差矩阵来观察图像。

代码：

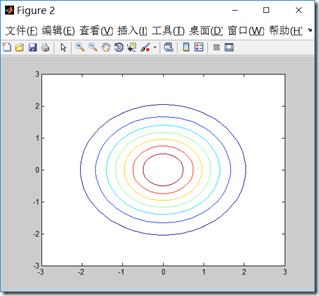
mu=[0 0];
sigma=[1.0 0;0 1.0];
[x y]=meshgrid(linspace(-3,3,40)\',linspace(-3,3,40)\');
X=[x(:) y(:)];
z=mvnpdf(X,mu,sigma);
surf(x,y,reshape(z,40,40));
hold on;
figure;
contour(x,y,reshape(z,40,40));

\\(\\mu\\)决定中心位置，\\(\\Sigma\\)决定投影椭圆的朝向和大小。

2.2高斯判别分析模型(The Gaussian Discriminant Analysis model)

现在有一个分类问题，训练集的特征值\\(x\\)是随机连续值，那么我们可以利用高斯判别分析模型，假设\\(p(x|y)\\)满足多值正态分布，即：

\\[y \\sim Bernoulli(\\phi)\\]

\\[x|y=0 \\sim N(\\mu_0, \\Sigma)\\]

\\[x|y=1 \\sim N(\\mu_1, \\Sigma)\\]

概率分布为：

\\[p(y) = \\phi^y(1-\\phi)^{1-y}\\]

\\[p(x|y=0) = \\frac{1}{(2\\pi)^{n/2}(det\\Sigma)^\\frac{1}{2}}exp\\bigg(-\\frac{1}{2}(x-\\mu_0)^T\\Sigma^{-1}(x-\\mu_0)\\bigg)\\]

\\[p(x|y=1) = \\frac{1}{(2\\pi)^{n/2}(det\\Sigma)^\\frac{1}{2}}exp\\bigg(-\\frac{1}{2}(x-\\mu_1)^T\\Sigma^{-1}(x-\\mu_1)\\bigg)\\]

模型参数为\\(\\phi, \\Sigma, \\mu_0, \\mu_1\\)，对数似然函数为：

\\[l(\\phi,\\mu_0,\\mu_1,\\Sigma)=log\\prod_{i=1}^{m}p(x^{(i)},y^{(i)};\\phi,\\mu_0,\\mu_1,\\Sigma)=log\\prod_{i=1}^{m}p(x^{(i)}|y^{(i)};\\mu_0,\\mu_1,\\Sigma)p(y^{(i)};\\phi)\\]

注意这里的参数有两个\\(\\mu\\)，表示在不同的结果模型下，特征均值不同，但我们假设协方差相同。反映在图上就是不同模型中心位置不同，但形状相同。这样就可以用直线来进行分隔判别。

求得所有的参数：

\\[\\phi = \\frac{1}{m}\\sum\\limits_{i=1}^{m}1\\{y^{(i)}=1\\}\\]

\\[\\mu_0=\\frac{\\sum\\limits_{i=1}^{m}1\\{y^{(i)}=0\\}x^{(i)}}{\\sum\\limits_{i=1}^{m}1\\{y^{(i)}=0\\}}\\]

\\[\\mu_1=\\frac{\\sum\\limits_{i=1}^{m}1\\{y^{(i)}=1\\}x^{(i)}}{\\sum\\limits_{i=1}^{m}1\\{y^{(i)}=1\\}}\\]

\\[\\Sigma = \\frac{1}{m}\\sum\\limits_{i=1}^{m}(x^{(i)}-\\mu_{y{(i)}})(x^{(i)}-\\mu_{y{(i)}})^T\\]

\\(\\phi\\)是训练样本中结果\\(y=1\\)占有的比例。
\\(\\mu_0\\)是\\(y=0\\)的样本中特征均值。
\\(\\mu_1\\)是\\(y=1\\)的样本中特征均值。
\\(\\Sigma\\)是样本特征方差均值。

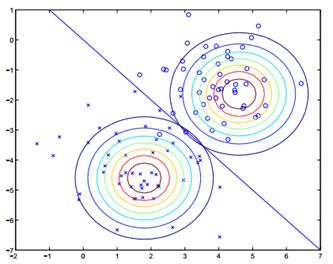
所以通过上面所述，画出图像如下图：

直线两边的\\(y\\)值不同，但协方差矩阵相同，因此形状相同,\\(\\mu\\)不同，因此位置不同。

2.3讨论GDA和逻辑回归(Discussion: GDA and logistic regression)

现在我们把\\(p(y = 1|x; \\phi, \\mu_0, \\mu_1, \\Sigma)\\)看成是\\(x\\)的函数，则可以表达为：

\\[p(y=1|x;\\phi,\\Sigma,\\mu_0,\\mu_1)=\\frac{1}{1+exp(-\\theta^Tx)}\\]

\\(\\theta\\) 是参数\\(\\phi,\\Sigma,\\mu_0,\\mu_1\\)的函数，这正是逻辑回归的形式。

逻辑回归和GDA在训练相同的数据集的时候我们得到两种不同的决策边界，那么怎么样来进行选择模型呢：

上面提到如果\\(p(x|y)\\)是一个多维的高斯分布，那么\\(p(y|x)\\)可以推出一个logistic函数；反之则不一定正确，\\(p(y|x)\\)是一个logistic函数并不能推出\\(p(x|y)\\)服从高斯分布.这说明GDA比logistic回归做了更强的模型假设.

如果\\(p(x|y)\\)真的服从或者趋近于服从高斯分布，则GDA比logistic回归效率高.

当训练样本很大时，严格意义上来说并没有比GDA更好的算法（不管预测的多么精确）.

事实证明即使样本数量很小，GDA相对logisic都是一个更好的算法.

但是，logistic回归做了更弱的假设，相对于不正确的模型假设，具有更好的鲁棒性（robust）.许多不同的假设能够推出logistic函数的形式. 比如说，如果\\(x|y=0 \\sim Poisson(\\lambda_0)\\),\\(x|y=1 \\sim Poisson(\\lambda_1)\\)那么\\(p(y|x)\\)是logistic。

logstic回归在这种类型的Poisson数据中性能很好. 但是如果我们使用GDA模型，把高斯分布应用于并不是高斯数据中，结果是不好预测的，GDA就不是很好了.

三：朴素贝叶斯(Naive Bayes)

在GDA中，特征向量\\(x\\)是连续的实数向量，那么现在谈论一下当\\(x\\)是离散时的情况。

我们沿用对垃圾邮件进行分类的例子，我们要区分邮件是不是垃圾邮件。分类邮件是文本分类的一种应用

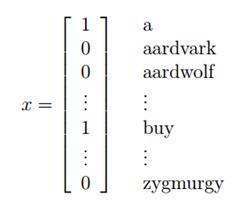
将一封邮件作为输入特征向量，与现有的字典进行比较，如果在字典中第i个词在邮件中出现，则\\(x_i=1\\)，否则\\(x_i=0\\)，所以现在我们假设输入特征向量如下：

选定特征向量后，现在要对\\(p(x|y)\\)进行建模：

假设字典中有50000个词，\\(x \\in \\{0, 1\\}^{50000}\\)如果采用多项式建模，将会有\\(2^{50000}\\)种结果，\\(2^{50000}-1\\)维的参数向量，这样明显参数过多。所以为了对\\(p(x|y)\\)建模，需要做一个强假设，假设\\(x\\)的特征是条件独立的，这个假设称为朴素贝叶斯假设(Naive Bayes (NB) assumption),这个算法就称为朴素贝叶斯分类(Naive Bayes classifier).

解释：
如果有一封垃圾邮件\\((y=1)\\),在邮件中出现buy这个词在2087这个位置,它对39831这个位置是否出现price这个词没有影响，也就是，我们可以这样表达\\(p(x_{2087}|y)=p(x_{2087}|y,x_{39831})\\),这个和\\(x_{2087}\\)和\\(x_{39831}\\)相互独立不同，如果相互独立，则可以写为\\(p(x_{2087})=p(x_{2087}|x_{39831})\\)，我们这里假设的是在给定y的情下，\\(x_{2087}\\)和\\(x_{39831}\\)独立。

现在我们回到问题中，在做出假设后，可以得到：