数据帧CRC32校验算法实现
Posted 没落骑士
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据帧CRC32校验算法实现相关的知识,希望对你有一定的参考价值。
本文设计思想采用明德扬至简设计法。由于本人项目需要进行光纤数据传输,为了保证通信质量要对数据进行校验。在校验算法中,最简单最成熟的非CRC校验莫属了。
得出一个数的CRC校验码还是比较简单的:
- 选定一个CRC生成多项式G(x);
- 将发送数据左移K位,右侧补零(其中K为生成多项式最高次幂);
- 用移位补零后的数据对G(x)进行模2除法(其实就是异或运算);
- 用得到的余数即为该数据的CRC校验码;
发送端将移位补零后数据的低K位0替换成CRC校验码组成新的数据发送出去,接收端对带有校验码的数据对同样的G(x)做模2除法。由于发送端将余数加入在数据尾部,相当于已做了“去余”处理,故若数据传输正确时,接收端的模2除运算余数应为0。其中校验位数和生成多项式不是随便选定的,一般采用常用的标准形式。其中CRCK是指有K为校验位,不同位数对应不同的纠检错能力。之前本人在网上找到一篇关于CRC校验原理的文章,比较详细且浅显易懂:http://mp.weixin.qq.com/s/RNHLZGPD9Ysbxb1FNDn6EA
当刚看完这些资料,对CRC有了大概认识之后,我和很多初学的朋友们一样充满疑惑。CRC如何用硬件实现呢?如何对包含多个数据的数据帧进行校验呢?FCS又是如何在帧尾的下一个时钟周期就得到结果的呢?
最原始的实现方式是采用LFSR(线性反馈移位寄存器)来完成校验功能,以下是结构示意图:

寄存器个数等于G(x)最高次幂,图中gx表示链路通断,与多项式系数相对应:系数为1时连接,0则断开。数据在每个时钟周期从右侧输入1bit,且寄存器内数据右移一位。如此移位,反馈异或的过程即为待发送数据移位后对生成多项式做模2除的过程,故当全部数据位输入完毕,寄存器内部的值即为CRC校验码。我们以较简单的CRC8为例,其G(x) = x^8 + x^2 + x^1 + 1,根据上述分析得到:
reg2(i) = reg1(i-1)^reg7(i-1)^d(i)
reg1(i) = reg0(i-1)^reg7(i-1)^d(i)
reg0(i) = reg7(i-1)^d(i)
regk(i) = regk-1(i-1) (k!=0,1,2)
其中,i表示当前时刻,i-1表示上一时刻。数据位宽定为4bit,经过四个节拍,寄存器内部数据变化过程见表:
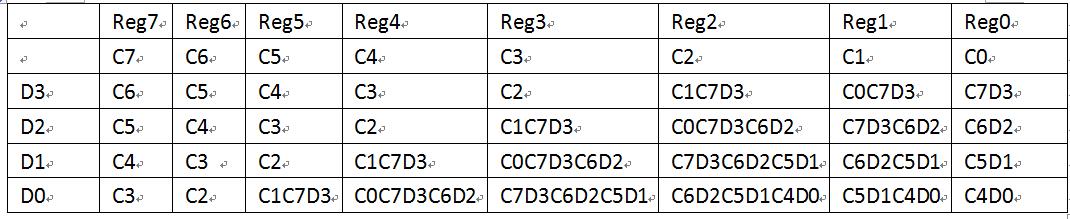
根据上述传递方程推导得出四个节拍后reg7~reg0保存的数值,试想一下:既然每个触发器内保存数值表达式已知,那么如果直接将第四行表达式赋值寄存器,下一个时钟节拍即可得到最终校验结果,而无需等待四个时钟节拍。这就是CRC校验的并行实现方式了!传统的CRC校验算法已经非常成熟,在使用过程中不需要完全自己推导公式,了解基本原理即可。至于代码,有做好的线上生成工具 http://www.easics.com/webtools/crctool 我们选定CRC8,并将数据位宽定义为4bit,验证上述推导过程是否正确。
生成源代码:
1 //////////////////////////////////////////////////////////////////////////////// 2 // Purpose : synthesizable CRC function 3 // * polynomial: x^8 + x^2 + x^1 + 1 4 // * data width: 4 5 //////////////////////////////////////////////////////////////////////////////// 6 module CRC8_D4; 7 8 // polynomial: x^8 + x^2 + x^1 + 1 9 // data width: 4 10 // convention: the first serial bit is D[3] 11 function [7:0] nextCRC8_D4; 12 13 input [3:0] Data; 14 input [7:0] crc; 15 reg [3:0] d; 16 reg [7:0] c; 17 reg [7:0] newcrc; 18 begin 19 d = Data; 20 c = crc; 21 22 newcrc[0] = d[0] ^ c[4]; 23 newcrc[1] = d[1] ^ d[0] ^ c[4] ^ c[5]; 24 newcrc[2] = d[2] ^ d[1] ^ d[0] ^ c[4] ^ c[5] ^ c[6]; 25 newcrc[3] = d[3] ^ d[2] ^ d[1] ^ c[5] ^ c[6] ^ c[7]; 26 newcrc[4] = d[3] ^ d[2] ^ c[0] ^ c[6] ^ c[7]; 27 newcrc[5] = d[3] ^ c[1] ^ c[7]; 28 newcrc[6] = c[2]; 29 newcrc[7] = c[3]; 30 nextCRC8_D4 = newcrc; 31 end 32 endfunction 33 endmodule
代码中公式逻辑部分与表格中第四节拍中寄存器保存的数据一致,证明推导正确。
一个数据的校验大家应该已经掌握了,那如何对整个数据帧进行校验呢?可以看出代码中有data和crc两个数据接口,说明上一个数据的校验结果要作为下一个数据校验过程中移位寄存器的初值,如此循环往复在数据帧的下一拍就能输出整个数据帧的校验值了。关于CRC校验原理和逻辑实现方式已经告一段落。因数据帧校验对校验算法的纠检错能力要求较高,故采用CRC32。这里仅实现检错丢弃功能,即对接收端校验正确的数据帧保留,错误帧丢弃。同样由线上生成工具得到CRC32源代码(数据位宽32bit):
//////////////////////////////////////////////////////////////////////////////// // Purpose : synthesizable CRC function // * polynomial: x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x^1 + 1 // * data width: 32 //////////////////////////////////////////////////////////////////////////////// module CRC32_D32; // polynomial: x^32 + x^26 + x^23 + x^22 + x^16 + x^12 + x^11 + x^10 + x^8 + x^7 + x^5 + x^4 + x^2 + x^1 + 1 // data width: 32 // convention: the first serial bit is D[31] function [31:0] nextCRC32_D32; input [31:0] Data; input [31:0] crc; reg [31:0] d; reg [31:0] c; reg [31:0] newcrc; begin d = Data; c = crc; newcrc[0] = d[31] ^ d[30] ^ d[29] ^ d[28] ^ d[26] ^ d[25] ^ d[24] ^ d[16] ^ d[12] ^ d[10] ^ d[9] ^ d[6] ^ d[0] ^ c[0] ^ c[6] ^ c[9] ^ c[10] ^ c[12] ^ c[16] ^ c[24] ^ c[25] ^ c[26] ^ c[28] ^ c[29] ^ c[30] ^ c[31]; newcrc[1] = d[28] ^ d[27] ^ d[24] ^ d[17] ^ d[16] ^ d[13] ^ d[12] ^ d[11] ^ d[9] ^ d[7] ^ d[6] ^ d[1] ^ d[0] ^ c[0] ^ c[1] ^ c[6] ^ c[7] ^ c[9] ^ c[11] ^ c[12] ^ c[13] ^ c[16] ^ c[17] ^ c[24] ^ c[27] ^ c[28]; newcrc[2] = d[31] ^ d[30] ^ d[26] ^ d[24] ^ d[18] ^ d[17] ^ d[16] ^ d[14] ^ d[13] ^ d[9] ^ d[8] ^ d[7] ^ d[6] ^ d[2] ^ d[1] ^ d[0] ^ c[0] ^ c[1] ^ c[2] ^ c[6] ^ c[7] ^ c[8] ^ c[9] ^ c[13] ^ c[14] ^ c[16] ^ c[17] ^ c[18] ^ c[24] ^ c[26] ^ c[30] ^ c[31]; newcrc[3] = d[31] ^ d[27] ^ d[25] ^ d[19] ^ d[18] ^ d[17] ^ d[15] ^ d[14] ^ d[10] ^ d[9] ^ d[8] ^ d[7] ^ d[3] ^ d[2] ^ d[1] ^ c[1] ^ c[2] ^ c[3] ^ c[7] ^ c[8] ^ c[9] ^ c[10] ^ c[14] ^ c[15] ^ c[17] ^ c[18] ^ c[19] ^ c[25] ^ c[27] ^ c[31]; newcrc[4] = d[31] ^ d[30] ^ d[29] ^ d[25] ^ d[24] ^ d[20] ^ d[19] ^ d[18] ^ d[15] ^ d[12] ^ d[11] ^ d[8] ^ d[6] ^ d[4] ^ d[3] ^ d[2] ^ d[0] ^ c[0] ^ c[2] ^ c[3] ^ c[4] ^ c[6] ^ c[8] ^ c[11] ^ c[12] ^ c[15] ^ c[18] ^ c[19] ^ c[20] ^ c[24] ^ c[25] ^ c[29] ^ c[30] ^ c[31]; newcrc[5] = d[29] ^ d[28] ^ d[24] ^ d[21] ^ d[20] ^ d[19] ^ d[13] ^ d[10] ^ d[7] ^ d[6] ^ d[5] ^ d[4] ^ d[3] ^ d[1] ^ d[0] ^ c[0] ^ c[1] ^ c[3] ^ c[4] ^ c[5] ^ c[6] ^ c[7] ^ c[10] ^ c[13] ^ c[19] ^ c[20] ^ c[21] ^ c[24] ^ c[28] ^ c[29]; newcrc[6] = d[30] ^ d[29] ^ d[25] ^ d[22] ^ d[21] ^ d[20] ^ d[14] ^ d[11] ^ d[8] ^ d[7] ^ d[6] ^ d[5] ^ d[4] ^ d[2] ^ d[1] ^ c[1] ^ c[2] ^ c[4] ^ c[5] ^ c[6] ^ c[7] ^ c[8] ^ c[11] ^ c[14] ^ c[20] ^ c[21] ^ c[22] ^ c[25] ^ c[29] ^ c[30]; newcrc[7] = d[29] ^ d[28] ^ d[25] ^ d[24] ^ d[23] ^ d[22] ^ d[21] ^ d[16] ^ d[15] ^ d[10] ^ d[8] ^ d[7] ^ d[5] ^ d[3] ^ d[2] ^ d[0] ^ c[0] ^ c[2] ^ c[3] ^ c[5] ^ c[7] ^ c[8] ^ c[10] ^ c[15] ^ c[16] ^ c[21] ^ c[22] ^ c[23] ^ c[24] ^ c[25] ^ c[28] ^ c[29]; newcrc[8] = d[31] ^ d[28] ^ d[23] ^ d[22] ^ d[17] ^ d[12] ^ d[11] ^ d[10] ^ d[8] ^ d[4] ^ d[3] ^ d[1] ^ d[0] ^ c[0] ^ c[1] ^ c[3] ^ c[4] ^ c[8] ^ c[10] ^ c[11] ^ c[12] ^ c[17] ^ c[22] ^ c[23] ^ c[28] ^ c[31]; newcrc[9] = d[29] ^ d[24] ^ d[23] ^ d[18] ^ d[13] ^ d[12] ^ d[11] ^ d[9] ^ d[5] ^ d[4] ^ d[2] ^ d[1] ^ c[1] ^ c[2] ^ c[4] ^ c[5] ^ c[9] ^ c[11] ^ c[12] ^ c[13] ^ c[18] ^ c[23] ^ c[24] ^ c[29]; newcrc[10] = d[31] ^ d[29] ^ d[28] ^ d[26] ^ d[19] ^ d[16] ^ d[14] ^ d[13] ^ d[9] ^ d[5] ^ d[3] ^ d[2] ^ d[0] ^ c[0] ^ c[2] ^ c[3] ^ c[5] ^ c[9] ^ c[13] ^ c[14] ^ c[16] ^ c[19] ^ c[26] ^ c[28] ^ c[29] ^ c[31]; newcrc[11] = d[31] ^ d[28] ^ d[27] ^ d[26] ^ d[25] ^ d[24] ^ d[20] ^ d[17] ^ d[16] ^ d[15] ^ d[14] ^ d[12] ^ d[9] ^ d[4] ^ d[3] ^ d[1] ^ d[0] ^ c[0] ^ c[1] ^ c[3] ^ c[4] ^ c[9] ^ c[12] ^ c[14] ^ c[15] ^ c[16] ^ c[17] ^ c[20] ^ c[24] ^ c[25] ^ c[26] ^ c[27] ^ c[28] ^ c[31]; newcrc[12] = d[31] ^ d[30] ^ d[27] ^ d[24] ^ d[21] ^ d[18] ^ d[17] ^ d[15] ^ d[13] ^ d[12] ^ d[9] ^ d[6] ^ d[5] ^ d[4] ^ d[2] ^ d[1] ^ d[0] ^ c[0] ^ c[1] ^ c[2] ^ c[4] ^ c[5] ^ c[6] ^ c[9] ^ c[12] ^ c[13] ^ c[15] ^ c[17] ^ c[18] ^ c[21] ^ c[24] ^ c[27] ^ c[30] ^ c[31]; newcrc[13] = d[31] ^ d[28] ^ d[25] ^ d[22] ^ d[19] ^ d[18] ^ d[16] ^ d[14] ^ d[13] ^ d[10] ^ d[7] ^ d[6] ^ d[5] ^ d[3] ^ d[2] ^ d[1] ^ c[1] ^ c[2] ^ c[3] ^ c[5] ^ c[6] ^ c[7] ^ c[10] ^ c[13] ^ c[14] ^ c[16] ^ c[18] ^ c[19] ^ c[22] ^ c[25] ^ c[28] ^ c[31]; newcrc[14] = d[29] ^ d[26] ^ d[23] ^ d[20] ^ d[19] ^ d[17] ^ d[15] ^ d[14] ^ d[11] ^ d[8] ^ d[7] ^ d[6] ^ d[4] ^ d[3] ^ d[2] ^ c[2] ^ c[3] ^ c[4] ^ c[6] ^ c[7] ^ c[8] ^ c[11] ^ c[14] ^ c[15] ^ c[17] ^ c[19] ^ c[20] ^ c[23] ^ c[26] ^ c[29]; newcrc[15] = d[30] ^ d[27] ^ d[24] ^ d[21] ^ d[20] ^ d[18] ^ d[16] ^ d[15] ^ d[12] ^ d[9] ^ d[8] ^ d[7] ^ d[5] ^ d[4] ^ d[3] ^ c[3] ^ c[4] ^ c[5] ^ c[7] ^ c[8] ^ c[9] ^ c[12] ^ c[15] ^ c[16] ^ c[18] ^ c[20] ^ c[21] ^ c[24] ^ c[27] ^ c[30]; newcrc[16] = d[30] ^ d[29] ^ d[26] ^ d[24] ^ d[22] ^ d[21] ^ d[19] ^ d[17] ^ d[13] ^ d[12] ^ d[8] ^ d[5] ^ d[4] ^ d[0] ^ c[0] ^ c[4] ^ c[5] ^ c[8] ^ c[12] ^ c[13] ^ c[17] ^ c[19] ^ c[21] ^ c[22] ^ c[24] ^ c[26] ^ c[29] ^ c[30]; newcrc[17] = d[31] ^ d[30] ^ d[27] ^ d[25] ^ d[23] ^ d[22] ^ d[20] ^ d[18] ^ d[14] ^ d[13] ^ d[9] ^ d[6] ^ d[5] ^ d[1] ^ c[1] ^ c[5] ^ c[6] ^ c[9] ^ c[13] ^ c[14] ^ c[18] ^ c[20] ^ c[22] ^ c[23] ^ c[25] ^ c[27] ^ c[30] ^ c[31]; newcrc[18] = d[31] ^ d[28] ^ d[26] ^ d[24] ^ d[23] ^ d[21] ^ d[19] ^ d[15] ^ d[14] ^ d[10] ^ d[7] ^ d[6] ^ d[2] ^ c[2] ^ c[6] ^ c[7] ^ c[10] ^ c[14] ^ c[15] ^ c[19] ^ c[21] ^ c[23] ^ c[24] ^ c[26] ^ c[28] ^ c[31]; newcrc[19] = d[29] ^ d[27] ^ d[25] ^ d[24] ^ d[22] ^ d[20] ^ d[16] ^ d[15] ^ d[11] ^ d[8] ^ d[7] ^ d[3] ^ c[3] ^ c[7] ^ c[8] ^ c[11] ^ c[15] ^ c[16] ^ c[20] ^ c[22] ^ c[24] ^ c[25] ^ c[27] ^ c[29]; newcrc[20] = d[30] ^ d[28] ^ d[26] ^ d[25] ^ d[23] ^ d[21] ^ d[17] ^ d[16] ^ d[12] ^ d[9] ^ d[8] ^ d[4] ^ c[4] ^ c[8] ^ c[9] ^ c[12] ^ c[16] ^ c[17] ^ c[21] ^ c[23] ^ c[25] ^ c[26] ^ c[28] ^ c[30]; newcrc[21] = d[31] ^ d[29] ^ d[27] ^ d[26] ^ d[24] ^ d[22] ^ d[18] ^ d[17] ^ d[13] ^ d[10] ^ d[9] ^ d[5] ^ c[5] ^ c[9] ^ c[10] ^ c[13] ^ c[17] ^ c[18] ^ c[22] ^ c[24] ^ c[26] ^ c[27] ^ c[29] ^ c[31]; newcrc[22] = d[31] ^ d[29] ^ d[27] ^ d[26] ^ d[24] ^ d[23] ^ d[19] ^ d[18] ^ d[16] ^ d[14] ^ d[12] ^ d[11] ^ d[9] ^ d[0] ^ c[0] ^ c[9] ^ c[11] ^ c[12] ^ c[14] ^ c[16] ^ c[18] ^ c[19] ^ c[23] ^ c[24] ^ c[26] ^ c[27] ^ c[29] ^ c[31]; newcrc[23] = d[31] ^ d[29] ^ d[27] ^ d[26] ^ d[20] ^ d[19] ^ d[17] ^ d[16] ^ d[15] ^ d[13] ^ d[9] ^ d[6] ^ d[1] ^ d[0] ^ c[0] ^ c[1] ^ c[6] ^ c[9] ^ c[13] ^ c[15] ^ c[16] ^ c[17] ^ c[19] ^ c[20] ^ c[26] ^ c[27] ^ c[29] ^ c[31]; newcrc[24] = d[30] ^ d[28] ^ d[27] ^ d[21] ^ d[20] ^ d[18] ^ d[17] ^ d[16] ^ d[14] ^ d[10] ^ d[7] ^ d[2] ^ d[1] ^ c[1] ^ c[2] ^ c[7] ^ c[10] ^ c[14] ^ c[16] ^ c[17] ^ c[18] ^ c[20] ^ c[21] ^ c[27] ^ c[28] ^ c[30]; newcrc[25] = d[31] ^ d[29] ^ d[28] ^ d[22] ^ d[21] ^ d[19] ^ d[18] ^ d[17] ^ d[15] ^ d[11] ^ d[8] ^ d[3] ^ d[2] ^ c[2] ^ c[3] ^ c[8] ^ c[11] ^ c[15] ^ c[17] ^ c[18] ^ c[19] ^ c[21] ^ c[22] ^ c[28] ^ c[29] ^ c[31]; newcrc[26] = d[31] ^ d[28] ^ d[26] ^ d[25] ^ d[24] ^ d[23] ^ d[22] ^ d[20] ^ d[19] ^ d[18] ^ d[10] ^ d[6] ^ d[4] ^ d[3] ^ d[0] ^ c[0] ^ c[3] ^ c[4] ^ c[6] ^ c[10] ^ c[18] ^ c[19] ^ c[20] ^ c[22] ^ c[23] ^ c[24] ^ c[25] ^ c[26] ^ c[28] ^ c[31]; newcrc[27] = d[29] ^ d[27] ^ d[26] ^ d[25] ^ d[24] ^ d[23] ^ d[21] ^ d[20] ^ d[19] ^ d[11] ^ d[7] ^ d[5] ^ d[4] ^ d[1] ^ c[1] ^ c[4] ^ c[5] ^ c[7] ^ c[11] ^ c[19] ^ c[20] ^ c[21] ^ c[23] ^ c[24] ^ c[25] ^ c[26] ^ c[27] ^ c[29]; newcrc[28] = d[30] ^ d[28] ^ d[27] ^ d[26] ^ d[25] ^ d[24] ^ d[22] ^ d[21] ^ d[20] ^ d[12] ^ d[8] ^ d[6] ^ d[5] ^ d[2] ^ c[2] ^ c[5] ^ c[6] ^ c[8] ^ c[12] ^ c[20] ^ c[21] ^ c[22] ^ c[24] ^ c[25] ^ c[26] ^ c[27] ^ c[28] ^ c[30]; newcrc[