二项式分布预测新生儿

Posted 2020-10-11

医院每天都有新生儿呱呱落地。每天会有多少男婴出生，多少女婴出生呢？这个问题不难，我们可以用二项式分布来计算，python建模观察。

二项分布即重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。

程序调用了python的numpy,scipy两个模块。numpy用于矩阵运算；scipy是numpy的高级版本，用于更高级的自然科学应用，例如信号处理，傅里叶分析。

我们假设医院每天100婴儿出生 ， num代表每天婴儿出生总数。然后假设男孩出生概率为0.5，p代表男孩出生概率 。

num=100

p=0.5

运行环境：win7_32位，anaconda 2（python2.7）

源码放在文章末尾，所有代码经本人测试没有问题。

写好脚本后运行

放大console控制台观察

 

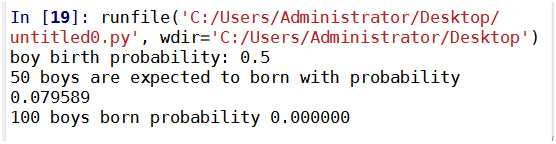
程序自动预测医院每天出生100个新生儿，有50个男孩出生。这里解释一下， 50个男孩出生并不一定发生，只是概率最大。医院每天出生100个新生儿，有可能出生40个男孩，或30个男孩，或10个男孩，只是这些可能性并不高。假设我们想知道医院每天出生100个新生儿中全部是男孩概率。程序变量x代表出生男孩数量，Get_probability_x(x)函数计算其概率。

x=100

x_probability=Get_probability_x(x) 

控制台最后一行显示所有新生儿都为男婴的概率几乎为0.

list_probablity是各种情况的概率列表

 

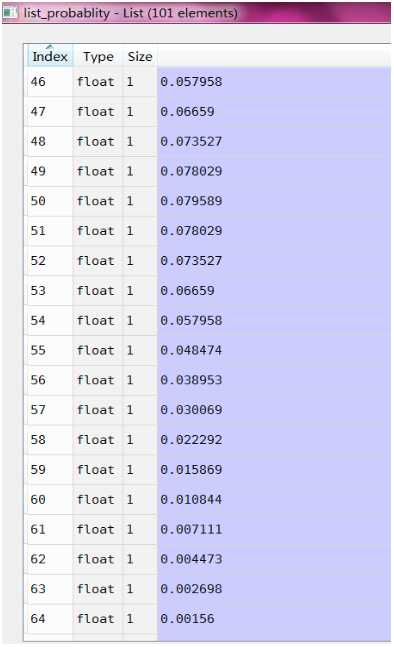
总结一下，二项式期望值公式E(X)=E[X(1)+X(2)+X(3)....X(n)]=np。二项式期望值通俗的讲就是数量乘以概率。通过程序建模，我们清楚认识到期望值只是一种最大概率的可能，并不代表一定会发生。

代码运行问题反馈邮箱[email protected]

源码：

# -*- coding: utf-8 -*-

from scipy import stats

import numpy as np

#返回各种可能的概率列表

def Get_list_probability(num,p,array_x):

    binoDist=stats.binom(num,p)

    array_probability=binoDist.pmf(array_x)

    list_probablity=list(array_probability)

    list_probablity1=[round(i,6) for i in list_probablity]

    return list_probablity1

#二项式函数的最大概率值和第几次出现，num为试验次数，p为概率

def Max_BinomialDistribution(list_probablity,array_x):

    maxProbability=max(list_probablity)

    #概率最大值所在索引

    index=list_probablity.index(maxProbability)

    #第几次试验概率最大

    x=array_x[index]

    return maxProbability,x

#测试X次成功概率

def Get_probability_x(x):

    value=round(list_probablity[x],2)

    return value

def Print():

    print "boy birth probability:",p

print "%d boys are expected to born with probability %f"%(maxProbability[1],maxProbability[0])

    print "%d boys born probability %f"%(x,x_probability)

#医院每天100人出生   

num=100

#男孩出生概率

p=0.5

array_x=np.arange(101)

list_probablity=Get_list_probability(num,p,array_x)

#得到最大概率及其对应x试验次数

maxProbability=Max_BinomialDistribution(list_probablity,array_x)

# X个男孩出生概率预测

x=100

x_probability=Get_probability_x(x)

Print()

End.