北大高代考研题解答

Posted 2020-10-11 Eufisky

正十二面体有$12$个面,每个面为正五边形,每个顶点连接$3$条棱.求它的内切球与外接球半径比.

---

 

解.不妨设正十二面体的棱长均为$a$.

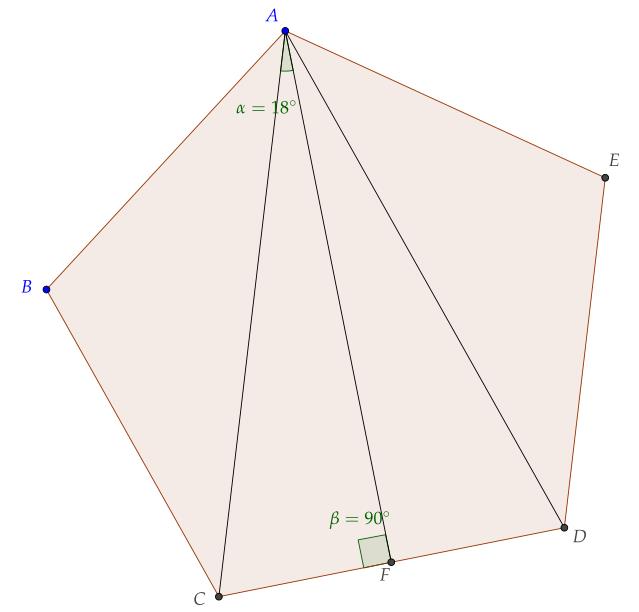
先求正五边形的高.如图所示,这里的字母记号和下图有冲突,请注意区别.利用这么个事实,从正五边形某个顶点向两个对点连线,这两条线将会三等分内角$\\displaystyle \\frac{(5-2)\\times 180^\\circ}5=108^\\circ$,则三等分后的角$\\angle CAD=36^\\circ$,则$\\angle CAF=18^\\circ$,因此正五边形的高为
$$
h=\\frac{a/2}{\\tan 18^{\\circ}}=\\frac{a/2}{\\tan \\left( \\pi /10 \\right)}=\\frac{1}{2}\\sqrt{5+2\\sqrt{5}}a.
$$

接着求正十二面体的二面角,记某顶点处的三条等长的棱形成的向量分别为$\\vec{a},\\vec{b},\\vec{c}$,其中的任意两个向量夹角为$108^\\circ$.

事实上,利用Lagrange恒等式$$\\left(\\overrightarrow{a}\\times\\overrightarrow{b}\\right)\\cdot\\left(\\overrightarrow{c}\\times\\overrightarrow{d}\\right)=\\left|\\begin{matrix}\\overrightarrow{a}\\cdot\\overrightarrow{c}& \\overrightarrow{a}\\cdot\\overrightarrow{d}\\\\\\overrightarrow{b}\\cdot\\overrightarrow{c}& \\overrightarrow{b}\\cdot\\overrightarrow{d}\\\\\\end{matrix}\\right|,$$我们有
\\begin{align*}
\\frac{\\left( \\overrightarrow{a}\\times \\overrightarrow{b} \\right) \\cdot \\left( \\overrightarrow{b}\\times \\overrightarrow{c} \\right)}{\\left| \\overrightarrow{a}\\times \\overrightarrow{b} \\right|\\left| \\overrightarrow{b}\\times \\overrightarrow{c} \\right|}&=\\frac{1}{\\left| \\overrightarrow{a}\\times \\overrightarrow{b} \\right|\\left| \\overrightarrow{b}\\times \\overrightarrow{c} \\right|}\\left| \\begin{matrix}
\\overrightarrow{a}\\cdot \\overrightarrow{b}& \\overrightarrow{a}\\cdot \\overrightarrow{c}\\\\
\\overrightarrow{b}\\cdot \\overrightarrow{b}& \\overrightarrow{b}\\cdot \\overrightarrow{c}\\\\
\\end{matrix} \\right|\\\\
&=\\frac{1}{a^4\\sin 108^{\\circ}}\\left| \\begin{matrix}
a^2\\cos 108^{\\circ}& a^2\\cos 108^{\\circ}\\\\
a^2& a^2\\cos 108^{\\circ}\\\\
\\end{matrix} \\right|\\\\
&=\\frac{\\cos ^2108^{\\circ}-\\cos 108^{\\circ}}{\\sin 108^{\\circ}}=\\frac{1}{\\sqrt{5}},
\\end{align*}
这里利用了
$$
\\cos 108^{\\circ}=\\frac{1-\\sqrt{5}}{4},\\qquad \\sin 108^{\\circ}=\\sqrt{\\frac{5+\\sqrt{5}}{8}}.
$$
由正十二面体实物图可以看出二面角显然为钝角,因此所求二面角$\\theta$的余弦值为$\\displaystyle \\frac{1}{\\sqrt{5}}$.

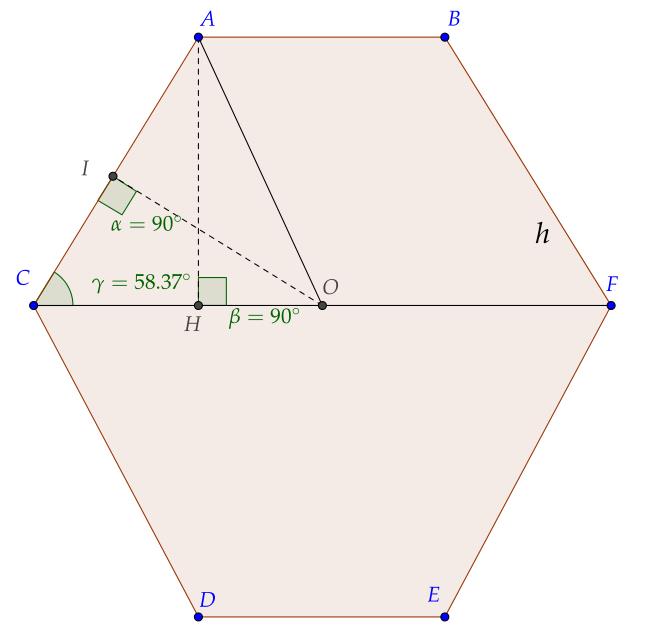
这题关键是找到适合计算的截面图,因为建坐标系比较复杂,利用坐标系不太现实.不过在英文Wiki上有这些坐标参数,利用这些数据此问题瞬间得到解答.如图便是我们找到的可行截面图,也就是$AC=h=\\frac{1}{2}\\sqrt{5+2\\sqrt{5}}a$,且$\\angle ACO=\\gamma=\\theta/2$.我们有
$$
\\cos \\theta =-\\frac{1}{\\sqrt{5}}=1-2\\sin ^2\\gamma \\Rightarrow \\sin \\gamma =\\sqrt{\\frac{5+\\sqrt{5}}{10}},\\cos \\gamma =\\sqrt{\\frac{5-\\sqrt{5}}{10}}.
$$
因此梯形的下底为
\\begin{align*}
CF&=2CH+a=2h\\cos \\gamma +a\\\\
&=2\\times \\frac{1}{2}\\sqrt{5+2\\sqrt{5}}a\\times \\sqrt{\\frac{5-\\sqrt{5}}{10}}+a=\\frac{3+\\sqrt{5}}{2}a.
\\end{align*}
由此得
$$
r=OI=\\frac{CF}{2}\\sin \\gamma =\\frac{3+\\sqrt{5}}{4}a\\times \\sqrt{\\frac{5+\\sqrt{5}}{10}}=\\frac{1}{2}\\sqrt{\\frac{25+11\\sqrt{5}}{10}}a,
$$
而由余弦定理可知
\\begin{align*}
R^2&=OA^2=h^2+\\left( \\frac{CF}{2} \\right) ^2-2h\\cdot \\frac{CF}{2}\\cdot \\cos \\gamma\\\\
&=\\left( \\frac{1}{2}\\sqrt{5+2\\sqrt{5}}a \\right) ^2+\\left( \\frac{3+\\sqrt{5}}{4}a \\right) ^2-\\sqrt{5+2\\sqrt{5}}\\times \\frac{3+\\sqrt{5}}{4}a\\times \\sqrt{\\frac{5-\\sqrt{5}}{10}}\\\\
&=\\frac{9+3\\sqrt{5}}{8}a^2,
\\end{align*}
即$$
R=\\frac{\\sqrt{3}+\\sqrt{15}}{4}a,
$$
从而所求内切球与外接球半径比等于
$$
\\frac{r}{R}=\\frac{\\frac{1}{2}\\sqrt{\\frac{25+11\\sqrt{5}}{10}}a}{\\frac{\\sqrt{3}+\\sqrt{15}}{4}a}=\\sqrt{\\frac{5+2\\sqrt{5}}{15}}.
$$
注:其实一开始我把$-\\frac1{\\sqrt{5}}$的负号丢了,折腾了半天.此外,我们还可以计算出正十二面体的表面积$S$和体积$V$分别为
$$
S=3\\sqrt{25+10\\sqrt{5}}a^2,\\qquad V=\\frac{15+7\\sqrt{5}}{4}a^3.
$$