小X的佛光 NOIP模拟赛 倍增LCA 树结构

Posted 2020-10-11 JayWang

题面与官方std详解在最下方。

题意：给出一颗N个节点、N-1条边的无向图（树），给出Q个询问，每个询问有两条路径，求路径覆盖点的个数。其中N_max=Q_max=200000

思路：

对于在树上的路径，我们可以用LCA解决。

举个栗子，若A与B结点的LCA是C，那么L_AB=L_AC+L_BC。当边权都是1的时候，这个式子又可以化为：L_AB=C_dep-A_dep+C_dep-B_dep，读者可以自行画图验证。

怎么用？

对于两条给定路径，求公共部分的结点数，既可以转化为求公共部分的边数+1。

那么对于题目给出的两条确定路径AB、BC，可以知道公共结点数=(L_AB+L_BC-L_AC)/2+1，读者可以自行画图验证。

这就好办了，只需要写一个树上倍增求LCA即可。

其他需要注意的事情

本题N_max=200000，如果用dfs求深度和父亲节点，会爆栈。

怎么解决？

1、换用bfs求解上述参数。

2、扩栈（在编译器参数后面加上-Wl,--stack=256000000）（意思是把栈扩展到256MB）

AC代码

 1 #include<cstdio>
 2 #include<cstring>
 3 #include<algorithm>
 4 using namespace std;
 5 template<class T> inline void read(T &_a){
 6     bool f=0;int _ch=getchar();_a=0;
 7     while(_ch<\'0\' || _ch>\'9\'){if(_ch==\'-\')f=1;_ch=getchar();}
 8     while(_ch>=\'0\' && _ch<=\'9\'){_a=(_a<<1)+(_a<<3)+_ch-\'0\';_ch=getchar();}
 9     if(f)_a=-_a;
10 }
11 
12 const int maxn=200001;
13 struct edge
14 {
15     int to,next;
16 }w[maxn<<1];
17 int n,Q,num,egcnt,head[maxn],fa[maxn][20],ans,dep[maxn];
18 bool vis[maxn];
19 
20 inline void __SUPER_addedge(int from,int to)
21 {
22     w[++egcnt].to=to;
23     w[egcnt].next=head[from];
24     head[from]=egcnt;
25     w[++egcnt].to=from;
26     w[egcnt].next=head[to];
27     head[to]=egcnt;
28 }
29 
30 void rushA(int u,int fr)
31 {
32     fa[u][0]=fr; dep[u]=dep[fr]+1;
33     for (register int i=head[u];i;i=w[i].next) if(w[i].to!=fr) rushA(w[i].to,u);
34 }
35 
36 inline void rushB()
37 {
38     for (register int i=1;i<=19;++i)
39         for (register int v=1;v<=n;++v)
40             fa[v][i]=fa[fa[v][i-1]][i-1];
41 }
42 
43 inline int LCA(int a,int b)
44 {
45     if(dep[a]<dep[b]) swap(a,b);
46     for (register int i=19;i>=0&&dep[a]>dep[b];--i)
47         if(dep[a]-(1<<i)>=dep[b]) a=fa[a][i];
48     for (register int i=19;i>=0;--i)
49         if(fa[a][i]!=fa[b][i]) a=fa[a][i],b=fa[b][i];
50     return a==b?a:fa[a][0];
51 }
52 
53 int main()
54 {
55     freopen("light.in","r",stdin);
56     freopen("light.out","w",stdout);
57     read(n); read(Q); read(num);
58     for (register int i=1,x,y;i<n;++i) read(x),read(y),__SUPER_addedge(x,y);
59     rushA(1,0); rushB();
60     for (register int a,b,c;Q;--Q)
61     {
62         read(a); read(b); read(c);
63         int l1=LCA(a,b),l2=LCA(b,c),l3=LCA(a,c);
64         int s1=dep[a]-dep[l1]+dep[b]-dep[l1];
65         int s2=dep[b]-dep[l2]+dep[c]-dep[l2];
66         int s3=dep[a]-dep[l3]+dep[c]-dep[l3];
67         printf("%d\\n",(s1+s2-s3)/2+1);
68     }
69     return 0;
70 }

ViewCode

 

小X是远近闻名的学佛，平日里最喜欢做的事就是蒸发学水。

小X所在的城市X城是一个含有N个节点的无向图，同时，由于X国是一个发展中国家，为了节约城市建设的经费，X国首相在建造X城时只建造N–1条边，使得城市的各个地点能够相互到达。

小X计划蒸发Q天的学水，每一天会有一名学水从A地走到B地，并在沿途各个地点留下一个水塘。此后，小X会从C地走到B地，并用佛光蒸发沿途的水塘。由于X城是一个学佛横行的城市，学水留下的水塘即使没有被小X蒸发，也会在第二天之前被其他学佛蒸发殆尽。

现在，小X想要知道，他每一天能够蒸发多少水塘呢?

输入格式

第一行三个整数N,Q,num，分别表示X城地点的个数，小X蒸发学水的天数，以及测试点编号。注意，测试点编号是为了让选手们更方便的获得部分分，你可能不需要用到这则信息，在下发的样例中，测试点编号的含义是该样例满足某一测试点限制。

接下来N–1行，每行两个整数X,Y，表示X地与Y地之间有一条边。

接下来Q行，每行三个整数A,B,C，表示一天中，有一名学水从A地走到B地，而小X会从C地走到B地。

输出格式

输出Q行，每行一个整数，表示小X能够蒸发的水塘数。

样例输入

331

12

23

123

113

313

样例输出

1

1

3

数据规模与约定

特殊性质1：第i条边连接第i和第i+1个地点。

特殊性质2：A=C。

 

官方STD题解：

注意到问题实际上是问树上一个点到另外两点路径的重合长度，也就是说，这两条路径有一个端点是重合的，不妨就此性质构建算法。

 

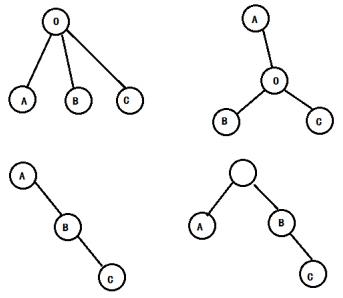
树上三点，或是呈一条链的形式，或是存在一个中心，使得中心到三点之间的路径不相交。如下图，上方的两种情况是A、B、C点存在中心O，下方两种情况是A、B、C点在一条链上。对于呈一条链的形式，我们不妨将三个点中，位于中间的那个点称为三个点的中心，如此一来，我们要求的答案实际上是中心到B点的距离。那么，如何求中心呢？通过观察上图，我们发现，中心一定是A、B、C点中两点的LCA。并且，通过进一步观察，我们可以发现，中心是A、B、C点两两的LCA中，深度最大的点。所以，我们只需求出中心，在求出中心到B点的距离即可解决本题。该算法的时间复杂度是O（N+Q）或O（（N+Q）*LogN）的。