[51nod] 1040 最大公约数之和

Posted 2020-10-11 Lev今天学习了吗

1040 最大公约数之和

题目来源： rihkddd 基准时间限制：1 秒 空间限制：131072 KB 分值: 80 难度：5级算法题

 

给出一个n，求1-n这n个数，同n的最大公约数的和。比如：n = 6

1,2,3,4,5,6 同6的最大公约数分别为1,2,3,2,1,6，加在一起 = 15

 

Input

1个数N(N <= 10^9)

Output

公约数之和

Input示例

6

Output示例

15

Analysis分析

这道题思考题

结论：

　　　　　　　　

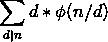
为什么呢？

主要思路：枚举最大公约数，然后求出同个最大公约数的数字的数量

然后把这些加起来就行了

最后需要额外加上 1 和 n 的情况

那么对于每个最大公约数，只要除去这个最大公约数，那么数 a 和 n 就互质了

因此这个数量就是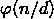 

那么对于每一个 n 的因数，我们都这么叠加一下就行。

Code代码

 1 #include<cstdio>
 2 #include<iostream>
 3 #define LL long long
 4 using namespace std;
 5 
 6 LL x;
 7 
 8 LL euler(LL x){
 9     LL ans = 1;
10     for(LL i = 2;i*i <= x;i++){
11         if(x%i) continue;
12         ans *= i-1;
13         x /= i;
14         while(x%i == 0){
15             ans *= i;
16             x /= i;
17         }
18     }if(x > 1) ans *= x-1;
19     return ans;
20 }
21 
22 int main(){
23     scanf("%I64d",&x);
24 
25     LL tot = 0;
26 
27     for(int i = 1;i*i <= x;i++){
28         if(x%i) continue;
29         LL t = x/i;
30         tot += i*euler(t);    
31         if(i != t) tot += t*euler(x/t);
32     }cout << tot;
33     
34     return 0;
35 }

qwq 欧拉函数你好啊