机器学习-梯度下降参数调优小结

Posted 2020-10-11 柯君的博客

在机器学习领域，通过对特征的参数调优可以让模型的预测值更接近真实值的常见的两种方法包括最小二乘法和梯度下降方法。目前梯度下降更成为了一种解决问题的方法和思路，在集成学习和深度学习领域都有较多的应用。

在机器学习领域，通过对特征的参数调优可以让模型的预测值更接近真实值的常见的两种方法包括最小二乘法和梯度下降方法。目前梯度下降更成为了一种解决问题的方法和思路，在集成学习和深度学习领域都有较多的应用。

定义

直观理解“梯度下降”：我们在山上想要下山的时候，不知道方向，手头上只有一个仪器可以提醒当前的海拔，这时候随意的走一步可以知道海拔变大还是变小，往海拔变小的方向一步一步走，通过顺着梯度下降的方向一步步缩小海拔，直到海拔也基本没有变化为止，这样我们就从山顶走道山下。这就是梯度下降的一个运算思维。在实际的机器学习中，山顶的海拔高度代表了模型的预测值和真实值之间的差距，而梯度下降的方法是通过不断迭代的方式来缩小这个差距，直到该差距收敛到极小值，从而确定参数。
以电子商务推荐算法为例，从建模的角度描述如何通过梯度下降来做参数调优：
用户对于商品的兴趣可以通过简单的线性回归建模，并设计函数h(x)来代表模型预测用户对于某个商品的购买兴趣，如果购买兴趣高，则可以作为商品推荐。模型的公式如下：

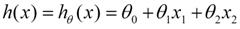
其中X（x1,x2…)是购买行为的特征，例如用户的年龄和喜好，商品类别和价格，参数组θ（θ0，θ1…)表示特征对于预测值的影响大小。
机器学习中除了包括数据分析、特征选择、模型选择之外，还有一个步骤是参数调优。假设 模型的X已经确定，目前需要确定参数组θ，来评估对于特定用户对于特定商品的购买兴趣而言，究竟是商品的价格重要还是用户的爱好影响更重要。
我们需要构建一个损失函数去评估所选择参数的优劣，简单的认为在当前参数组θ，直接比较预测值和真实值差距即可，公式表达为：

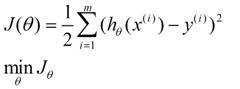
梯度学习方法就是通过调整参数组θ从而让J(θ)取得最小值，调整的方法与从山上顺着梯度朝下一样：

1. 首先对θ初始赋值，这个值可以是随机的，也可以让θ是一个全零的向量。
2. 改变θ的值，使得J(θ)按梯度下降的方向进行减少，直到损失函数差减小收敛到极小值或者0为止。

第二个步骤是关键步骤，就是如何让θi会向着梯度下降的方向进行减少，对于(θ)求偏导J，我们可以进一步得到θ的变化函数：

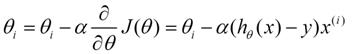
其中α表示步长，h(x)-y表示上次误差，通过上次误差、步长和变量来反馈更新θi。更新的图示如下，其中的两个黑线都是

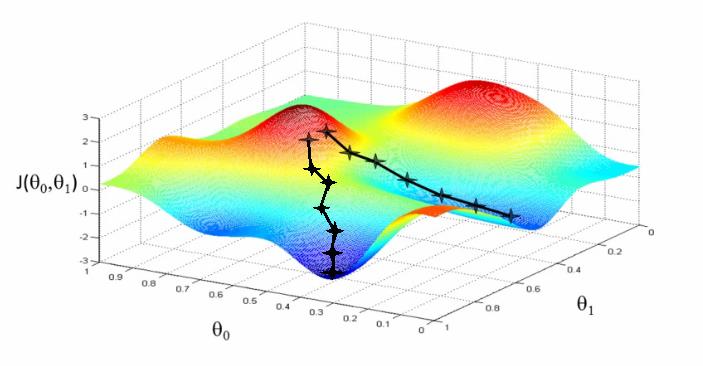
当参数组θ的每一个参数都按照这样的计算公式进行变化更新的时候，模型的预测值将会以梯度的方向接近真实值，最终得到一个最优值，这个最优值可能是局部最优也可能是全局最优，我们将在后面的章节讨论这个问题。

关联概念

在上一章节，我们举的建模样例中提到了一些概念，系统介绍一下：

• 特征x：建模的输入变量，例如商品推荐中商品的价格、类别等参数。
• 预测值：建模h(x)的输出指标，例如商品推荐中预测用户对于某商品的兴趣程度。
• 损失函数 J(θ)：为了评估模型拟合的好坏，通常用损失函数来度量拟合的程度。损失函数极小化，意味着拟合程度最好，对应的模型参数即为最优参数。在线性回归中，损失函数通常为样本输出和假设函数的差取平方。
• 步长：梯度下降过程中，每一步参数变化的长度大小。步长的设置应该仔细斟酌，如果太小，得到最优参数组合的速度很慢（需要迭代的轮数次数会很多），如果太大，收敛过早得到的并非是最优参数，模型的可靠性不高。
• 初始赋值：初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值；当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。
• 退出阈值：当梯度下降的下降幅度达到该阈值时，退出梯度下降。该退出阈值应该尽量接近0（如果有充足的资源进行迭代训练的话），我个人认为最低不大于步长的百分之一，即在最大百分之一步长内的变化即认为收敛到无法变化了。

对于步长和退出阈值应该基于训练数据多次遍历后判断得出。

在训练的时候一个技巧：对特征值x进行归一化处理提高迭代的速度。可以参考博文 的方法。

算法版本

批量梯度下降

批量梯度下降法的做法是，当前一步的梯度下降迭代遍历中参数空间θ的保持不变，当前步结束后，使用更新后的参数θ获得步长大小，然后进行下一步的梯度下降，这就是批量的梯度下降思路。
批量梯度下降的方法需要计算整个数据集才会更新一次参数θ，对于数据集较大的情况下，会非常耗时，另外也不适用于在线更新模型的应用情况，因此应用不太广泛。
代码示例如下:

x = [(1,0.,3) , (1,1.,3) ,(1,2.,3), (1,3.,2) , (1,4.,4)]
y = [95.364,97.217205,75.195834,60.105519,49.342380]
my_break=0.00001
alpha=0.01
diff=0
error1,error0=0,0
theta0,theta1,theta2=0,0,0
sum0,sum1,sum2=0,0,0
while True:
    for i in range(len(x)):
        #批量更新参数
        diff=y[i]-(theta0*x[i][0]+theta1*x[i][1]+theta2*x[i][2])
        sum0=sum0+alpha*diff*x[i][0]
        sum1=sum1+alpha*diff*x[i][1]
        sum2=sum2+alpha*diff*x[i][2]
        count+=1
    theta0,theta1,theta2=sum0,sum1,sum2
    error1=0
    for i in range(len(x)):
        error1+=(y[i]-(theta0*x[i][0]+theta1*x[i][1]+theta2*x[i][2]))**2/2
        count+=1
    if abs(error1-error0)<my_break:
        break
    else:
        error0=error1
print("Done: theta0:{0}, theta1:{1}, theta2:{2}.".format(theta0,theta1,theta2))

随机梯度下降

随机梯度下降与批量梯度下降类似，唯一的区别在于在每一步梯度下降的迭代遍历中，参数空间θ都在变化。也即是说批量梯度下降用所有数据来做梯度下降，随机梯度下降用的是单条数据来做梯度下降。
随机梯度下降的优点是训练速度快，随之而来的是所得到的解并不是最优解，准确度没有批量梯度下降好，尤其是当训练数据噪音比较大的情况。
代码演示如下：

x = [(1,0.,3) , (1,1.,3) ,(1,2.,3), (1,3.,2) , (1,4.,4)]
y = [95.364,97.217205,75.195834,60.105519,49.342380]
my_break=0.00001
alpha=0.01
diff=0
error1,error0=0,0
theta0,theta1,theta2=0,0,0
sum0,sum1,sum2=0,0,0
min_x=2
while True:
    for i in range(len(x)):
        #迭代内参数被单次样本迭代进行更新
        diff=y[i]-(theta0*x[i][0]+theta1*x[i][1]+theta2*x[i][2])
        theta0=theta0+alpha*diff*x[i][0]
        theta1=theta1+alpha*diff*x[i][1]
        theta2=theta2+alpha*diff*x[i][2]
        count+=1
    error1=0
    for i in range(len(x)):
        error1+=(y[i]-(theta0*x[i][0]+theta1*x[i][1]+theta2*x[i][2]))**2/2
        count+=1
    if abs(error1-error0)<my_break:
        break
    else:
        error0=error1
print("Done: theta0:{0}, theta1:{1}, theta2:{2}.".format(theta0,theta1,theta2))

小批量梯度下降

小批量梯度下降结合了批量梯度下降准确度高和随机梯度下降训练速度快的特点，对于训练集m的迭代中，选择x(1<x<m)次迭代后，参数空间θ进行更新。

x = [(1,0.,3) , (1,1.,3) ,(1,2.,3), (1,3.,2) , (1,4.,4)]
y = [95.364,97.217205,75.195834,60.105519,49.342380]
my_break=0.00001
alpha=0.01
diff=0
error1,error0=0,0
theta0,theta1,theta2=0,0,0
sum0,sum1,sum2=0,0,0
count=0
min_x=2
while True:
    count_x=0
    for i in range(len(x)):
        diff=y[i]-(theta0*x[i][0]+theta1*x[i][1]+theta2*x[i][2])
        sum0=sum0+alpha*diff*x[i][0]
        sum1=sum1+alpha*diff*x[i][1]
        sum2=sum2+alpha*diff*x[i][2]
        count_x+=1
        #在迭代内部小批量迭代更新参数
        if count_x%min_x==0:
            theta0,theta1,theta2=sum0,sum1,sum2
        count+=1

    error1=0
    for i in range(len(x)):
        error1+=(y[i]-(theta0*x[i][0]+theta1*x[i][1]+theta2*x[i][2]))**2/2
        count+=1
    if abs(error1-error0)<my_break:
        break
    else:
        error0=error1
print("Done: theta0:{0}, theta1:{1}, theta2:{2}.".format(theta0,theta1,theta2))

过度拟合

梯度下降的目标是在降低预测值和真实值之间的差距从而获得最优的参数空间，基于已有的数据进行迭代训练，需要特别注意”过度拟合“的现象。
防止过度拟合的方法可以参考这篇博文机器学习：防止过拟合的方法 。
这里参考wiki使用Early Stopping的方法来做防止过拟合:

1. 将训练数据分隔成训练集和测试集，80%：20%或者2:1的比例都行；
2. 只基于训练集进行训练，每轮训练集迭代后记录并记为一次EPOCH，每隔N（N=5,8…)个epoch在测试集上运行validation metric进行计算得到validation accuracy并，validation metric可以是模型表现的评估函数；
3. 当连续M（M=10)次EPOCH没有达到最佳的validation accuracy，停止在训练集上的迭代；
4. 记录最佳validation accuracy所对应的参数。

上述的方法是与梯度下降结合使用的，也可以认为在梯度下降的退出条件中增加了一个过渡拟合。除此之外，还可以选择交叉验证、拓展数据集数据等方法来进行过拟合。

局部最优VS全局最优

在不考虑模型过拟合的情况下，梯度下降得到的最优解不一定是全局最优解，也有可能是局部最优解，注意本文第三章节的代码示例中，梯度下降的退出条件：

if abs(error1-error0)<my_break:
    break

在下降过程中，我们找到了一个数据无变化的点（不动点），这个不动点可能有三个含义：极大值、极小值和鞍点。在梯度下降中，极大值基本上可能性没有，只有可能是极小值和鞍点。当前仅当梯度下降是凸函数时，梯度下降会收敛到最小值。
也就是在使用梯度下降中，我们最大可能得到是局部最优解。
为了确保不动点是局部最优解，可以设置更小的退出阈值，进行多次比较看看参数是否变化，如果变化了，说明可以再次调试。
总的来说，梯度下降时一种获得最优解的参数组合的思路，实际应用过程中会结合多种优化方法一起使用。

<wiz_tmp_tag id="wiz-table-range-border" contenteditable="false" style="display: none;">