3.1.1蛮力法之选择排序

Posted 2020-10-10 realswx

        选择排序开始的时候，我们扫描整个列表，找到它的最小元素，然后和第一个元素交换，将最小元素放到它在有序表中的最终位置上。然后我们从第二个元素开始扫描列表，找到最后n-1个元素中的最小元素，再和第二个元素交换位置，把第二小的元素放在它的最终位置上。一般来说，在对该列表做第i遍扫描的时候（i的值从0到n-2），该算法在最后n-i个元素中寻找最小元素，然后拿它和A_i交换。在n-1遍以后，该列表就被排好序了。

算法伪代码（假设列表由数组实现）

SelectionSort(A[0...n-1])

//输入：一个可排序数组A[0...n-1]

//输出：升序排列的数组A[0...n-1]

for i←0 to n-2 do
    min←i
    for j←i+1 to n-1 do
        if A[j]<A[min]    min←j
    swap A[i] and A[min]

执行次数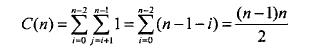

      对于任何输入来说，选择排序都是一个Θ(n²)的算法。然而，请注意，键的交换次数仅为Θ(n)，或者更精确一点，是n-1次（i循环每重复一次执行一次交换）。这个特性使得选择排序优于其他的排序算法。

 

C++代码

#include<iostream>
using namespace std;

void SelectionSort(int a[], int n) {
    for (int i = 0; i < n-1; i++) {
        int min = i;
        for (int j = i + 1; j < n; j++) {
            if (a[j] < a[min])
                min = j;
        }
        swap(a[i], a[min]);
    }
}
int main()
{
    int a[] = {89, 45, 68, 90, 29, 34, 17};
    SelectionSort(a, sizeof(a) / sizeof(a[0]));
    for (int i = 0; i < sizeof(a) / sizeof(a[0]); i++) {
        cout << a[i] << " ";
    }
    cout << endl;
    return 0;
}