结对项目-数独程序扩展 (修改中)
Posted 作业 || 备忘录
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了结对项目-数独程序扩展 (修改中)相关的知识,希望对你有一定的参考价值。
1.项目的Github地址
https://github.com/crvz6182/sudoku_partner
2.开发预估耗时:
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | 10 | |
| · Estimate | · 估计这个任务需要多少时间 | 10 | |
| Development | 开发 | 1270 | |
| · Analysis | · 需求分析 (包括学习新技术) | 30 | |
| · Design Spec | · 生成设计文档 | 10 | |
| · Design Review | · 设计复审 (和同事审核设计文档) | 30 | |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | |
| · Design | · 具体设计 | 30 | |
| · Coding | · 具体编码 | 300 | |
| · Code Review | · 代码复审 | 60 | |
| · Test | · 测试(自我测试,修改代码,提交修改) | 500 | |
| Reporting | 报告 | 120 | |
| · Test Report | · 测试报告 | 85 | |
| · Size Measurement | · 计算工作量 | 5 | |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | |
| 合计 | 1400 |
3.接口设计方法:
设计时主要重视接口是否分工明确,功能是否单一,没有重复。
分工明确:单独设计了用来挖空的接口blank。DLX求解中有很多重复执行的部分,因此拆分成了多个接口(resume,remove,toMartix,dance,delete,init)
功能单一,没有重复:挖空的时候要确定是否有唯一解,没有通过规定参数使求解接口同时实现这个功能,使用专门的接口isunique来判断。
4.计算模块接口的设计与实现过程:
我负责的部分是求解数独,对生成的数独挖空得到题目,命令行部分(参数分析等)和异常处理。
涉及到Core模块中的以下函数:
_declspec(dllexport) bool __stdcall solve(int puzzle[81], int solution[81]);
_declspec(dllexport) bool __stdcall blank(int puzzle[81], int mode);
_declspec(dllexport) bool __stdcall blank(int puzzle[81], int lower, int upper, bool unique);
Node* toMatrix(int puzzle[81]);
void remove(Node* c);
void resume(Node* c);
int dance(Node* head, int solution[81]);
int dance(Node* head, int &tag);
bool DLX(int puzzle[81], int solution[81]);
bool isunique(int puzzle[81]);
void Delete(Node* n);
void init(Node* n);
blank用于对生成好的数独挖空得到题目,挖空时根据传入的参数在范围内随机挖空,会调用isunique判断挖完的题目是否有唯一解,传入参数不合法的话会抛出异常并返回false
由于在实际上玩数独的时候比起解的个数,挖空数对难度的影响要大得多,因此本项目难度的划分不考虑解的个数,具体为:
| 难度 | 挖空个数 |
| 1 | 20~35 |
| 2 | 36~45 |
| 3 | 46~55 |
求解使用了DLX算法,使用链表实现
DLX用于求解数独,会调用dance(Node* head, int solution[81])和toMatrix,返回值表示是否有解
isunique用于判断一个数独题目是否有唯一解,会对数独进行回溯求解,直到回溯完成或找到两个解。是对DLX进行少量重写得到的,返回值表示是否有唯一解
isunique中调用dance(Node* head, int &tag),用tag标记解的个数,tag=2表示有两个以上的解,=1表示唯一解,=0表示无解
init用于初始化链表的节点,Delete用于释放链表的空间
设计函数时将DLX算法分为2个部分:生成链表和遍历。其中遍历会多次执行删除元素和恢复元素的操作。因此将DLX的整个过程分为4个函数
toMatrix用于生成链表,返回head节点
dance(Node* head, int solution[81])用于得出一个解并保存到solution数组里
resume和remove分别用于恢复和删除链表中元素
生成部分:
涉及到的函数有
generate(int number, int result[][81])
void produce(int total, int nums[], int block_num, int & count_total, int count_nums, int sudo[9][9], int result[][81]);
bool isinraw(int num, int raw_num, int sudo[9][9]);
bool isincolumn(int num, int c_num, int sudo[9][9]);
int insert(int num, int blocknum, int marked[], int sudo[9][9]);
void out(int sudo[9][9], int result[][81], int count_total);
生成函数采用的是回溯的方法,该方法虽然不能确保生成的所有数独都不是等价的,但是是尽可能少的产生等价的数独。
5.UML图:
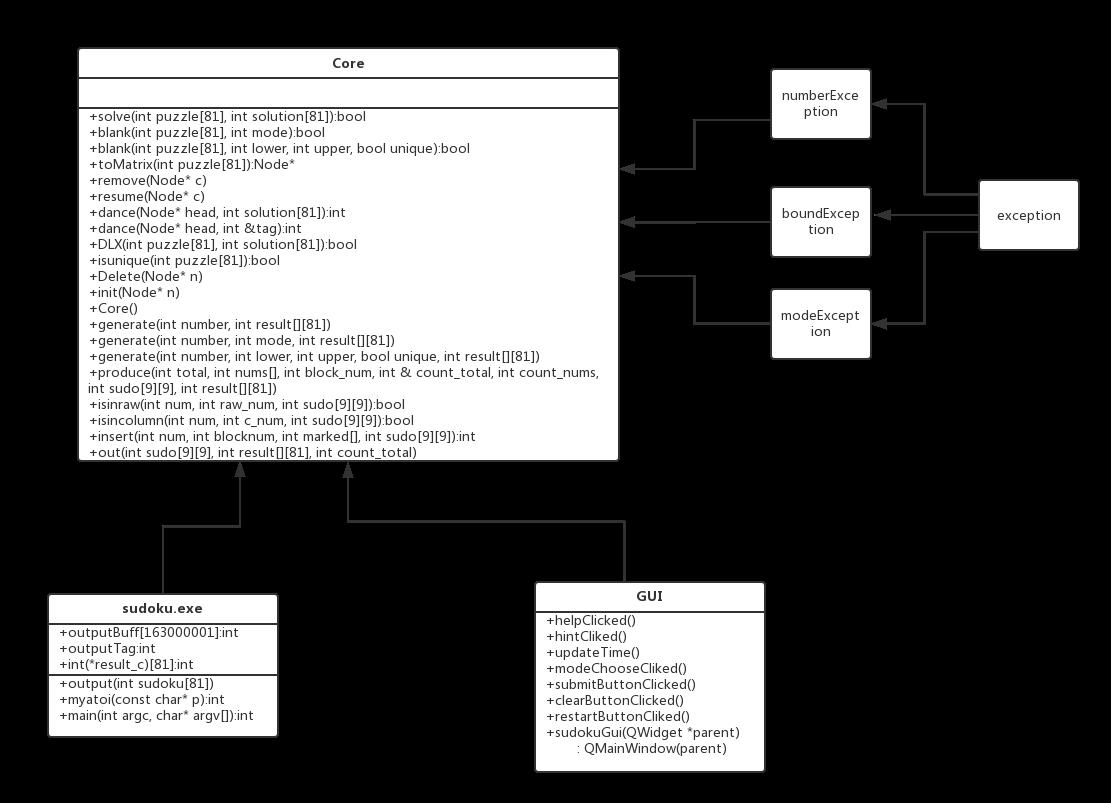
6.计算模块接口部分的性能改进:
基本只对求解进行了改进,但是花费了大量时间(7-8h)
第一版完成时在x86下进行了简单的测试,当时还没有发现问题
在第一版完成以后我们组进行了第四阶段的交换测试,发现在x64环境下DLX求解变得十分慢而且内存消耗极大,在长时间调试后找到了原因
一开始通过中断调试找到了死循环,发现多次挖空时没有还原挖过的数独,修正了挖空的逻辑,但是问题没有得到解决
然后通过内存分析发现链表的Node节点占用了大量的内存,可能是释放链表空间出了问题
经过长时间的分析后发现在求解完成时链表是不完整的,一部分节点被删除,但是变成了孤立节点,没有被释放(仔细想想求解完了的时候链表已经几乎被删空了……)
主要问题出现在dance函数上:
int Core::dance(Node* head, int solution[81]) { if (head->right == head) { return 1; //得到一个解,返回 } Node *i = head->right->right; Node *temp = head->right; while (i != head) { if (i->count<temp->count) temp = i; i = i->right; } if (temp->down == temp)return 0; remove(temp); i = temp->down; while (i != temp) { Node *j = i->right; solution[i->num[0] * 9 + i->num[1]] = i->num[2]; while (j != i) { remove(j->col); j = j->right; } if (dance(head, solution)) { return 1; //依次返回1直到退出递归 } j = i->left; while (j != i) { resume(j->col); j = j->left; } solution[i->num[0] * 9 + i->num[1]] = 0; i = i->down; } resume(temp); //用于恢复链表,但是退出递归的时候不会执行 return 0; }
dance函数递归执行,在一开始链表是完整的,在递归过程中会逐渐删除链表中的元素
当执行到
if (head->right == head) { return 1; }
这段语句的时候,递归的dance函数会逐层返回1并退出。但是这时,链表里面只剩一个head了。以原本的链表索引为基础释放只能释放head,其他元素已经变成了孤立节点。
可以通过在退出递归前还原链表或者建立额外的索引解决
最后经过测试选择了效率较高的方法,在链表中加入了一个额外的指针,使整个链表形成一个一维链表,以此为索引进行释放就不会漏掉节点,最终解决了问题
性能分析
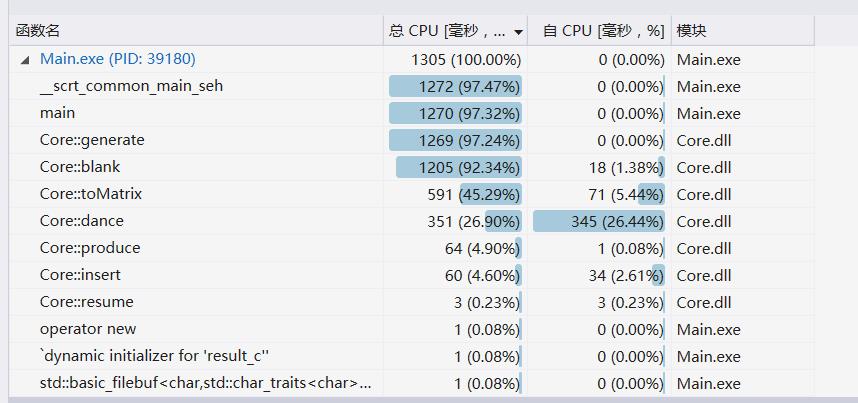
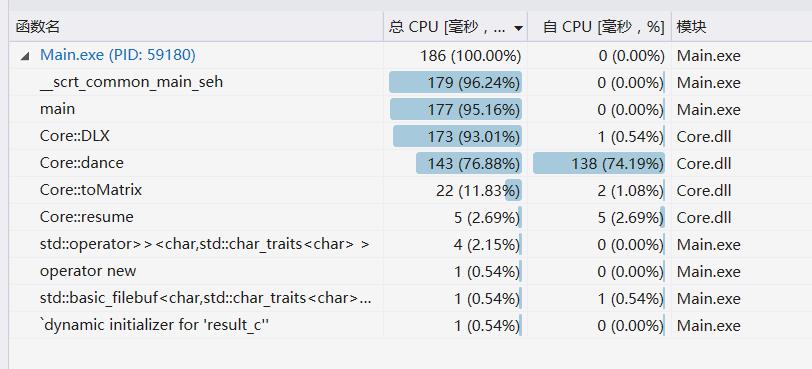
两张分别对应生成数独题和求解,生成参数为 -n 100 -u,求解为多次求解一个较难的17个数的数独
由于generate调用了blank,blank调用了isunique,isunique调用了toMatrix和dance,时间主要消耗在转换成矩阵上,求解也花了一定量的时间。
求解的时候选用了难度较大的数独,这时dance函数消耗的时间明显上升
在使用-u参数的时候,由于需要多次求解和重新挖空,效率很慢,生成100个就要5s,目前还没有找到什么比较好的解决办法
7.Design by Contract, Code Contract:
契约式编程保证了调用者和被调用和双方的质量,避免调用方的代码质量明显较差,但缺点是需要一种机制,对程序设计语言有要求
在结对编程中,两方的地位平等,分工明确,这对于使用契约式编程来说是个很好的环境。
在项目中我主要负责编写被调用者(Core),另一位同学负责调用者(GUI)
双方分别明确接口规格,对自己的部分负责,并进行完善的测试,这可以有效避免组合在一起时出现bug,节省时间。
8.计算模块部分单元测试展示:
测试生成:
TEST_METHOD(TestGenerate)
{
// TODO: 在此输入测试代码
int sudo[9][9];
Core test;
int result[3][81];
test.generate(3, result);
for (int i = 0; i < 3; i++)
{
for (int j = 0; j < 81; j++)
{
sudo[j / 9][j % 9] = result[i][j];
}
for (int j = 0; j < 9; j++)
{
for (int k = 0; k < 9; k++)
{
for (int n = 0; n < 9; n++)
{
if (n != j)
{
Assert::AreEqual(false, sudo[i][j] == sudo[i][n]);
}
if (n != i)
{
Assert::AreEqual(false, sudo[i][j] == sudo[n][j]);
}
}
}
}
}
int blankNum = 0;
int puzzle[81] = { 8,1,2,7,5,3,6,4,9,9,4,3,6,8
,2,1,7,5,6,7,5,4,9,1,2,8,3,1,5,4,2,3,7,8,9
,6,3,6,9,8,4,5,7,2,1,2,8,7,1,6,9,5,3,4,5,2
,1,9,7,4,3,6,8,4,3,8,5,2,6,9,1,7,7,9,6,3,1
,8,4,5,2 };
int backup[81] = { 8,1,2,7,5,3,6,4,9,9,4,3,6,8
,2,1,7,5,6,7,5,4,9,1,2,8,3,1,5,4,2,3,7,8,9
,6,3,6,9,8,4,5,7,2,1,2,8,7,1,6,9,5,3,4,5,2
,1,9,7,4,3,6,8,4,3,8,5,2,6,9,1,7,7,9,6,3,1
,8,4,5,2 };
test.generate(1, 1, result);
for (int i = 0; i < 81; i++)
{
if (result[0][i] == 0)
{
blankNum++;
result[0][i] = backup[i];
}
}
Assert::AreEqual((20 <= blankNum&&blankNum <= 35), true);
blankNum = 0;
test.generate(1, 2, result);
for (int i = 0; i < 81; i++)
{
if (result[0][i] == 0)
{
blankNum++;
result[0][i] = backup[i];
}
}
Assert::AreEqual((36 <= blankNum&&blankNum <= 45), true);
blankNum = 0;
test.generate(1, 3, result);
for (int i = 0; i < 81; i++)
{
if (result[0][i] == 0)
{
blankNum++;
result[0][i] = backup[i];
}
}
Assert::AreEqual((46 <= blankNum&&blankNum <= 55), true);
blankNum = 0;
test.generate(1, 20, 55, true, result);
for (int i = 0; i < 81; i++)
{
if (result[0][i] == 0)
{
blankNum++;
result[0][i] = backup[i];
}
}
Assert::AreEqual((20 <= blankNum&&blankNum <= 55), true);
blankNum = 0;
test.generate(1, 40, 40, true, result);
for (int i = 0; i < 81; i++)
{
if (result[0][i] == 0)
{
blankNum++;
result[0][i] = backup[i];
}
}
Assert::AreEqual((40 == blankNum), true);
}
分别针对生成的三种接口进行测试,检测生成的数独终局是否合法/题目是否符合要求
测试求解:
TEST_METHOD(TestSolve) { // TODO: 在此输入测试代码 int puzzle[81] = { 8,0,0,0,0,0,0,0,0 ,0,0,3,6,0,0,0,0,0 ,0,7,0,0,9,0,2,0,0 ,0,5,0,0,0,7,0,0,0 ,0,0,0,0,4,5,7,0,0 ,0,0,0,1,0,0,0,3,0 ,0,0,1,0,0,0,0,6,8 ,0,0,8,5,0,0,0,1,0 ,0,9,0,0,0,0,4,0,0,}; int result[81] = { 0 }; int answer[81] = { 8,1,2,7,5,3,6,4,9,9,4,3,6,8 ,2,1,7,5,6,7,5,4,9,1,2,8,3,1,5,4,2,3,7,8,9 ,6,3,6,9,8,4,5,7,2,1,2,8,7,1,6,9,5,3,4,5,2 ,1,9,7,4,3,6,8,4,3,8,5,2,6,9,1,7,7,9,6,3,1 ,8,4,5,2 }; int wrong[81] = { 8,1,2,7,5,3,6,4,9,9,4,3,6,8 ,2,1,7,5,6,7,5,4,9,1,8,2,3,1,5,4,2,3,7,8,9 ,6,3,6,9,8,4,5,7,2,1,2,8,7,1,6,9,5,3,4,5,2 ,1,9,7,4,3,6,8,4,3,8,5,2,6,9,1,7,7,9,6,3,1 ,8,4,5,2 }; Core test; bool isvalid = true; test.solve(puzzle, result); for (int i = 0; i < 81; i++) {
puzzle[i] = answer[i]; Assert::AreEqual(result[i], answer[i]); } test.blank(puzzle, 20, 55, true); test.solve(puzzle, result); for (int i = 0; i < 81; i++) { Assert::AreEqual(result[i], answer[i]); } isvalid = test.solve(wrong, result); Assert::AreEqual(isvalid, false); isvalid = test.solve(answer, result); Assert::AreEqual(isvalid, true); }
依次求解一个较难的数独,随机挖空的唯一解数独,不合法的数独和完整的合法数独,检测求解的结果和返回值正不正确
同时检测了判断唯一解算法的正确性,若返回的数独不是唯一解的话求解出的result和answer可能不相同,不能通过测试
单元测试覆盖率:

9.计算模块部分异常处理说明:
项目的异常分为三种:
| numberException | 输入的数独生成数量异常 |
| boundException | 输入的挖空边界异常 |
| modeException | 输入的难度异常 |
TEST_METHOD(TestException) { Core test; int result[3][81]; try { test.generate(2000000, result); } catch (numberException &e) { Assert::AreEqual(0, 0); } try { test.generate(20000, 2, result); } catch (numberException &e) { Assert::AreEqual(0, 0); } try { test.generate(20000, 20, 40, false, result); } catch (numberException &e) { Assert::AreEqual(0, 0); } try { test.generate(3, 5, result); } catch (modeException &e) { Assert::AreEqual(0, 0); } try { test.generate(3, 41, 40, false, result); } catch (boundException &e) { Assert::AreEqual(0, 0); } try { test.generate(3, 12, 40, false, result); } catch (boundException &e) { Assert::AreEqual(0, 0); } try { test.generate(3, 32, 70, false, result); } catch (boundException &e) { Assert::AreEqual(0, 0); } }
单元测试分别针对使用-c和-n时的参数,难度不为1-3,边界超出范围和lower>upper等情况进行了测试
test.generate(2000000, result);
|
使用参数-c,超出了最大范围1000000 |
test.generate(20000, 2, result)
|
使用参数-n,超出了最大范围10000 |
test.generate(20000, 20, 40, false, result)
|
使用参数-n,超出了最大范围10000 |
test.generate(3, 5, result)
|
使用参数-m,输入的参数不在1~3范围内 |
test.generate(3, 41, 40, false, result)
|
使用参数-r,lower>upper |
test.generate(3, 12, 40, false, result)
|
使用参数-r,lower超出范围 |
test.generate(3, 32, 70, false, result)
|
使用参数-r,upper超出范围 |
10.界面模块的详细设计过程:
界面主要分为两部分:菜单栏和主界面。菜单栏实现的功能有难度的选择,help文档,主界面实现的功能有重新开始、清空、提示、提交、计时以及最佳记录。
**数独盘**:通过81个单行文本框实现,继承了QLineEdit类实现MyLineEdit类,重写了contextMenuEvent方法,新增了hint信号以及槽函数为了实现提示功能,新增setRead方法,使得题目中的数字背景变色以及hint失效。
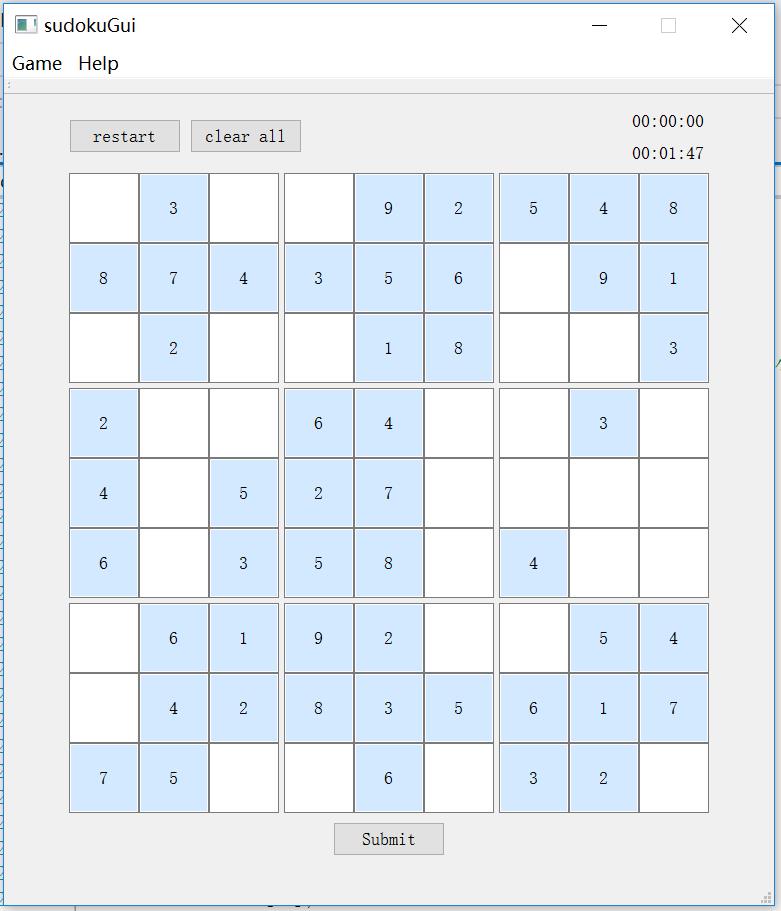
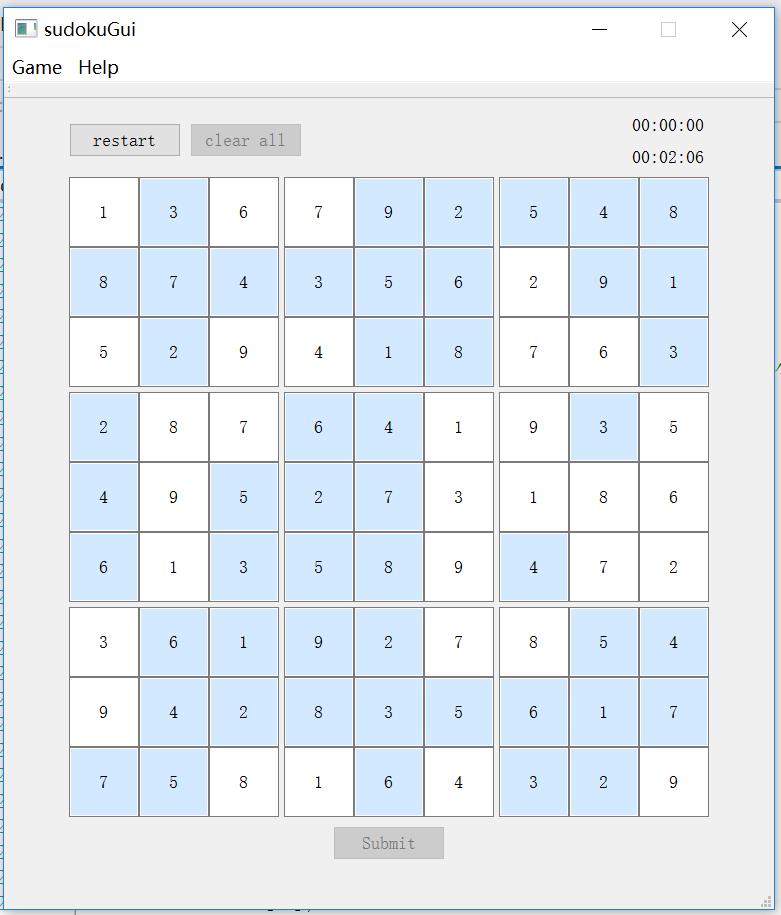
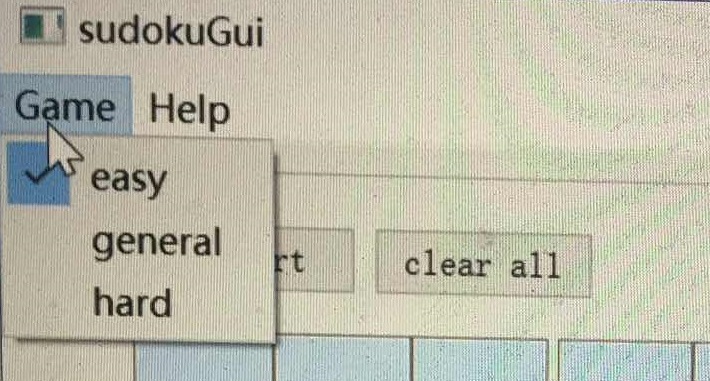
**模式选择**:在菜单中实现,通过点击执行相对应的槽函数,实现难度的改变。
**提示**:通过点击相应空格的右键进行提示,该动作的槽函数在自己写的MyLineEdit类里,该函数是发送信号,在主界面接受到信号后调用相应的函数求解并提示。

**计时以及最佳记录**:通过实现定时器和QTimer实现,让定时器每隔一秒触发一次,更新时间并输入到文本框当中。最佳纪录是在提交成功解正确后比对当前时间与最佳纪录,若当前时间短则更新,通过一个字符串保存在类里。
具体布局代码如下:
``` //布局 QGridLayout *layout = new QGridLayout; layout->addWidget(restartButton, 0, 0, 2, 1, 0); // 重新开始按钮 layout->addWidget(clearButton, 0, 1, 2, 1, 0); // 清空按钮 layout->addWidget(bestRecord, 0, 8, 1, 1, Qt::AlignRight); //最佳纪录时间 layout->addWidget(nowRecord, 1, 8, 1, 1, Qt::AlignRight); //已经用时 layout->addLayout(layoutSudo, 2, 0, 1, 9, Qt::AlignCenter); // 9*9的方正 layout->addWidget(submitButton, 3, 0, 1, 9, Qt::AlignCenter); // 提交按钮 ```
计时部分代码如下:
设置1秒触发一次,调用updateTime函数,加一秒并更新文本框。
``` QLineEdit *bestRecord; // 显示最好记录的时间 QLineEdit *nowRecord; // 显示现在的时间 QString record; connect(timer, SIGNAL(timeout()), this, SLOT(updateTime())); timer->start(1000); void QtGuiApplication2::updateTime() { *TimeRecord = TimeRecord->addSecs(1); nowRecord->setText(TimeRecord->toString("hh:mm:ss")); } ```
提示部分代码如下:
点击hint后,发出信号,在主界面接收到信号调用hintClicked()函数。
``` class MyLineEdit :public QLineEdit { protected: QMenu * hintMenu = new QMenu(); QAction * action = hintMenu->addAction("hint"); void contextMenuEvent(QContextMenuEvent *event); signals: void hint(); public slots : void hintCliked(); } connect(blocks[nowNum], SIGNAL(hint()), this, SLOT(hintCliked())); // 提示绑定事件
11.界面模块与计算模块的对接:
- 要使用计算模块的功能首先要配置相应的dll,我们参考了这篇[博客](http://www.cnblogs.com/houkai/archive/2013/06/05/3119513.html)。
- 接下来是具体的调用部分
- 首先创建了一个core对象,供调用函数。
- 初始化的时候调用generate(1, mode, sudo),生成一个简单的数独局。
- 重新开始按钮点击后,需要生成新的数独局,同样调用generate函数。
- 在提交按钮点击后,需要先判断填写是否正确,错误的话应该显示正确答案,此时先调用solve函数判断解的正确性,若错误,再次调用solve函数。
- 模式选择中,每次选择一个模式,都需要生成相应模式的数独,调用generate函数并传入相应的模式难度参数。
- 提示被点击之后,要在该空显示出数字,调用solve并取出对应位置的数填写即可。
- 实现的功能有:模式选择,帮助菜单,重新开始,清空当前所有,计时功能,最佳纪录,提示功能
12.描述结对的过程:
主要的讨论都在网上进行,在确定结对后线上讨论得出分工,之后制订计划并开始编码
讨论的结果是我负责除GUI和生成完整数独算法以外的任务
在下课的时候会当面讨论一些线上无法解决的问题

13.优点和缺点:
结对编程的优点:在开发一个不需要大量研究的项目时,可以有效提高工作效率和编码质量,减少不经意间产生的bug,两个人也可以互相学习
缺点:分工和规则的制定有些麻烦,需要两个人的配合和互相理解
她的优点:
写的代码在交给我的时候几乎没有bug,我没有做到这一点
擅长交流,我们可以很有效地沟通
可以即时接受反馈并改进
缺点:
没有主动报告自己的进度
14.开发实际耗时:
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
| Planning | 计划 | 10 | 10 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | 1270 | 1160 |
| · Analysis | · 需求分析 (包括学习新技术) | 20 | 60 |
| · Design Spec | · 生成设计文档 | 10 | 20 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 30 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 60 | 60 |
| · Coding | · 具体编码 | 300 | 300 |
| · Code Review | · 代码复审 | 60 | 60 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 500 | 450 |