[杂谈] 编程为什么要学算法 - 某程序媛计划有感

Posted 2020-10-10

最近那谁出的程序媛计划，先不说这个事情是好是坏，这个程序做的是好是坏（坏）...

只是最近微博上，尤其是非CST专业的人，居然有很多人认为入门学编程不需要学习算法....

连程序媛计划的发起人都在微博中说 “不需要数学和英文基础”

而其支持者的态度也是 “入门时不需要学习算法，甚至工作中用到算法的也不多，用到了再学就行”

 

不得不说这真是一副培训班的忽悠口吻....

 

入门为什么要学算法？

并不是说不学算法就没法学编程，而是说接触了算法之后，会帮助更好的去思考编程的逻辑，而这个逻辑的培养正是新手学习编程的初期最需要的东西。

（至于工作后不需要算法这个事情就懒得吐槽了，大概是我们对程序员有不同的理解吧）

---

 

 

举个栗子：

计算一个数的平方根，编写一个函数，input一个数字，output这个数字的平方根的近似值

 

1. 用最接近人类的方法实现：

如果是没有数学基础的人，其想法一般是什么呢？

先取一个小的数字 a，计算 a的平方，如果a的平方小于input数字，则把a加大，
然后循环，直到大于或等于input数字了，则这时的a就是input数字的平方根的近似值

不仅没有考虑精度问题，函数不仅完全没有效率，也会出现很多错误

x = 25
epsilon = 0.01
step = epsilon**2
numGuesses = 0
ans = 0.0
while (abs(ans**2 - x)) >= epsilon and ans <= x:
    ans += step
    numGuesses += 1
print(‘numGuesses = ‘ + str(numGuesses))
if abs(ans**2-x) >= epsilon:
    print(‘Failed on square root of ‘ + str(x))
else:
    print(str(ans) + ‘ is close to the square root of ‘ + str(x))

在这个方法中，仅仅是求x=25的近似平方根，就会执行49990次，而且精度很低

numGuesses = 49990
4.999 is close to the square root of 25

 

2. 用稍微clever的方法实现

如果现在你已经有一些“聪明”的想法，或者知道有个算法叫二分法，那么便可以写出聪明的方法

注意，现在你已经不是 “完全不需要算法的状态了”

二分法简单的图示

 

 

# 二分法计算平方根
x = 12345
epsilon = 0.01
numGuesses = 0
low = 0.0
high = x
ans = (high + low)/2.0
while abs(ans**2 - x) >= epsilon:
    numGuesses += 1
    if ans**2 < x:
        low = ans
    else:
        high = ans
    ans = (high + low)/2.0
print(‘numGuesses = ‘ + str(numGuesses))
print(str(ans) + ‘ is close to square root of ‘ + str(x))

同样计算25的平方根，只需要计算13次，而且精度更高

numGuesses = 13
5.00030517578 is close to square root of 25

计算12345五位数的平方根，也没有增加多少，只需要26次

numGuesses = 26
111.108076461 is close to square root of 12345

 

3. 用数学的方法实现

这个时候就开始需要数学了，从这里开始，也变得越来越复杂，效率也变得越来越高

3.1 牛顿-拉夫逊 （Newton & Raphson) 算法

最基础的平方根算法之一

其数学原理为：

用公式表示为：

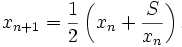
# Newton-Raphson for square root
epsilon = 0.01
y = 12345.0
guess = y/2.0
numGuesses = 0
while abs(guess*guess - y) >= epsilon:
    numGuesses += 1
    guess -= ((guess**2) - y)/(2*guess)
    # print(guess)
print(‘numGuesses = ‘ + str(numGuesses))
print(‘Square root of ‘ + str(y) + ‘ is about ‘ + str(guess))

此时，计算12345五位数的平方根，仅需要9次

numGuesses = 9
Square root of 12345.0 is about 111.108057705

 

---

你以为这就结束了？

远远不呢，3.1的方法中，有一个明显的缺陷就是初始值的选择，虽然使用了牛顿法去收敛，但初始值仍然是 y/2.0

那么，如果我们能够一开始就选择一个非常近似的值，就能够大大减少计算的次数，提高运算效率了

 

3.2 基于泰勒公式的级数逼近（泰勒级数+牛顿法）

微积分中的泰勒级数可以表示为：

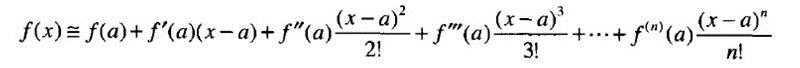
符号a表示某个常量，记号f‘、f‘‘和f‘‘‘表示函数f的一阶、二阶和三阶导数，以此类推

这个公式称为泰勒公式，基于这个公式，我们平方根公式的展开式为：

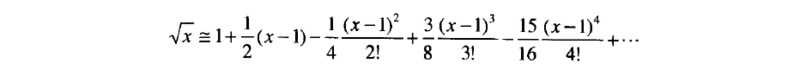
根据该公式我们可以在一定精度内逼近真实值。

在泰勒级数展开中，平方根函数的公式当且仅当参数值位于一个有效范围内时才有效，在该范围内计算趋于收敛。

该范围即是收敛半径，当我们对平方根函数用a=1进行计算时，泰勒级数公式希望x处于范围:$0<x<2$之间。

如果x在收敛半径之外，则展开式中的项会越来越大，泰勒级数离答案也就越来越远。

为了解决该问题，我们可以考虑当待开平方数大于4时以4去除它，最后将得到的数乘以相同次数的2即可。

C参考实现（Github上的方法，原链接似乎失效了）

public double TSqrt() {
    //设置修正系数
    double correction = 1;
    //因为要对原值进行缩小,因此设置临时值
    double tempValue = value;
    while (tempValue >= 2) {
        tempValue = tempValue / 4;
        correction *= 2;
    }
    return this.TSqrtIteration(tempValue) * correction;
}
private double TSqrtIteration(double value) {
    double sum = 0, coffe = 1, factorial = 1, xpower = 1, term = 1;
    int i = 0;
    while (Math.abs(term) > 0.000001) {
        sum += term;
        coffe *= (0.5 - i);
        factorial *= (i + 1);
        xpower *= (value - 1);
        term = coffe * xpower / factorial;
        i++;
    }
    return sum;
}

 

---

再次，你以为这就结束了？

图样图奶衣服

 

3.3 平方根倒数速算法（卡马克快速平方根算法）（What the FUCK方法）

这个方法实在可怕，完全不明白

其通俗的解释为：

首先接收一个32位带符浮点数，然后将之作为一个32位整数看待，以将其向右进行一次逻辑移位的方式将之取半。

用十六进制“魔术数字” 0x5f3759df 减之，如此即可得对输入的浮点数的平方根倒数的首次近似值；

而后重新将其作为浮点数，以牛顿法计算，求出更精确的近似值。

在计算浮点数的平方根倒数的同一精度的近似值时，此算法比直接使用浮点数除法要快四倍。

 

在wiki上帝详细解释，认输.jpg：

https://en.wikipedia.org/wiki/Fast_inverse_square_root

 

float InvSqrt (float x)
{
    float xhalf = 0.5f*x;
    int i = *(int*)&x;
    i = 0x5f3759df - (i >> 1); // 计算第一个近似根
    x = *(float*)&i;
    x = x*(1.5f - xhalf*x*x); // 牛顿迭代法
    return x;
}

对没错只有这么点儿，而且那个 0x5f3759df 是什么玩意儿？

而且它通过某种方法算出了一个与真根非常接近的近似根，因此它只需要使用一次迭代过程就获得了较满意的解。

 

以下引用链接中对此方法的解释：

http://www.cnblogs.com/vagerent/archive/2007/06/25/794695.html

 

IEEE标准下，float类型的数据在32位系统上是这样表示的（大体来说就是这样，但省略了很多细节，有兴趣可以GOOGLE）：

bits：31 30 ... 0
31：符号位
30-23：共8位，保存指数（E）
22-0：共23位，保存尾数（M）

所以，32位的浮点数用十进制实数表示就是：M*2^E。

开根然后倒数就是：M^(-1/2)*2^(-E/2)。

现在就十分清晰了。语句i> >1其工作就是将指数除以2，实现2^(E/2)的部分。

而前面用一个常数减去它，目的就是得到M^(1/2)同时反转所有指数的符号。

 

至于那个0x5f3759df，呃，我只能说，的确是一个超级的Magic Number。

那个Magic Number是可以推导出来的，但我并不打算在这里讨论，因为实在太繁琐了。

简单来说，其原理如下：因为IEEE的浮点数中，尾数M省略了最前面的1，所以实际的尾数是1+M。

如果你在大学上数学课没有打瞌睡的话，那么当你看到(1+M)^(-1/2)这样的形式时，应该会马上联想的到它的泰勒级数展开，而该展开式的第一项就是常数。

下面给出简单的推导过程：

对于实数R>0，假设其在IEEE的浮点表示中，
指数为E，尾数为M，则：

R^(-1/2)
= (1+M)^(-1/2) * 2^(-E/2)

将(1+M)^(-1/2)按泰勒级数展开，取第一项，得：

原式
= (1-M/2) * 2^(-E/2)
= 2^(-E/2) - (M/2) * 2^(-E/2)

如果不考虑指数的符号的话，
(M/2)*2^(E/2)正是(R>>1)，
而在IEEE表示中，指数的符号只需简单地加上一个偏移即可，
而式子的前半部分刚好是个常数，所以原式可以转化为：

原式 = C - (M/2)*2^(E/2) = C - (R>>1)，其中C为常数

所以只需要解方程：
R^(-1/2)
= (1+M)^(-1/2) * 2^(-E/2)
= C - (R>>1)
求出令到相对误差最小的C值就可以了

 

---

最后，引用链接中的code，对3.1-3.3三种算法进行效率对比

https://segmentfault.com/a/1190000006122223

@Test
public void testBabylonian() {
    for (int i = 0; i < 10000; i++) {
        Assert.assertEquals(2.166795861438391, squareRoots.Babylonian(), 0.000001);
    }
}

@Test
public void testTSqrt() {
    for (int i = 0; i < 10000; i++) {
        Assert.assertEquals(2.166795861438391, squareRoots.TSqrt(), 0.000001);

    }
}

@Test
public void testFastInverseSquareRoot() {
    for (int i = 0; i < 10000; i++) {
        Assert.assertEquals(2.1667948388864198, squareRoots.FastInverseSquareRoot(), 0.000001);
    }
}

View Code

@Test
public void benchMark() {

    //巴比伦算法计时器
    long babylonianTimer = 0;

    //级数逼近算法计时器
    long tSqrtTimer = 0;

    //平方根倒数速算法计时器
    long fastInverseSquareRootTimer = 0;

    //随机数生成器
    Random r = new Random();
    for (int i = 0; i < 100000; i++) {
        double value = r.nextDouble() * 1000;
        SquareRoots squareRoots = new SquareRoots(value);
        long start, stop;
        start = System.currentTimeMillis();
        squareRoots.Babylonian();
        babylonianTimer += (System.currentTimeMillis() - start);
        start = System.currentTimeMillis();
        squareRoots.TSqrt();
        tSqrtTimer += (System.currentTimeMillis() - start);
        start = System.currentTimeMillis();
        squareRoots.FastInverseSquareRoot();
        fastInverseSquareRootTimer += (System.currentTimeMillis() - start);
    }

    System.out.println("巴比伦算法:" + babylonianTimer);
    System.out.println("级数逼近算法:" + tSqrtTimer);
    System.out.println("平方根倒数速算法:" + fastInverseSquareRootTimer);

}

View Code

最后的结论是：

结果为:
巴比伦算法:17
级数逼近算法:34
平方根倒数速算法:7

 

---

最最后，附赠一个关于魔法数字 0x5f3759df 的链接（看不懂）

http://blog.jobbole.com/105295/

 

---

 

怎么样？编程很好玩吧？

（不

也许我们工作中大部分的程序员都用不到如此级别的算法，但是说算法完全用不到是不可能的，即使是最最不需要数学的二分法，也是算法了。

而且，在学习编程的时候，研究这些 “聪明” 的方法，或者仅仅是观看，也会享受到编程的乐趣，和逻辑的美。

这对提高兴趣有极大的帮助，总不能一辈子做一个苦逼的初级码农吧。

 

希望本文能够为初学者提供一个正确学习编程的思路：“ 编程为什么需要研究算法？”

 

---

 

对了，如果你问为什么一个计算平方根，要搞得如此变态？反正电脑的计算速度很强不是吗？

其实方法3.3 最早于计算机图形学的硬件与软件领域有所应用，如SGI和3dfx就曾在产品中应用此算法。

在 3D 图形中，你使用平面法线，长度为 1 的三坐标向量，来表示光线和反射。

你会使用很多平面法线，计算它们时需要对向量进行标准化。

而如何标准化一个向量呢？每个坐标分别除以向量的长度，因此，每个坐标需乘上

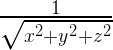
计算平方和加法相对开销很小，但计算平方根和除法，就需要很大的开销了。

 

想想3D图形中，用到这个计算的地方会有多少？当这个开销被放大到非常大时，还使用笨办法，电脑的计算能力还扛得住吗？