软件应用开发技术之四：MD5算法解析及实现

Posted 2020-10-10 木南创智

MD5即Message-Digest Algorithm 5（信息-摘要算法5），用于确保信息传输完整一致。是计算机广泛使用的杂凑算法之一（又译摘要算法、哈希算法），主流编程语言普遍已有MD5实现。

1、MD5算法简介

MD5在90年代初由MIT的计算机科学实验室和RSA Data Security Inc发明，经MD2、MD3和MD4发展而来。

MD5将任意长度的“字节串”变换成一个128bit的大整数，并且它是一个不可逆的字符串变换算法，换句话说就是，即使你看到源程序和算法描述，也无法将一个MD5的值变换回原始的字符串，从数学原理上说，是因为原始的字符串有无穷多个。

MD5的典型应用是对一段信息串 (Message)产生所谓的指纹 (fingerprint)，以防止被“篡改”。比方说，你将一段话写在一个文本文件中，并对这个文本文件产生一个MD5的值并记录在案，然后你可以传播这个文件给别人，别人如果修改了文件中的任何内容，你对这个文件重新计算MD5时就会发现。如果再有一个第三方的认证机构，用MD5还可以防止文件作者的“抵赖”，这就是所谓的数字签名应用。

MD5还广泛用于加密和解密技术上，在很多操作系统中，用户的密码是以MD5值（或类似的其它算法）的方式保存的，用户Login的时候，系统是把用户输入的密码计算成MD5值，然后再去和系统中保存的MD5值进行比较，而系统并不“知道”用户的密码是什么。

2、MD5算法分析

前面我们提到了MD5算法的主要应用领域，那么究竟MD5算法具体是什么样的呢？接下来我们就对其原理进行一些说明。

（1）待加密信息处理

显而易见，我们要对一个字符串进行MD5计算，那么肯定要从这个字符串的处理入手。我们知道一个字符的长度是一个字节，即8位（bit）的长度。MD5对待加密的字符串的处理是将一个字符串分割成每512位为一个分组，形如N*512+R，这里的R是余下的位数。这个R分为几种情况：

R=0时，需要补位，单补上一个512位的分组，因为还要加入最后64个位的字符串长度。

R<448时，则需要补位到448位，后面添加64位的字符串长度。

R>448时，除了补满这一分组外，还要再补上一个512位的分组后面添加64位的字符串长度。

补位的形式是先填充一个1，再接无数个0，直到补足512位。

（2）MD5的链接变量及基本操作

 MD5有四个32位的被称作链接变量的整数参数，这是个参数我们定义为A、B、C、D其取值为：A=0x01234567，B=0x89abcdef，C=0xfedcba98，D=0x76543210。但考虑到内存数据存储大小端的问题我们将其赋值为：A=0x67452301，B=0xefcdab89，C=0x98badcfe，D=0x10325476。

同时MD5算法规定了四个非线性操作函数（&是与，|是或，~是非，^是异或）：

F(X,Y,Z) =(X&Y)|((~X)&Z)

G(X,Y,Z) =(X&Z)|(Y&(~Z))

H(X,Y,Z) =X^Y^Z

I(X,Y,Z)=Y^(X|(~Z))

这些函数是这样设计的：如果X、Y和Z的对应位是独立和均匀的，那么结果的每一位也应是独立和均匀的。

利用上面的四种操作，生成四个重要的计算函数。首先我们声明四个中间变量a,b,c,d，赋值：a = A, b = B, c = C, d = D。然后定义这四个计算函数为：

FF(a, b, c, d, M[j], s, ti)表示 a = b + ((a + F(b, c, d) + Mj + ti) <<< s)

GG(a, b, c, d, M[j], s, ti)表示 a = b + ((a + G(b, c, d) + Mj + ti) <<< s)

HH(a, b, c, d, M[j], s, ti)表示 a = b + ((a + H(b, c, d) + Mj + ti) <<< s)

II(a, b, c, d, M[j], s, ti)表示 a = b + ((a + I(b, c, d) + Mj + ti) <<< s)

其中M[j]表示消息的第j个子分组（从0到15），<<表示循环左移s，常数ti是4294967296*abs(sin(i))的整数部分，i取值从1到64，单位是弧度。

（3）循环计算

定义好上述的四个计算函数后，就可以实现MD5的真正循环计算了。这个循环的循环次数为512位分组的个数。每次循环执行64不计算，上述4个函数每个16次，具体如下：

//第一轮循环计算

        FF(a,b,c,d,M[0],7,0xd76aa478);

        FF(d,a,b,c,M[1],12,0xe8c7b756);

        FF(c,d,a,b,M[2],17,0x242070db);

        FF(b,c,d,a,M[3],22,0xc1bdceee);

        FF(a,b,c,d,M[4],7,0xf57c0faf);

        FF(d,a,b,c,M[5],12,0x4787c62a);

        FF(c,d,a,b,M[6],17,0xa8304613);

        FF(b,c,d,a,M[7],22,0xfd469501) ;

        FF(a,b,c,d,M[8],7,0x698098d8) ;

        FF(d,a,b,c,M[9],12,0x8b44f7af) ;

        FF(c,d,a,b,M[10],17,0xffff5bb1) ;

        FF(b,c,d,a,M[11],22,0x895cd7be) ;

        FF(a,b,c,d,M[12],7,0x6b901122) ;

        FF(d,a,b,c,M[13],12,0xfd987193) ;

        FF(c,d,a,b,M[14],17,0xa679438e) ;

        FF(b,c,d,a,M[15],22,0x49b40821);

 

        //第二轮循环计算

        GG(a,b,c,d,M[1],5,0xf61e2562);

        GG(d,a,b,c,M[6],9,0xc040b340);

        GG(c,d,a,b,M[11],14,0x265e5a51);

        GG(b,c,d,a,M[0],20,0xe9b6c7aa) ;

        GG(a,b,c,d,M[5],5,0xd62f105d) ;

        GG(d,a,b,c,M[10],9,0x02441453) ;

        GG(c,d,a,b,M[15],14,0xd8a1e681);

        GG(b,c,d,a,M[4],20,0xe7d3fbc8) ;

        GG(a,b,c,d,M[9],5,0x21e1cde6) ;

        GG(d,a,b,c,M[14],9,0xc33707d6) ;

        GG(c,d,a,b,M[3],14,0xf4d50d87) ;

        GG(b,c,d,a,M[8],20,0x455a14ed);

        GG(a,b,c,d,M[13],5,0xa9e3e905);

        GG(d,a,b,c,M[2],9,0xfcefa3f8) ;

        GG(c,d,a,b,M[7],14,0x676f02d9) ;

        GG(b,c,d,a,M[12],20,0x8d2a4c8a);

 

        //第三轮循环计算

        HH(a,b,c,d,M[5],4,0xfffa3942);

        HH(d,a,b,c,M[8],11,0x8771f681);

        HH(c,d,a,b,M[11],16,0x6d9d6122);

        HH(b,c,d,a,M[14],23,0xfde5380c) ;

        HH(a,b,c,d,M[1],4,0xa4beea44) ;

        HH(d,a,b,c,M[4],11,0x4bdecfa9) ;

        HH(c,d,a,b,M[7],16,0xf6bb4b60) ;

        HH(b,c,d,a,M[10],23,0xbebfbc70);

        HH(a,b,c,d,M[13],4,0x289b7ec6);

        HH(d,a,b,c,M[0],11,0xeaa127fa);

        HH(c,d,a,b,M[3],16,0xd4ef3085);

        HH(b,c,d,a,M[6],23,0x04881d05);

        HH(a,b,c,d,M[9],4,0xd9d4d039);

        HH(d,a,b,c,M[12],11,0xe6db99e5);

        HH(c,d,a,b,M[15],16,0x1fa27cf8) ;

        HH(b,c,d,a,M[2],23,0xc4ac5665);

   

        //第四轮循环计算

        II(a,b,c,d,M[0],6,0xf4292244) ;

        II(d,a,b,c,M[7],10,0x432aff97) ;

        II(c,d,a,b,M[14],15,0xab9423a7);

        II(b,c,d,a,M[5],21,0xfc93a039) ;

        II(a,b,c,d,M[12],6,0x655b59c3) ;

        II(d,a,b,c,M[3],10,0x8f0ccc92) ;

        II(c,d,a,b,M[10],15,0xffeff47d);

        II(b,c,d,a,M[1],21,0x85845dd1) ;

        II(a,b,c,d,M[8],6,0x6fa87e4f) ;

        II(d,a,b,c,M[15],10,0xfe2ce6e0);

        II(c,d,a,b,M[6],15,0xa3014314) ;

        II(b,c,d,a,M[13],21,0x4e0811a1);

        II(a,b,c,d,M[4],6,0xf7537e82) ;

        II(d,a,b,c,M[11],10,0xbd3af235);

        II(c,d,a,b,M[2],15,0x2ad7d2bb);

        II(b,c,d,a,M[9],21,0xeb86d391);

 （4）结果输出

处理完所有的512位的分组后，得到一组新的A,B,C,D的值，将这些值按ABCD的顺序级联，就得到了想要的MD5散列值。当然，输出依然要考虑内存存储的大小端问题。

3、MD5算法实现

根据前面分算法分析，接下来我们来具体实现这一算法，我们暂时不考虑字符串的分组预处理，假设只有1组，就是说长度不会超过448位。多组的炒作也是一样的，只需要增加循环计算的次数，所以我们实际从上述分析的第二步开始。

（1）初始化操作

前面我们已经提到过了，在开始MD5需要定义算法规定的数组、操作函数以及初始化4个链接变量。操作函数我们使用宏定义来实现。关于链接变量的初始化操作需要在对消息加密前操作，我们定义如下的初始化函数：

 1 /*对MD5结构体进行初始化操作*/
 2 void MD5Start(MD5Contex *context)
 3 {
 4   context->count[0]=0;
 5   context->count[1]=0;
 6    
 7   //初始化链接变量
 8   context->state[0] = 0x67452301;
 9   context->state[1] = 0xEFCDAB89;
10   context->state[2] = 0x98BADCFE;
11   context->state[3] = 0x10325476;
12 }

（2）MD5值计算

接下来我们实现MD5值得计算及结构体的更新：

 1 /*将要加密的信息传递给初始化过的MD5结构体，无返回值               */
 2 /*context：初始化过了的MD5结构体                                   */
 3 /*input：需要加密的信息，可以任意长度                                */
 4 /*inputLen：指定input的长度                                          */
 5 void MD5Update(MD5Contex *context, uint8_t *input,uint32_t inputlen)
 6 {
 7   uint32_t i = 0,index = 0,partlen = 0;
 8   index = (context->count[0] >> 3) & 0x3F;
 9   partlen = 64 - index;
10   context->count[0] += inputlen << 3;
11   if(context->count[0] < (inputlen << 3))
12   {
13     context->count[1]++;
14   }
15   context->count[1] += inputlen >> 29;
16 
17   if(inputlen >= partlen)
18   {
19     memcpy(&context->buffer[index],input,partlen);
20     MD5Process(context->state,context->buffer);
21     for(i = partlen;i+64 <= inputlen;i+=64)
22     {
23       MD5Process(context->state,&input[i]);
24     }
25     index = 0;
26   }
27   else
28   {
29     i = 0;
30   }
31   memcpy(&context->buffer[index],&input[i],inputlen-i);
32 }

MD5的主体循环部分，我们实现如下：

 1 /*对512bits信息(即block缓冲区)进行一次处理，每次处理包括四轮            */
 2 /*uint32_t *state：MD5结构体中的state[4]，用于保存信息加密的结果         */
 3 /*uint8_t *block：欲加密的512bits信息                                    */
 4 static void MD5Process(uint32_t *state, uint8_t *block)
 5 {
 6   uint32_t a = state[0];
 7   uint32_t b = state[1];
 8   uint32_t c = state[2];
 9   uint32_t d = state[3];
10   uint32_t x[64];
11 
12   MD5Decode(x,block,64);
13 
14   /*第一轮计算*/
15   FF(a, b, c, d, x[ 0], constMove[0],constTable[0][0]);
16   FF(d, a, b, c, x[ 1], constMove[1],constTable[0][1]);
17   FF(c, d, a, b, x[ 2], constMove[2],constTable[0][2]);
18   FF(b, c, d, a, x[ 3], constMove[3],constTable[0][3]);
19   FF(a, b, c, d, x[ 4], constMove[0],constTable[0][4]);
20   FF(d, a, b, c, x[ 5], constMove[1],constTable[0][5]);
21   FF(c, d, a, b, x[ 6], constMove[2],constTable[0][6]);
22   FF(b, c, d, a, x[ 7], constMove[3],constTable[0][7]);
23   FF(a, b, c, d, x[ 8], constMove[0],constTable[0][8]);
24   FF(d, a, b, c, x[ 9], constMove[1],constTable[0][9]);
25   FF(c, d, a, b, x[10], constMove[2],constTable[0][10]);
26   FF(b, c, d, a, x[11], constMove[3],constTable[0][11]);
27   FF(a, b, c, d, x[12], constMove[0],constTable[0][12]);
28   FF(d, a, b, c, x[13], constMove[1],constTable[0][13]);
29   FF(c, d, a, b, x[14], constMove[2],constTable[0][14]);
30   FF(b, c, d, a, x[15], constMove[3],constTable[0][15]);
31 
32   /*第二轮计算*/
33   GG(a, b, c, d, x[ 1], constMove[4],constTable[1][0]);
34   GG(d, a, b, c, x[ 6], constMove[5],constTable[1][1]);
35   GG(c, d, a, b, x[11], constMove[6],constTable[1][2]);
36   GG(b, c, d, a, x[ 0], constMove[7],constTable[1][3]);
37   GG(a, b, c, d, x[ 5], constMove[4],constTable[1][4]);
38   GG(d, a, b, c, x[10], constMove[5],constTable[1][5]);
39   GG(c, d, a, b, x[15], constMove[6],constTable[1][6]);
40   GG(b, c, d, a, x[ 4], constMove[7],constTable[1][7]);
41   GG(a, b, c, d, x[ 9], constMove[4],constTable[1][8]);
42   GG(d, a, b, c, x[14], constMove[5],constTable[1][9]);
43   GG(c, d, a, b, x[ 3], constMove[6],constTable[1][10]);
44   GG(b, c, d, a, x[ 8], constMove[7],constTable[1][11]);
45   GG(a, b, c, d, x[13], constMove[4],constTable[1][12]);
46   GG(d, a, b, c, x[ 2], constMove[5],constTable[1][13]);
47   GG(c, d, a, b, x[ 7], constMove[6],constTable[1][14]);
48   GG(b, c, d, a, x[12], constMove[7],constTable[1][15]);
49 
50   /*第三轮计算*/
51   HH(a, b, c, d, x[ 5], constMove[8],constTable[2][0]);
52   HH(d, a, b, c, x[ 8], constMove[9],constTable[2][1]);
53   HH(c, d, a, b, x[11], constMove[10],constTable[2][2]);
54   HH(b, c, d, a, x[14], constMove[11],constTable[2][3]);
55   HH(a, b, c, d, x[ 1], constMove[8],constTable[2][4]);
56   HH(d, a, b, c, x[ 4], constMove[9],constTable[2][5]);
57   HH(c, d, a, b, x[ 7], constMove[10],constTable[2][6]);
58   HH(b, c, d, a, x[10], constMove[11],constTable[2][7]);
59   HH(a, b, c, d, x[13], constMove[8],constTable[2][8]);
60   HH(d, a, b, c, x[ 0], constMove[9],constTable[2][9]);
61   HH(c, d, a, b, x[ 3], constMove[10],constTable[2][10]);
62   HH(b, c, d, a, x[ 6], constMove[11],constTable[2][11]);
63   HH(a, b, c, d, x[ 9], constMove[8],constTable[2][12]);
64   HH(d, a, b, c, x[12], constMove[9],constTable[2][13]);
65   HH(c, d, a, b, x[15], constMove[10],constTable[2][14]);
66   HH(b, c, d, a, x[ 2], constMove[11],constTable[2][15]);
67 
68   /*第四轮计算*/
69   II(a, b, c, d, x[ 0], constMove[12],constTable[3][0]);
70   II(d, a, b, c, x[ 7], constMove[13],constTable[3][1]);
71   II(c, d, a, b, x[14], constMove[14],constTable[3][2]);
72   II(b, c, d, a, x[ 5], constMove[15],constTable[3][3]);
73   II(a, b, c, d, x[12], constMove[12],constTable[3][4]);
74   II(d, a, b, c, x[ 3], constMove[13],constTable[3][5]);
75   II(c, d, a, b, x[10], constMove[14],constTable[3][6]);
76   II(b, c, d, a, x[ 1], constMove[15],constTable[3][7]);
77   II(a, b, c, d, x[ 8], constMove[12],constTable[3][8]);
78   II(d, a, b, c, x[15], constMove[13],constTable[3][9]);
79   II(c, d, a, b, x[ 6], constMove[14],constTable[3][10]);
80   II(b, c, d, a, x[13], constMove[15],constTable[3][11]);
81   II(a, b, c, d, x[ 4], constMove[12],constTable[3][12]);
82   II(d, a, b, c, x[11], constMove[13],constTable[3][13]);
83   II(c, d, a, b, x[ 2], constMove[14],constTable[3][14]);
84   II(b, c, d, a, x[ 9], constMove[15],constTable[3][15]);
85 
86   state[0] += a;
87   state[1] += b;
88   state[2] += c;
89   state[3] += d;
90 }

（3）输出转换

最后我们将计算所得的MD5值进行输出格式整理，时期按应有的顺序输出。

 1 /*获得最终的MD5值，无返回值                                          */
 2 /*digest：保存最终的加密串                                             */
 3 /*context：你前面初始化并填入了信息的md5结构                          */
 4 void MD5Final(MD5Contex *context, uint8_t *digest)
 5 {
 6   uint32_t index = 0,padlen = 0;
 7   uint8_t bits[8];
 8   index = (context->count[0] >> 3) & 0x3F;
 9   padlen = (index < 56)?(56-index):(120-index);
10   MD5Encode(bits,context->count,8);
11   MD5Update(context,padding,padlen);
12   MD5Update(context,bits,8);
13   MD5Encode(digest,context->state,16);
14 }

4、结论

MD5作为一种检验手段被广泛应用，特别在用户密码保存方面，因其不可逆和低碰撞的特性更是大受欢迎。我们使用自己编写的MD5算法计算一下普通的“hello world 123456789”的MD5散列值：

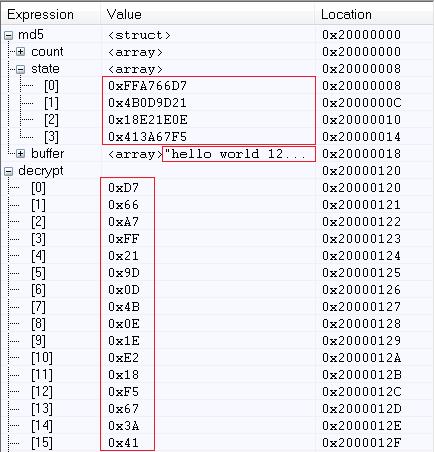
在前面我们实现了MD5算法，但是我们如果仔细分析就会发现，具体的实现代码是可以大幅度优化的，特别是在四轮计算过程中。我们如果将FF、GG、HH、II不采用宏定义，而是声明为4个函数，很明显这四个函数的声明是一样的。于是利用指针和数组可将四轮计算简化为：

 1 for(i=0;i<4;i++)
 2 {
 3   for(j=0;j<4;j++)
 4   {
 5     pF[i](a, b, c, d, x[k[i][4*j]], constMove[4*i],constTable[i][4*j]);
 6     pF[i](d, a, b, c, x[k[i][4*j+1]], constMove[4*i+1],constTable[i][4*j+1]);
 7     pF[i](c, d, a, b, x[k[i][4*j+2]], constMove[4*i+2],constTable[i][4*j+2]);
 8     pF[i](b, c, d, a, x[k[i][4*j+3]], constMove[4*i+3],constTable[i][4*j+3]);
 9   }
10 }

当然，这一优化仅是对代码层面的简化，实际的计算依然是64次，所以对算法是没有影响的。

对于中文字符的MD5散列值，则存在一个字符编码的问题，比如对中文“中国”的编码结果：

GB2312编码下的结果：CF0832DEDF7457BBCBFA00BBD87B300A

UTF-8编码下的结果：C13DCEABCB143ACD6C9298265D618A9F