算法分析| 系列4（解决递推）

Posted 2020-10-10

在前一篇文章中，我们讨论了循环的分析。许多算法本质上是递归的。当我们分析它们时，我们得到时间复杂度的递归关系。我们得到的运行时间是大小为n的输入作为n的函数，以及较小大小的输入的运行时间。例如在“ 合并排序”中，为了对给定的数组进行排序，我们将其分成两半，并递归地重复两个进程。最后我们合并结果。合并排序的时间复杂度可以写为T（n）= 2T（n / 2）+ cn。还有很多其他算法，如二进制搜索，河内塔等。

主要有三种解决复发的方法。

1）替代方法：我们猜测解，然后我们使用数学归纳来证明猜测是正确的或不正确的。

For example consider the recurrence T(n) = 2T(n/2) + n

We guess the solution as T(n) = O(nLogn). Now we use induction
to prove our guess.

We need to prove that T(n) <= cnLogn. We can assume that it is true
for values smaller than n.

T(n) = 2T(n/2) + n
    <= cn/2Log(n/2) + n
    =  cnLogn - cnLog2 + n
    =  cnLogn - cn + n
    <= cnLogn

2）重复树法：在这种方法中，我们绘制一个重复树，并计算每个级别的树所花费的时间。最后，我们总结了各级的工作。为了绘制复发树，我们从给定的复现开始，继续绘制，直到我们在各个层次之间找到一个模式。该图案通常是算术或几何系列。

For example consider the recurrence relation 
T(n) = T(n/4) + T(n/2) + cn2

           cn2
         /           T(n/4)     T(n/2)

If we further break down the expression T(n/4) and T(n/2), 
we get following recursion tree.

                cn2
           /           \      
       c(n2)/16      c(n2)/4
      /      \          /       T(n/16)     T(n/8)  T(n/8)    T(n/4) 
Breaking down further gives us following
                 cn2
            /            \      
       c(n2)/16          c(n2)/4
       /      \            /      c(n2)/256   c(n2)/64  c(n2)/64    c(n2)/16
 /    \      /    \    /    \       /    \  

To know the value of T(n), we need to calculate sum of tree 
nodes level by level. If we sum the above tree level by level, 
we get the following series
T(n)  = c(n^2 + 5(n^2)/16 + 25(n^2)/256) + ....
The above series is geometrical progression with ratio 5/16.

To get an upper bound, we can sum the infinite series. 
We get the sum as (n2)/(1 - 5/16) which is O(n2)

 

3）主方法：
主方法是获得解决方案的直接方法。主方法仅适用于以下类型的复现或可以转换为以下类型的重复。

T(n) = aT(n/b) + f(n) where a >= 1 and b > 1

有以下三种情况：

1.如果f（n）=Θ（n c）其中c <Log b a则T（n）=Θ（n Log b a）

2.如果F（N）=Θ（N ?）其中c =日志b一则T（N）=Θ（N ? log n）的

3.如果F（N）=Θ（N ?）其中c>日志b一则T（N）=Θ（F（N））

这个怎么用？
主方法主要来源于递归树法。如果我们绘制T（n）= aT（n / b）+ f（n）的递归树，我们可以看到在根处完成的工作是f（n），所有叶子的工作都是Θ（n c） c是日志b a。而递归树的高度为Log bn 在递归树方法中，我们计算完成的总工作量。如果在叶子上完成的工作多数多，那么叶子是主要的部分，我们的结果就成为树叶上的工作（情况1）。如果在叶子和根部的工作是渐进的，那么我们的结果就变成了高度乘以任何级别的工作（情况2）。如果在根处完成的工作是渐近的，那么我们的结果就会在根目录下完成（情况3）。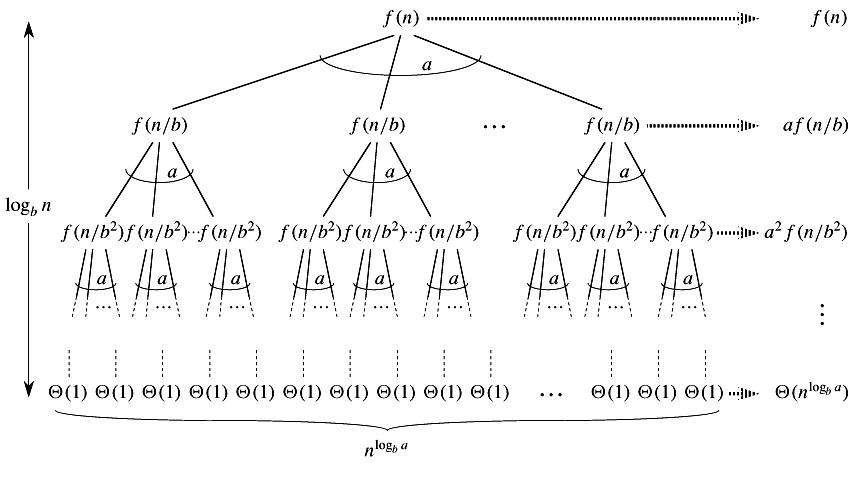

使用主方法
合并排序：T（n）= 2T（n / 2）+Θ（n）可以评估其时间复杂度的一些标准算法的示例。情况2由于c为1，Log b a]也为1.因此解为Θ（n Logn）

二进制搜索：T（n）= T（n / 2）+Θ（1）。情况2也在c为0且Log b a也为0的情况下出现。因此解为Θ（Logn）

注意：
1）使用主定理可以解决形式T（n）= aT（n / b）+ f（n）的复现。给定的三例在他们之间有一些差距。例如，使用主方法不能求解重复T（n）= 2T（n / 2）+ n / Logn。

2）情况2可以扩展为f（n）=Θ（n c Log k n）
如果f（n）=Θ（n c Log k n）对于一些常数k> = 0，c = Log b a，则T（n）=Θ（n c Log k + 1 n）