02-方法 ——课程作业01-递归练习

Posted 2020-10-10 编程小白

1.使用计算机计算组合数

（1）使用组合数公式利用n!来计算

程序设计思想：

利用递归定义一个方法jiecheng(int n)用来求一个数n的阶乘，当n>1时，返回n*jiecheng(n-1),直到n=1时，返回1。输入底数m和阶数n之后，利用该函数分别求出m和n还有m-n的阶乘，利用公式m!/n!*(m-n)!在main函数中输出结果。

程序流程图：

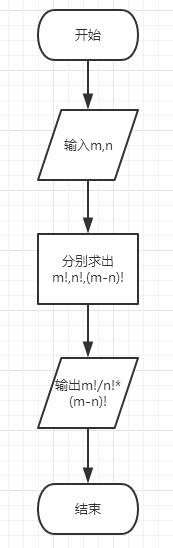
程序源代码：

 1 import java.util.Scanner;
 2 
 3 public class ZuHeShu {
 4     
 5     public static void main(String[] args) {
 6         
 7         System.out.print("请输入组合数中的底数m:");
 8         
 9         Scanner input = new Scanner(System.in);
10         
11         int import_m = input.nextInt();
12         
13         System.out.print("请输入组合数中的阶数n:");
14         
15         int import_n = input.nextInt();
16         
17         System.out.println("组合数的结果为:"+jiecheng(import_m)/(jiecheng(import_n)*jiecheng(import_m-import_n)));
18 
19     }
20 
21     public static long jiecheng(int i) 
22     
23     {    
24             
25         if(i > 1)
26         
27         {
28             
29             return i * jiecheng(i - 1);
30                 
31         }
32         
33         else
34             
35         {
36             
37             return 1;
38             
39         }
40         
41     }
42 
43 }

程序测试截图：

 

 (2)使用递推的方法用杨辉三角形计算

程序设计思想：

定义一个二维数组T存储杨辉三角形，循环赋值构造杨辉三角形：T[i][0] = 1,T[i][i] = 1,(i = 0,1,2……n)，其余每个T[i][j] =T[i - 1][j - 1] + T[i - 1][j]。则C(m,n)=T[n][k]。

程序流程图：

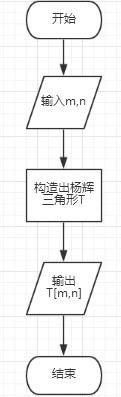
程序源代码：

 1 import java.util.Scanner;
 2 
 3 public class ZuHeShu3 {
 4     
 5      public static void main(String[] args) {
 6          
 7          System.out.print("请输入组合数中的底数m:");
 8          
 9          Scanner input = new Scanner(System.in);
10          
11          int m = input.nextInt();
12          
13          System.out.print("请输入组合数中的阶数n:");
14          
15          int n= input.nextInt();
16          
17          System.out.println("组合数的结果为:"+T(m,n));
18          
19      }
20      
21      public static int T(int m,int n){
22          
23          int[][] Y = new int[m + 1][m + 1];
24          
25          Y[0][0] = 1;
26          
27          for(int i = 0;i < m + 1;i++)
28              
29          {
30             
31             Y[i][0] = 1;
32             
33             Y[i][i] = 1;
34             
35          }
36          
37          for(int i = 2;i < m + 1;i++)
38              
39          {
40              
41              for(int j = 1;j < i;j++)
42                  
43              {
44                  
45                  Y[i][j] = Y[i - 1][j - 1] + Y[i - 1][j];
46                  
47              }
48              
49          }
50          
51          return Y[m][n];
52          
53     }
54      
55 }

程序测试截图：

(3)使用递归的方法用组合数递推公式计算

程序设计思想：

定义求组合数函数C(n,k)当k = 0或n = k时，返回1，否则，根据递推公式，C(n,k) = C(n - 1,k - 1) + C(n - 1,k)。

程序流程图：

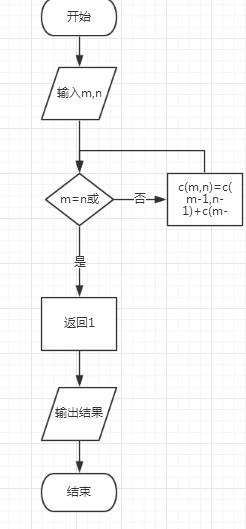
程序源代码：

import java.util.Scanner;

public class ZuHeShu2 {

    public static void main(String[] args) {
        
        System.out.print("请输入组合数中的底数m:");
        
        Scanner input = new Scanner(System.in);
        
        int import_m = input.nextInt();
        
        System.out.print("请输入组合数中的阶数n:");
        
        int import_n = input.nextInt();
        
        System.out.print("组合数的结果为:"+triangle(import_m,import_n));
        
    }

    public static long triangle(int m,int n)
    
    {
        
        if(m == n || n == 0)
            
            return 1;else
            
            return triangle(m - 1,n - 1)+triangle(m - 1,n);
        
    }

}

程序结果截图：

2.递归编程阶乘解决汉诺塔问题。

程序设计思想：

当盘子的个数n=1时，直接从A移动到C;

n>1时，可将其分为三个步骤：

(1)将上面n-1个盘子从A座移到B座上。

(2)将剩下的一个盘子从A座移到C座上。

(3)将B座上的n-1个盘子从B座移动到C座上。

其中，(1),(3)可用递归函数实现，只是从哪一个座移到哪一个座不同。

程序流程图：

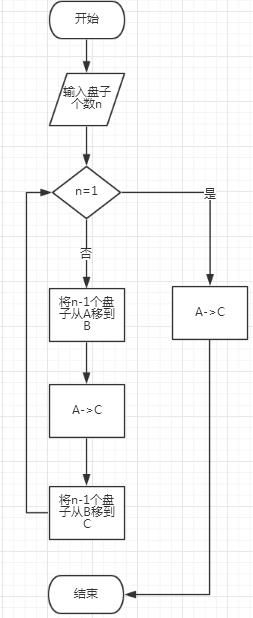
程序源代码：

import java.util.Scanner;

public class HanoiTower {

    public static void main(String[] args) {
        
        System.out.print("请输入盘子的个数:");
        
        Scanner input = new Scanner(System.in);
        
        int diskes = input.nextInt();
        
        System.out.println("挪动这"+diskes+"盘子的步骤为:");
        
        hanoi(diskes,\'A\',\'B\',\'C\');
        
    }

    public static void hanoi(int n, char a, char b, char c) 
    
    {
        
        if(n == 1)
            
        {
            
            move(a,c);
            
        }
        
        else
            
        {
            
            hanoi(n-1,a,c,b);
            
            move(a,c);
            
            hanoi(n-1,b,a,c);
            
        }
        
    }

    public static void move(char a, char c)
    
    {
        
        System.out.println(a+"-->"+c);
        
    }

}

程序结果截图：

3.使用递归方式判断某个字串是否为回文

程序设计思想：

首先比较第一个字符与最后一个字符的关系，如果相等，利用递归比较第二个与倒数第二个字符的关系，直到比较完，中间如果有一对不相等，直接退出函数并输出不是回文数。

程序流程图：

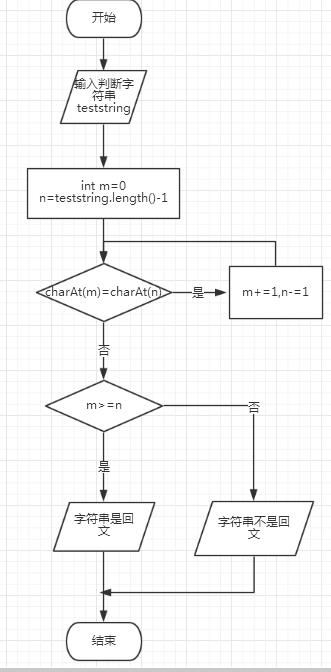
程序源代码：

import java.util.Scanner;

public class HuiWen {
    
    public static void main(String[] args) {
        
        System.out.print("请输入要判断的字符串:");
        
        Scanner input = new Scanner(System.in);
        
        String teststring = input.next();
        
        int pre = 0,end = teststring.length() - 1;
        
        if(isPalindromestring(teststring,pre,end))
            
            System.out.println(teststring+"是回文字符串!");
        
        else
            
            System.out.println(teststring+"不是回文字符串!");

    }

    public static boolean isPalindromestring(String test,int pre, int end)
    {
        
        if(pre >= end)
            
            return true;
        
        else
            
        {
            
            if(test.charAt(pre) == test.charAt(end))
                
                return isPalindromestring(test,pre+1,end-1);
            
            else
                
                return false;
            
        }
        
    }

}

程序测试截图：