Linear Regression Using Gradient Descent 代码实现

Posted 2020-10-10 照夜白

参考吴恩达<机器学习>, 进行 Octave, Python(Numpy), C++(Eigen) 的原理实现, 同时用 scikit-learn, TensorFlow, dlib 进行生产环境实现.

 

1. 原理

cost function

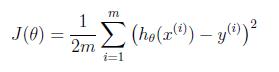
gradient descent

 

 2. 原理实现

octave

cost function

function J = costFunction(X, Y, theta)
    m = size(X, 1);
    predictions = X * theta;
    sqrErrors = (predictions - Y) .^ 2;
    J = 1 / (2 * m) * sum(sqrErrors);

 

Linear regression using gradient descent

function [final_theta, Js] = gradientDescent(X, Y, init_theta, learning_rate=0.01, max_times=1000)
    convergence = 0;
    m = size(X, 1);
    tmp_theta = init_theta;
    Js = zeros(m, 1);

    for i=1:max_times,
        tmp = learning_rate / m * ((X * tmp_theta - Y)\' * X)\';
        tmp_theta -= tmp;
        Js(i) = costFunction(X, Y, tmp_theta);
    end;

    final_theta = tmp_theta;

 

python

# -*- coding:utf8 -*-
import numpy as np
import matplotlib.pyplot as plt


def cost_function(input_X, _y, theta):
    """
    cost function
    :param input_X: np.matrix input X
    :param _y: np.array y
    :param theta: np.matrix theta
    :return: float
    """
    rows, cols = input_X.shape
    predictions = input_X * theta
    sqrErrors = np.array(predictions - _y) ** 2
    J = 1.0 / (2 * rows) * sqrErrors.sum()

    return J


def gradient_descent(input_X, _y, theta, learning_rate=0.1, 
                     iterate_times=3000):
    """
    gradient descent
    :param input_X: np.matrix input X
    :param _y: np.array y
    :param theta: np.matrix theta
    :param learning_rate: float learning rate
    :param iterate_times: int max iteration times
    :return: tuple
    """
    convergence = 0
    rows, cols = input_X.shape
    Js = []

    for i in range(iterate_times):
        errors = input_X * theta - _y
        delta = 1.0 / rows * (errors.transpose() * input_X).transpose()
        theta -= learning_rate * delta
        Js.append(cost_function(input_X, _y, theta))

    return theta, Js


def generate_data():
    """
    generate training data y = 2*x^2 + 4*x + 2
    """
    x = np.linspace(0, 2, 50)
    X = np.matrix([np.ones(50), x, x**2]).T
    y = 2 * X[:, 0] - 4 * X[:, 1] + 2 * X[:, 2] + np.mat(np.random.randn(50)).T / 25
    np.savetxt(\'linear_regression_using_gradient_descent.csv\', 
               np.column_stack((X, y)), delimiter=\',\')


def test():
    """
    main
    :return: None
    """
    m = np.loadtxt(\'linear_regression_using_gradient_descent.csv\', delimiter=\',\')
    input_X, y = np.asmatrix(m[:, :-1]), np.asmatrix(m[:, -1]).T
    # theta 的初始值必须是 float
    theta = np.matrix([[0.0], [0.0], [0.0]])
    final_theta, Js = gradient_descent(input_X, y, theta)

    t1, t2, t3 = np.array(final_theta).reshape(-1,).tolist()
    print(\'对测试数据 y = 2 - 4x + 2x^2 求得的参数为: %.3f, %.3f, %.3f\\n\' % (t1, t2, t3))
    
    plt.figure(\'theta\')
    predictions = np.array(input_X * final_theta).reshape(-1,).tolist()
    x1 = np.array(input_X[:, 1]).reshape(-1,).tolist()
    y1 = np.array(y).reshape(-1,).tolist()
    plt.plot(x1, y1, \'*\')
    plt.plot(x1, predictions)
    plt.xlabel(\'x\')
    plt.ylabel(\'y\')
    plt.title(\'y = 2 - 4x + 2x^2\')

    plt.figure(\'cost\')
    x2 = range(1, len(Js) + 1)
    y2 = Js
    plt.plot(x2, y2)
    plt.xlabel(\'iterate times\')
    plt.ylabel(\'value\')
    plt.title(\'cost function\')
    
    plt.show()
    

if __name__ == \'__main__\':
    test()

Python 中需要注意的是, numpy.array, numpy.matrix 和 list 等进行计算时, 有时会进行默认类型转换, 默认类型转换的结果, 往往不是期望的情况.

theta 的初始值必须是 float, 因为如果是 int, 则在更新 theta 时会报错.

 

测试数据:

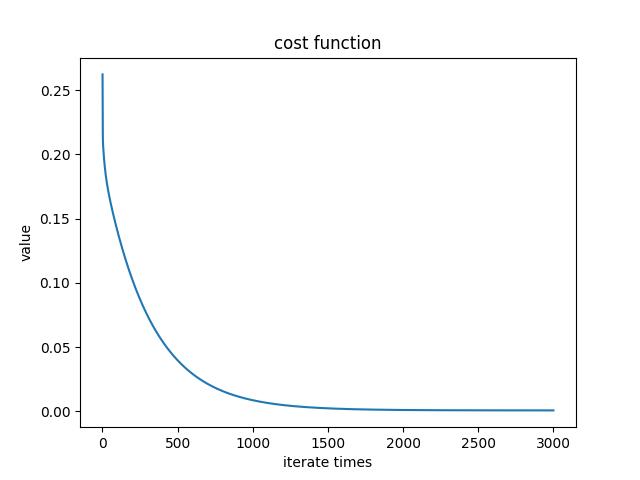
Cost function:

 

 

c++

#include <iostream>
#include <vector>
#include <Eigen/Dense>

using namespace Eigen;
using namespace std;


double cost_function(MatrixXd &input_X, MatrixXd &_y, MatrixXd &theta) {
  double rows = input_X.rows();
  MatrixXd predictions = input_X * theta;
  ArrayXd sqrErrors = (predictions - _y).array().square();
  double J = 1.0 / (2 * rows) * sqrErrors.sum();

  return J;
}


class Gradient_descent {
 public:
  Gradient_descent(MatrixXd &x, MatrixXd &y, MatrixXd &t, 
                   double r=0.1, int m=3000): input_X(x), _y(y), theta(t), 
                   learning_rate(r), iterate_times(m){}
  MatrixXd theta;
  vector<double> Js;
  void run();
 private:
  MatrixXd input_X;
  MatrixXd _y;
  double rows;
  double learning_rate;
  int iterate_times;
};


void Gradient_descent::run() {
  double rows = input_X.rows();
  for(int i=0; i < iterate_times; ++i) {
    MatrixXd errors = input_X * theta - _y;
    MatrixXd delta = 1.0 / rows * (errors.transpose() * input_X).transpose();
    theta -= learning_rate * delta;
    double J = cost_function(input_X, _y, theta);
    Js.push_back(J);
  }
}


void generate_data(MatrixXd &input_X, MatrixXd &y) {
  ArrayXd v = ArrayXd::LinSpaced(50, 0, 2);
  input_X.col(0) = VectorXd::Constant(50, 1, 1);
  input_X.col(1) = v.matrix();
  input_X.col(2) = v.square().matrix();
  y.col(0) = 2 * input_X.col(0) - 4 * input_X.col(1) + 2 * input_X.col(2);
  y.col(0) += VectorXd::Random(50) / 25;
}


int main() {
  MatrixXd input_X(50, 3), y(50, 1);
  MatrixXd theta = MatrixXd::Zero(3, 1);
  generate_data(input_X, y);
  Gradient_descent gd(input_X, y, theta);
  gd.run();
  cout << gd.theta << endl;
}

 

3. 生产环境

Python (Scikit-learn)

todo

 

Python (TensorFlow)

todo

 

C++ (dlib)

todo