字符串模式匹配KMP算法

Posted 2020-10-10 2016java

字符串模式匹配指的是，找出特定的模式串在一个较长的字符串中出现的位置。

• 朴素的模式匹配算法

很直观的可以写出下面的代码，来找出模式串在一个长字符串中出现的位置。

   /*
        朴素的模式匹配算法
        功能：字符串的模式匹配
        参数：
             s：目标串
            p：模式串
             pos：开发匹配的位置
         返回值：
            匹配成功，返回模式串在目标串的其实位置
            匹配不成功，返回-1
    */
    int match(const char * s ,const  char * p,int pos){
        int i = pos ;
       int j= 0 ;
        while(s[i] != \'\\0\' && p[j] != \'\\0\') {
         if(s[i] == p[j]) {
                 i ++ ;
                j ++ ;
           }else {
               i = i - j + 1;
                j = 0 ;
            }
       }
     
        if(p[j] == \'\\0\')
            return i - j ;
        else 
           return -1 ;
    }

 

上面的代码，s就是目标串，p是模式串，pos指定从s的什么位置开始匹配p。其实现思想也很简单：

当s[i] == p[j]时，目标串和模式串的指针都向后移动一位，进行匹配。而当s[i] != p[j]时，即匹配不成功时，将目标串和模式串的指针同时回溯，j = 0 而目标串的指针i则回溯到这轮开始的下一个位置。

朴素的模式匹配的算法复杂度是O( (n-m+1) * m)  n为目标串的长度，m为模式串长度。

从其实现思想上可以很容易的看出，造成该算法低效的地方是在，匹配不成功时主串和模式串的指针回溯上。

有没有一种算法，当模式串和主串的匹配不成功时，不用进行指针的回溯，直接进行下一轮的匹配？

• ＫＭＰ算法理解

在朴素的字符串模式匹配算法上，当遇到主串和模式串的字符不能匹配成功时，不论已经匹配了多少字符都要进行指针回溯，再开始下一轮的匹配。

这样效率是十分的低下的。ＫＭＰ算法，是在朴素的模式匹配算法的基础上，实现了匹配不成功时，不对主串指针进行回溯，使模式匹配的时间复杂度

降低为：O(n + m)。

对KMP算法的理解，在网上查找了不少资料，也看了算法导论上的描述，一直是一知半解。有次闲暇之余，想像着将模式串、主串都看着是条直线，进行了下推导，才恍然大悟。

KMP算法的核心思想是，在s[i] 和 p[j]不匹配时，不对主串进行指针回溯，而是在模式串中p中寻找k，用s[i] 和 p[k]进行下一轮的匹配。

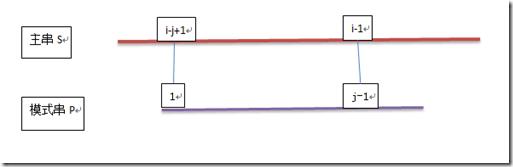
在这里，将主串 S 和模式串 P 都看成是一条直线，故而在S[i] 和 P[j] 匹配不成共时，有如下情形：

 

图1 s[i] 和 p[j] 匹配不成功

即是：p[1…j-1] == s[i-j+1,…,i-1].

p[j] 和 s[i] 不匹配，现在要在模式串p[1,…,j-1]确定一个位置k（1<= k < j-1)，用p[k]和s[i]进行下一轮匹配，那么k必须要满足以下条件：

p[1,..,k-1] == s[i-k+1, … , i-1] .

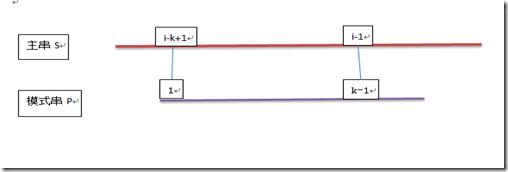
将模式串和主串都看着一条直线，那么就有下图：

图2  使用p[k]和s[i]进行下一轮匹配

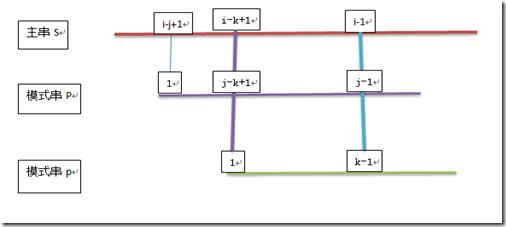
由于 1<= k < j-1，那么将两图合并起来会有什么效果呢？

从上图可以看出，当s[i]和p[j]匹配不成功时，假如能用p[k]和s[i]进行下一轮匹配，则有：

s[i-k+1], … , i-1] == p[j-k+1,…,j-1] == p[1,…,k-1] 。

就是说，当s[i] 和 p[j] 匹配不成功时，最对主串不进行指针回溯，而是用p[k]和s[i]进行匹配时，k必须满足以下条件：

p[1,…,k-1] == p[j-k+1, … , j-1]。

• KMP算法的实现

KMP算法的是对匹配的模式匹配算法的改进，在s[i]和p[j]匹配不成功时，不是对主串进行指针的回溯，而是在p[1,…,j-1]中，寻找一个p[k],

用s[i]和p[k]进行下一轮的匹配。其实现的最大问题就是如何的根据p[1,…,j-1]来求出p[k]。

在KMP算法的实现中，使用一个辅助数组next[],使用该数组保存p[j]匹配不成功时，要进行下一轮匹配的k的值.即是当s[i] 和 p[j]匹配不成功时，

用p[ next[j] ]来和s[i]进行下一轮匹配，k = next[j] .

对数组next[] 的求解，可以goolge到不少的方法，这里使用最简单的递推的方法：

首先假定next[0] = –1,那么当next[j] = k时，就有：p[0,…,j-1] == p[j-k+1,…,j-1]。

这时，若有p[k] = p[j] ，则p[0,….,k] = p[j-k+1,..,j-1,j]，从而就有next[j+1] = next[j] + 1 = k +1 .

若p[k] != p[j] ,可以看着模式串对自身进行匹配的问题，即当匹配失败的时候，k值如何确定，k = next [k] .

求数组next[ ]的实现如下：

/*
    KMP进行模式匹配的辅助函数
    模式串和主串匹配不成功时，下次和主串进行匹配的模式串的位置
*/
void continue_prefix_function(const char * p , int * next) {
    int j ;
    int k ;
    next[0] = -1 ;
    j = 0 ;
    k = -1 ;

    while(j < strlen(p) - 1) {
        if( k == -1 || p[k] == p[j]) {
            j ++ ;
            k ++ ;
            next[j] = k ;
        }else {
            k =next[k] ;
        }
    }
}

　　

知道了当模式串和主串匹配不成功时，下一个和主串匹配的字符在模式串中的位置，在朴素的模式匹配的基础上很容易的写出KMP算法的代码如下：

 

/*
    运用KMP算法的字符串模式匹配
    在主串和模式串匹配不成功时，不对主串指针进行回溯，
    例如用next[j],来指定下一次和主串进行匹配的模式串的位置
*/
int match_kmp(const char * s ,const char * p,int pos) {
    int next[11] ;
    int i = pos ;
    int j = 0 ;
    continue_prefix_function(p,next) ;
    while(s[i] != \'\\0\' && p[j] != \'\\0\') {
        if(s[i] == p[j]) {
            i ++ ;
            j ++ ;
        }else {
            if(next[j] == -1) {
                i ++ ;
                j = 0 ;
            }
            else {
                j = next[j] ;
            }
        }
    }
    if(p[j] == \'\\0\')
        return i - j ;
    else
        return -1 ;
}

 

• 总结