数论四大定理（转）

Posted 2020-10-10

emmm...，手动转载。

数论四大定理：

1.威尔逊定理

2.欧拉定理

3.孙子定理（中国剩余定理）

4.费马小定理

 

1.威尔逊定理

在初等数论中威尔逊给出了判定一个自然数是否为素数的充分必要条件：

 

当且仅当p为素数时：( p -1 )! ≡ -1 ( mod p )

或者这么写( p -1 )! ≡ p-1 ( mod p )

或者说

若p为质数，则p能被(p-1)!+1整除

 

2.欧拉定理

欧拉定理：若n,a为正整数，且n,a互质，即gcd(a,n) = 1，则a^φ(n) ≡ 1 (mod n)

欧拉函数（符号：φ(n) ）：欧拉函数是求 （小于n的数 ）中 （与n互质的数 ）的数目

或者说  欧拉函数是求 1到n-1 中 与n互质的数 的数目

 

如果n是质数，那么1到n-1所有数都是与n互质的，所以φ(n) = n-1。

如果n是合数，自己算吧。

 

欧拉公式：e^ix  =  cosx  +  isinx ，把x用π带进去，变成e^iπ + 1 = 0。（虽然还没用过，先记录下来吧）

 

3.中国剩余定理（孙子定理）

中国剩余定理给出了以下的一元线性同余方程组：

　

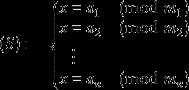
中国剩余定理说明：假设整数m1,m2, ... ,mn两两互质，则对任意的整数：a1,a2, ... ,an，方程组 (S)有解

  

4.费马小定理

假如p是质数，若p不能整除a，则 a^(p-1) ≡1（mod p），若p能整除a，则a^(p-1) ≡0（mod p）。

或者说，若p是质数，且a,p互质，那么 a的(p-1)次方除以p的余数恒等于1。

 

 

费马大定理，又被称为“费马最后的定理”，由法国数学家费马提出。

它断言当整数n >2时，关于x, y, z的方程 x^n + y^n = z^n 没有正整数解。

被提出后，经历多人猜想辩证，历经三百多年的历史，最终在1995年被英国数学家安德鲁·怀尔斯证明。