luogu 3374,3368树状数组1,2

Posted 2020-10-10 Emine

树状数组1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某一个数加上x

2.求出某区间每一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x k 含义：将第x个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4

输出样例#1：

14
16

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

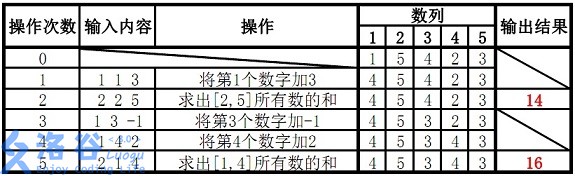
故输出结果14、16

 1 #include<cstdio>
 2 #include<iostream>
 3 #include<cstring>
 4 #include<algorithm>
 5 #define maxn 500005
 6 using namespace std;
 7 int n,m,a[maxn],c[maxn];
 8 inline int lowbit(int x){return x&(-x);}
 9 inline void add(int pos,int x){
10     while(pos<=n){
11         c[pos]+=x;
12         pos+=lowbit(pos);
13     }
14 }
15 inline int getsum(int pos){
16     int tmp=0;
17     while(pos>0){
18         tmp+=c[pos];
19         pos-=lowbit(pos);
20     }
21     return tmp;
22 }
23 int main(){
24     scanf("%d%d",&n,&m);
25     for(int i=1;i<=n;i++){
26         scanf("%d",&a[i]);
27         add(i,a[i]);
28     }
29     int a,b,c;
30     for(int i=1;i<=m;i++){
31         scanf("%d%d%d",&a,&b,&c);
32         if(a==1) add(b,c);
33         else if(a==2) printf("%d\n",getsum(c)-getsum(b-1));
34     }
35     return 0;
36 }

树状数组2

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某区间每一个数数加上x

2.求出某一个数的和

输入输出格式

输入格式：

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含2或4个整数，表示一个操作，具体如下：

操作1： 格式：1 x y k 含义：将区间[x,y]内每个数加上k

操作2： 格式：2 x 含义：输出第x个数的值

输出格式：

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入样例#1：

5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4

输出样例#1：

6
10

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

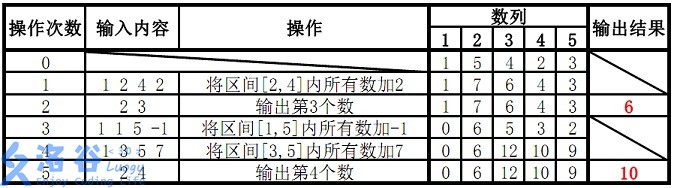
故输出结果为6、10

 1 #include<cstdio>
 2 #include<iostream>
 3 #include<cstring>
 4 #include<algorithm>
 5 #define maxn 500005
 6 using namespace std;
 7 int n,m,a[maxn],c[maxn],d[maxn];
 8 inline int lowbit(int x){return x&(-x);}
 9 inline void add(int pos,int x){
10     while(pos<=n){
11         c[pos]+=x;
12         pos+=lowbit(pos);
13     }
14 }
15 inline int getsum(int pos){
16     int tmp=0;
17     while(pos>0){
18         tmp+=c[pos];
19         pos-=lowbit(pos);
20     }
21     return tmp;
22 }
23 int main(){
24     scanf("%d%d",&n,&m);
25     for(int i=1;i<=n;i++){
26         scanf("%d",&a[i]);
27         d[i]=a[i]-a[i-1];
28         add(i,d[i]);
29     }
30     int q,x,y,k;
31     for(int i=1;i<=m;i++){
32         scanf("%d",&q);
33         if(q==1){
34             scanf("%d%d%d",&x,&y,&k);
35             d[x]+=k;add(x,k);
36             d[y+1]-=k;add(y+1,-k);
37         }
38         else if(q==2){
39             scanf("%d",&x);
40             printf("%d\n",getsum(x));
41         }
42     }
43     return 0;
44 }