Locality-sensitive hashing
Posted rsapaper
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Locality-sensitive hashing相关的知识,希望对你有一定的参考价值。
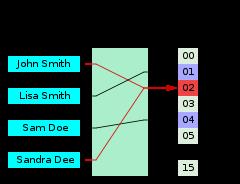
A hash function that maps names to integers from 0 to 15. There is a collision between keys "John Smith" and "Sandra Dee".、、
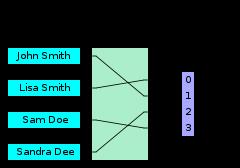
A minimal perfect hash function for the four names shown
https://en.wikipedia.org/wiki/Hash_function
【hash the input items so that similar items are mapped to the same buckets with high probability 相似的入同桶】
Locality-sensitive hashing (LSH) is a method of performing probabilistic dimension reduction of high-dimensional data. The basic idea is to hash the input items so that similar items are mapped to the same buckets with high probability (the number of buckets being much smaller than the universe of possible input items). This is different from the conventional hash functions, such as those used in cryptography, as in this case the goal is to minimize the probability of "collision" of every item.[18]
One example of LSH is MinHash algorithm used for finding similar documents (such as web-pages):
Let h be a hash function that maps the members of A and B to distinct integers, and for any set S define hmin(S) to be the member x of S with the minimum value of h(x). Then hmin(A) = hmin(B) exactly when the minimum hash value of the union A ∪ B lies in the intersection A ∩ B. Therefore,
- Pr[hmin(A) = hmin(B)] = J(A,B). where J is Jaccard index.
In other words, if r is a random variable that is one when hmin(A) = hmin(B) and zero otherwise, then r is an unbiased estimator of J(A,B), although it has too high a variance to be useful on its own. The idea of the MinHash scheme is to reduce the variance by averaging together several variables constructed in the same way.
【MinHash 减小方差--变异】
zh.wikipedia.org/wiki/散列函數
【性能不佳的散列函数表意味着查找操作会退化为费时的线性搜索】
Hash Tables
Hash functions are used in hash tables,[1] to quickly locate a data record (e.g., a dictionary definition) given its search key (the headword). Specifically, the hash function is used to map the search key to a list; the index gives the place in the hash table where the corresponding record should be stored. Hash tables, also, are used to implement associative arrays and dynamic sets.[2]
Typically, the domain of a hash function (the set of possible keys) is larger than its range (the number of different table indices), and so it will map several different keys to the same index. So then, each slot of a hash table is associated with (implicitly or explicitly) a set of records, rather than a single record. For this reason, each slot of a hash table is often called a bucket, and hash values are also called bucket listing[citation needed] or a bucket index.
Thus, the hash function only hints at the record\'s location. Still, in a half-full table, a good hash function will typically narrow the search down to only one or two entries.
People who write complete hash table implementations choose a specific hash function—such as a Jenkins hash or Zobrist hashing—and independently choose a hash-table collision resolution scheme—such as coalesced hashing, cuckoo hashing, or hopscotch hashing.
散列表是散列函数的一个主要应用,使用散列表能够快速的按照关键字查找数据记录。(注意:关键字不是像在加密中所使用的那样是秘密的,但它们都是用来“解锁”或者访问数据的。)例如,在英语字典中的关键字是英文单词,和它们相关的记录包含这些单词的定义。在这种情况下,散列函数必须把按照字母顺序排列的字符串映射到为散列表的内部数组所创建的索引上。
散列表散列函数的几乎不可能/不切实际的理想是把每个关键字映射到唯一的索引上(参考完美散列),因为这样能够保证直接访问表中的每一个数据。
一个好的散列函数(包括大多数加密散列函数)具有均匀的真正随机输出,因而平均只需要一两次探测(依赖于装填因子)就能找到目标。同样重要的是,随机散列函数不太会出现非常高的冲突率。但是,少量的可以估计的冲突在实际状况下是不可避免的(参考生日悖论或鸽洞原理)。
在很多情况下,heuristic散列函数所产生的冲突比随机散列函数少的多。Heuristic函数利用了相似关键字的相似性。例如,可以设计一个heuristic函数使得像FILE0000.CHK, FILE0001.CHK, FILE0002.CHK,等等这样的文件名映射到表的连续指针上,也就是说这样的序列不会发生冲突。相比之下,对于一组好的关键字性能出色的随机散列函数,对于一组坏的关键字经常性能很差,这种坏的关键字会自然产生而不仅仅在攻击中才出现。性能不佳的散列函数表意味着查找操作会退化为费时的线性搜索。
【通过平均用同一方式构造的许多随机变量,从而减少方差】
【The idea of the MinHash scheme is to reduce this variance by averaging together several variables constructed in the same way.】
The Jaccard similarity coefficient is a commonly used indicator of the similarity between two sets. For sets A and B it is defined to be the ratio of the number of elements of their intersection and the number of elements of their union:
This value is 0 when the two sets are disjoint, 1 when they are equal, and strictly between 0 and 1 otherwise. Two sets are more similar (i.e. have relatively more members in common) when their Jaccard index is closer to 1. The goal of MinHash is to estimate J(A,B) quickly, without explicitly computing the intersection and union.
Let h be a hash function that maps the members of A and B to distinct integers, and for any set S define hmin(S) to be the minimal member of S with respect to h—that is, the member x of S with the minimum value of h(x). Now, applying hmin to both A and B, and assuming no hash collisions, we will get the same value exactly when the element of the union A ∪ B with minimum hash value lies in the intersection A ∩ B. The probability of this being true is the ratio above, and therefore:
- Pr[ hmin(A) = hmin(B) ] = J(A,B),
That is, the probability that hmin(A) = hmin(B) is true is equal to the similarity J(A,B), assuming randomly chosen sets A and B. In other words, if r is the random variable that is one when hmin(A) = hmin(B) and zero otherwise, then r is an unbiased estimator of J(A,B). r has too high a variance to be a useful estimator for the Jaccard similarity on its own, because {\\displaystyle r}
【 measurable functions on a measurable space 


http://infolab.stanford.edu/~ullman/mmds/book.pdf
【局部敏感哈希 思路 多次随机hash运算 相似的 进同一桶】
One general approach to LSH is to “hash” items several times, in such a way that similar items are more likely to be hashed to the same bucket than dissimilar items are. We then consider any pair that hashed to the same bucket for any of the hashings to be a candidate pair. We check only the candidate pairs for similarity. The hope is that most of the dissimilar pairs will never hash to the same bucket, and therefore will never be checked. Those dissimilar pairs that do hash to the same bucket are false positives; we hope these will be only a small fraction of all pairs. We also hope that most of the truly similar pairs will hash to the same bucket under at least one of the hash functions. Those that do not are false negatives; we hope these will be only a small fraction of the truly similar pairs.



以上是关于Locality-sensitive hashing的主要内容,如果未能解决你的问题,请参考以下文章
