10.6 simulated match

Posted 2020-10-09 yodel

 

 well the code is the best language.

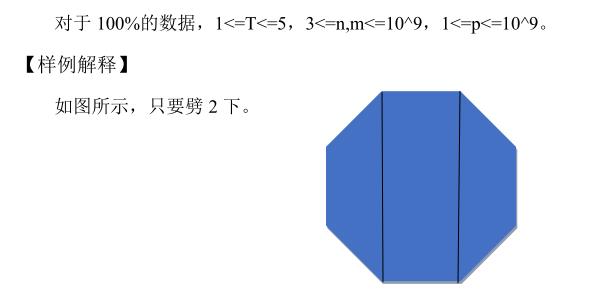
#include <cstdio>
#define ll long long
using namespace std;
ll lt1,lt2,ans,t,n,m,p;
#define init(a) freopen(a".in","r",stdin);freopen(a".out","w",stdout); 
#define ct   register int
#define cr   register char
#define g()   getchar()
#define fr(a,b,c)   for(ct a=b;a<=c;a++)
int read(){ct f=1,x=0;cr c=g();
   for(;c<\'0\'||c>\'9\';c=g())if(c==\'-\')f=-1;
   for(;\'0\'<=c&&c<=\'9\';c=g())x=(x<<1)+(x<<3)+(c^48);return x*f;}
int main(){init("handicraft");t=read();//read the sum of the data
    while (t--){//make a loop in order to read each group of data
        n=read(),m=read(),p=read();//read sum_of_edges,wanted_polygon\'s edge_sum,and wanted_sum_of_polygon
        //this is a mathematical problem,we need to search for law in order to solve this problem
        //after calculus,we can find that if we cut a polygon with m_edge froma polygon with n_edge,there is three possible case
        
        //1:we cut across two endpoint,we can find that we divide the polygon into two polygons
        //    respectly is a polygon with n-m+2_edge and a polygon with m_edge
        //for example:we cut a quadrangle and divide it into two triangle 4-3+2=3,after several try ,we find that this formula is true
        //now ,let\'s formulate it ,n-> n-m+2 and m(cross two endpoint)
        
        //2:we cut across only one endpoint, we can find that we divide the polygon into two polygons
        //    respectly is a polygon with n-m+3_edge and a polygon with m_edge
        //for example:we cut a quadrangle and divide it into one quadrangle and one triangle 4-3+3=4,after several try, we find that this formula is true
        //now ,let\'s formulate it ,n-> n-m+3 and m(cross one endpoint)
        
        //3:we cut across no endpoint ,we can find that we divide the polygon into two polygons
        //    respectly is a polygon with n-m+4_edge and a polygon with m_edge
        //for example:we cut a quadrangle and divide it into one pentagon and one triangle 4-3+4=5,after several try, we find that this formula is true
        //now ,let\'s formulate it ,n-> n-m+4 and m(cross no end point)
        
        //now let\'s arrange these formula:
        //case 1 cut cross two endpoint:n-> n-m+2 and m
        //case 2 cut cross one endpoint:n-> n-m+3 and m
        //case 3 cut cross no  endpoint:n-> n-m+4 and m
        
        //if we want p m_edge_polygon,we need at least n=(p-1)(m-4)+m  (we need cut at least p times)
        //so,we need to respectly deal with these different cases 
        lt1=m*p-(p-1)*4;//the same as (p-1)(m-4)+m
        lt2=m*p-(p-1)*2;//the same as (p-1)(m-2)+m
        //here we have two case 
        
        //case 1: m=3:lt2
        //for example:we want to cut two triangle,and we would like to use p-1 knives to cut it in order to make it satisfy
        //!!!!(OF COURSE!JOJ,we find that cut p-1 knives can always make best solution)!!!!
        //we need at most (p-1)(m-2)+m_edge_polygon
        //p-1=1,m-2=1,1+3=4.validate by hand,we can easily find that this is true.
        //by cutting from quadrangle,we need 2-1=1 knife(cross two endpoint)to cut it into two triangle
        //and by cutting from triangle(at most 4)is also OK(cross one endpoint)to cut it into three triangle
        //after several try,we get this formula
        
        //case 2: m>=4:lt1
        //for example:we want to cut two triangle,and we would like to use p-1 knives to cut it in order to make it satisfy
        //we need at least (p-1)(m-4)+m_edge_polygon p-1=1,m-4=0 0+4=4.validate by hand,we can easily find that this is true
        //by cutting from quadrangle,we need 2-1=1 knife(cross no endpoint)to cut it into two quadrangles
        
        //one exmample is not enough,this time ,we use standard input to have a try
        //we want to cut three quadrangles,and we would like to use p-1 knives to cut it in order to make it satisfy
        //we need at least (p-1)(m-4)+m_edge_polygon p-1=2,m-4=0 0+4=4,validate by hand,we can easily find that this is true
        //here is a octagon ,is bigger than 4,so it\'s really enough
        //we need to  cut p-1=2 knives(cross two endpoint)to cut it into three quadrangles
        if(n<=lt1) ans=lt1-n+p-1;
        //here if n<=lt1,m must bigger than three,if not lt1 can be a negative and n<=lt1 can\'t be satisfied 
        //if we can\'t reach the order(at least n=(p-1)(m-4)+m)
        //we need to make it satisfy at first 
        //how can we do this, we need to cut a triangle from this polygon(just means cut off an endpoint)
        //for example: if we cut off an endpoint from polygon, we find that the rectangle become pentagon 
        //it get a new edge!!!(QAQ),by this we only need to cut (lt1-n)_endpoint to make it satisfy
        //after do this ,we only need to cut p-1_times more to divide it into  p m_edge_polygon 
        //it\'s a really possible way(IAI)
        else if(n<=lt2) ans=p-1;
        //or ,just means that it satisfies the order or m==3
        //if this satisfy the order for triangle(at most (p-1)(m-2)+m),
        //here are two case:
        //case 1:m==3 and we only need to cut p-1 knives,because of the satisfied order
        //case 2:m>=4 and it has satisfied the order:lt1,we only need to cut p-1 knives because of the satisfied order 
        else ans=p;
        //or ,here only have one case:m==3 and order for triangle can\'t be satisfied
        //we need to cut an extra knife to make it satisfy
        //for example:cut two triangle from one pentagon,5>(p-1)(m-2)+m=4,so we need to cut it to a quadrangle
        //it\'s easy to prove ,if we want to reduce edge, one knife is enough(you can have a try)
        //so we need p-1+1=p knives 
        printf("%lld\\n",ans);}//out the answer
}

 

 I think my explain is quite understandable ,if you can\'t understand ,you can contact me.

---

 

 

 

 

#include <cstdio>
#define ll long long
#define MN 1005
using namespace std;
bool u[MN];ll f[MN],ans;int pri[MN],n,prin;
#define init(a) freopen(a".in","r",stdin);freopen(a".out","w",stdout); 
#define ct   register int
#define cr   register char
#define g()   getchar()
#define fr(a,b,c)   for(ct a=b;a<=c;a++)
int read(){ct f=1,x=0;cr c=g();
   for(;c<\'0\'||c>\'9\';c=g())if(c==\'-\')f=-1;
   for(;\'0\'<=c&&c<=\'9\';c=g())x=(x<<1)+(x<<3)+(c^48);return x*f;}
int main(){init("textile");
    //well,let me explain the meaning of the problem 
    //  the problem is to ask we to divide a number into different cases,
    //and calculate total_number of different_smallest_common_multiple
    //why it ask smallest_common_multiple?
    //for example:there are two group:group_one:2 and group_two:3,after group_one finish working,they should still work
    //(because group_two has not stopped),after group_two finish working, they should still work
    //(because group_one\'s finish_time became 4),after group_one finish working ,they should still work 
    //(because group_two\'s finish_time became 6),At 6,group_one and group_two both stop working
    //the total time is 6,after several try,we find this rule
    
    ct i,j,k;n=read();//read the total_number of machine_workers
    fr(i,2,n){//make a loop from 2 to n
        if(!u[i])//if u[i] has not been marked
          pri[++prin]=i;//just means this is a prime and add it into the prime_array
        for(j=1;i*pri[j]<=n;++j){//make a loop to find a number\'s prime_factor
            u[i*pri[j]]=true;//if this divide_method is allowed(<=n),just mark it true
            if(i%pri[j]==0)break;//if i is not a prime_number just break
        }
    }
    for(f[0]=i=1;i<=prin;++i)//make a iterator in order to visit each prime_factor
        for(j=n;j>=pri[i];--j)
            for(k=pri[i];k<=j;k*=pri[i])//make two iterator to divide the number
            f[j]+=f[j-k];//change one prime_factor can make different smallest multiple
            //so we calculate answer in this way(here we use array:f to calculate the answer)
            //this use the knapsack_problem\'s thinking
            //here we calculate the final solution by cumulate 1~n\'s case_num
    fr(i,0,n)ans+=f[i];//cumulate the answer\'s sum
    printf("%lld",ans);//out the answer
}

 

 

 

 

---

 

 

 

 

#include <cstdio>
#define MN 1000005
using namespace std;
int t,n,a[MN],ne[MN];
#define init(a) freopen(a".in","r",stdin);freopen(a".out","w",stdout); 
#define ct   register int
#define cr   register char
#define g()   getchar()
#define fr(a,b,c)   for(ct a=b;a<=c;a++)
int read(){ct f=1,x=0;cr c=g();
   for(;c<\'0\'||c>\'9\';c=g())if(c==\'-\')f=-1;
   for(;\'0\'<=c&&c<=\'9\';c=g())x=(x<<1)+(x<<3)+(c^48);return x*f;}
int main(){init("filament");
    ct i,j;t=read();//read the sum of the datas
    while (t--){//make a loop in order to read each data
        n=read();//read the length of the filament
        fr(i,1,n)//make a loop in order to read each point of the filament
        a[i]=read();
        ne[0]=-1;//initializate the first num as a border
        //we use KMP(Knuth-Morris-Pratt Algorithm)\'s thinking
        //to solve this problem, we only need to work out the n-next[n]
        //well ,it\'s easy to prove n-next[n]is the smallest loop_part
        //if you don\'t know kmp,you can visit my blog to study KMP.
        //or maybe you don\'t know KMP well,have a look at my blog too
        

        for(i=1,j=-1;i<=n;ne[i++]=++j)
            for(;j>-1&&a[j+1]!=a[i];j=ne[j]);//work out the array:next
        printf("%d\\n",n-ne[n]);//out the answer
    }
}