汕头市队赛SRM 20 T2不净的圣杯

Posted 2020-10-09 友人A

不净的圣杯 SRM 20

背景

        作为一张BUG级别的卡，官方打算把它修改得人畜无害一些……

        虽然名字还没想好，但是能力大概是对敌方所有单位造成d点伤害，d为自己牌组中所有卡的编号的最大公约数。这无疑是一个全新的技能类型，决定一出，负责“自动编辑卡组”系统的工程师们发愁了，要如何让AI把这一鬼畜设定考虑进去呢？我们现在只能假定每张牌被编进卡组的概率是相等的，工程师们想知道d的期望值。

描述

        给n个数，问随机从中挑出一些数（大于等于1个）后，挑出数字的期望gcd。输出期望值乘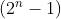并对1e9+7取模后的值。

输入格式

        第一行两个正整数n,m。

        第二行n个不超过m的正整数。

输出格式

        一个整数，期望值乘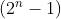并对1e9+7取模后的值。

样例输入

3 5
1 2 3

样例输出

10

数据范围

测试点	n	m
1	10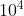
2	10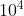
3	10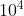
4	20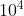
5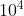
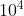6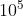
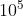7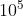
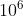8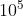
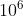9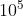
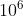10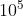

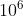样例解释

        答案为1*5+2*1+3*1=10

—————————————————————————

这题一眼看去很明显的就是莫比乌斯反演（主观臆断QAQ

 

g（x）就是以x为gcd的方案数（子集数） 

f（x）就是以x（及x的倍数）为gcd的方案数

f（x）可以暴力求O（mlogm） 可以先求出T(x)就是以是x倍数的数的个数

f（x）=2^T(x)-1 至于莫比乌斯函数mu（x）可以线性筛 这样之后及可以求答案辣

那个乘上2^n-1其实就是为了抵消期望而已 题目就是求gcd和

#include<cstdio>
#include<cstring>
#include<algorithm>
#define LL long long
const int M=1e6+7,mod=1e9+7;
int read(){
    int ans=0,f=1,c=getchar();
    while(c<\'0\'||c>\'9\'){if(c==\'-\') f=-1; c=getchar();}
    while(c>=\'0\'&&c<=\'9\'){ans=ans*10+(c-\'0\'); c=getchar();}
    return ans*f;
}
LL ans,g[M],n,m,k,w[M],t[M];
LL ly[M],f[M],vis[M],mu[M],cnt,p[M];
void prepare(){
    ly[0]=1; for(int i=1;i<=m;i++) ly[i]=ly[i-1]*2%mod;
    mu[1]=1;
    for(int i=2;i<=m;i++){
        if(!vis[i]){p[++cnt]=i;mu[i]=-1;}  
        for(int j=1;j<=cnt&&i*p[j]<=m;j++){
            vis[i*p[j]]=1;  
            if(i%p[j]) mu[i*p[j]]=-mu[i];  
            else{mu[i*p[j]]=0; break;}  
        }
    } 
}
int main(){
    n=read(); m=read();
    prepare();
    for(int i=1;i<=n;i++) k=read(),w[k]++;
    for(int i=1;i<=m;i++){
        for(int j=i;j<=m;j+=i) t[i]=(t[i]+w[j])%mod;
        f[i]=(ly[t[i]]-1+mod)%mod;
    }
    for(int i=1;i<=m;i++) for(int k=1;k*i<=m;k++) g[i]=(g[i]+mu[k]*f[k*i]%mod)%mod;
    for(int i=1;i<=m;i++) ans=(ans+g[i]*i%mod)%mod;
    printf("%lld\\n",(ans+mod)%mod);
    return 0;
}

View Code