归并排序

Posted 2020-07-01 code bless me

定义

所谓归并排序是指将两个或两个以上有序的数列（或有序表），合并成一个仍然有序的数列（或有序表）。

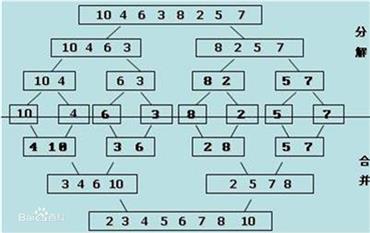
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

伪代码：

MERGE（A，p,q,r）
　　N1←q-p+1
　　N2←r-q
　　Creat arrays L[1……n1+1] and R[1….n2+1]
　　For i←1 to n1
　　　　Do l[i]←A[p+i-1]
　　For j←1 to n2
　　　　Do R[j]←A[q+j]
　　L[n1+1]←∞
　　R[n2+1]←∞
　　i←1
　　j←1
　　for k←p to r
	do if Li]<=R[j]
	　　then A[k]←l[j]
	　　　　　　i←i+1	
	else A[k]←R[j]
		j←j+1

MERGE_SORT(A,p,r)
　　If p<r
　　Then q←[(p+r)/2]
　　　　MERGE_SORT(A,p,q)
　　　　MERGE_SORT(A,p+1,q)
　　　　MERGE_SORT(A,p,q,r)
C语言代码

 1 #include<stdio.h>
 2 #include<stdlib.h>
 3 
 4 void merge(int *a, int p, int q, int r);
 5 void mergeSort(int *a, int p, int r);
 6 
 7 int main(void)
 8 {
 9     int i;
10     int a[10] = {2,6,8,9,7,5,0,1,3,4};
11 
12     mergeSort(a, 0, 9);
13     for(i = 0; i < 10; i ++)
14         printf("%d ", a[i]);
15 
16     return 0;
17 }
18 
19 void merge(int *arr, int p, int q, int r)
20 {
21     int n1 = q - p + 1;
22     int n2 = r - q;
23     int i, j, k = p;
24     int *arr_L, *arr_R;
25 
26     arr_L = (int *)malloc(n1 * sizeof(int));
27     arr_R = (int *)malloc(n2 * sizeof(int));
28     for(i = 0; i < n1; i ++)
29         arr_L[i] = arr[p + i];
30     for(j = 0; j < n2; j ++)
31         arr_R[j] = arr[q + j + 1];
32 
33     i = j = 0;
34 
35     while(i < n1 && j < n2)
36     {
37         if(arr_L[i] <= arr_R[j])
38             arr[k ++] = arr_L[i ++];
39         else
40             arr[k ++] = arr_R[j ++];
41     }
42     while(i < n1)
43         arr[k ++] = arr_L[i ++];
44     while(j < n2)
45         arr[k ++] = arr_R[j ++];
46 }
47 
48 void mergeSort(int *a, int p, int r)
49 {
50     int q = 0;
51 
52     if(p < r)
53     {
54         q =(int)(p + r) / 2;
55         mergeSort(a, p, q);
56         mergeSort(a, q + 1, r);
57         merge(a, p, q, r);
58     }
59 }
复杂度

时间复杂度为O(nlogn) 这是该算法中最好、最坏和平均的时间性能。空间复杂度为 O(n)

比较操作的次数介于(nlogn) / 2和nlogn - n + 1。

赋值操作的次数是(2nlogn)。归并算法的空间复杂度为：0 (n)

归并排序比较占用内存，但却是一种效率高且稳定的算法。