简单的动态规划，数字三角形，以及做题思路。

Posted 2020-10-09 zzozz

链接

一句话题目：给出一个n层的三角形，每个位置有一个数字，到达后可获得，求到达最低层能达到的最大数字和。

 

题目分析：

首先我们考虑能不能用搜索做，因为对于一个坐标，我们只有向下的左边或者右边。对于一个三角形我们进行特殊的处理，比如下面的三角形我们可以处理成

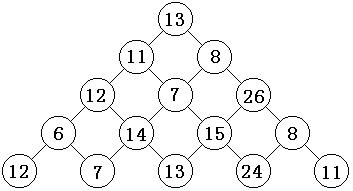
13

11  8

12  7   26

6   14 15  8

12 7   13  24 11

如果我们到达了一个位置（i，j）我们继续向下可以到达（i+1，j+1）和（i+1，j）；

那么搜索的代码：

#include <cstdio>

const int maxn = 1010;

int n, ans, cnt;
int val[maxn][maxn];

void dfs(int i,int j){
    if (i == n+1){
        if (cnt > ans) ans = cnt;
        return ;
    }
    cnt += val[i][j];
    dfs(i+1, j+1);dfs(i+1, j);
    cnt -= val[i][j];
} 
int main(){
    scanf("%d", &n);
    for (int i = 1;i <= n;i ++) 
        for (int j = 1;j <= i;j ++) scanf("%d", &val[i][j]);
    dfs(1, 1);
    printf("%d", ans);
}

复杂度是2^n很明显超时（题目中n为1000）；

我们看一个简单的情况比如我们在（i，j）这个位置，这个位置是由（i-1，j）转移过来，我们已经求出了所有的（i，j）以下的点我们向上返回到（i-1，j）这个位置，我们就向下达到（i，j+1）我们发现（i，j）可以到达（i+1，j+1）并且（i，j+1）也可以到达（i+1，j+1）；那么这个点我们就计算了两次，导致效率低下，如果我们用一个数组表示到达（i，j）能得到的最大数值，就可以不用重复计算，这样就相当于把每个点都遍历一遍，复杂度就是（（1+n）*n/2） 就不会超时了，我们把这个方法，叫做记忆化，而整个方法叫做记忆化搜索。

下面看代码：

#include <cstdio>
#include <cstring>
#include <iostream>

const int maxn = 1010;

using namespace std;

int n;
int val[maxn][maxn], f[maxn][maxn];

int dfs(int i,int j){
    if (f[i][j] != -1) return f[i][j];
    if (i == n+1) return f[i][j] = val[i][j];
    return f[i][j] = max(dfs(i+1, j+1), dfs(i+1, j)) + val[i][j];
}
int main(){
    memset(f, -1, sizeof(f));
    scanf("%d", &n);    
    for(int i = 1;i <= n;i ++)
        for (int j = 1;j <= i;j ++) scanf("%d", &val[i][j]); 
    printf("%d", dfs(1,1));
} 

但是因为递归比递推本身慢所以我们平时都不写递归，可以写成递推。我们前面讲到的是f[i][j]表示从（i，j）出发能达到的最大值，现在我们换种方式，用f[i][j]表示从（1,1）出发到达（i，j）的最大值，因为我们发现（i，j）可以从（i-1，j）和（i-1，j-1）转移过来所以我们按照f[i][j] = max(f[i-1][j-1], f[i-1][j]) + val[i][j];可以得到当前点的最大值，那么因为我们在计算f[i][j]的时候一定要保证f[i-1][j-1]和f[i-1][j]已经计算过。所以我们可以采用顺推的方法就是从上向下推。下面看代码：

#include <cstdio>
#include <cstring>
#include <iostream>

const int maxn = 1010;

using namespace std;

int n, ans;
int val[maxn][maxn], f[maxn][maxn];

int main(){
    scanf("%d", &n);    
    for (int i = 1;i <= n;i ++)
        for (int j = 1;j <= i;j ++) scanf("%d", &val[i][j]);
    for (int i = 1;i <= n;i ++)
        for (int j = 1;j <= i;j ++){
            if (j == 1) f[i][j] = val[i][j] + f[i-1][j];
            else if (j == n) f[i][j] = val[i][j] + f[i-1][j-1];
            else f[i][j] = max(f[i-1][j], f[i-1][j-1]) + val[i][j];
        }
    for (int i = 1;i <= n;i ++) ans = max(ans, f[n][i]);
    printf("%d", ans); 
} 

考虑一个新的思想，从上到下求最大值，可以转换为从最后一排出发到达第一层的最大值，那么对于（i，j）可以从（i+1， j+1）和（i+1， j）过来，那么可以将整个递推倒过来写，就可以 不用最后一个for循环了。

代码：

#include <cstdio>
#include <iostream>

const int maxn = 1010;

using namespace std;

int n;
int f[maxn][maxn], val[maxn][maxn];

int main(){
    scanf("%d", &n);
    for (int i = 1;i <= n;i ++)
        for (int j = 1;j <= i;j ++) scanf("%d", &val[i][j]);
    for (int i = n;i >= 1;i --)
        for (int j = 1;j <= i;j ++)
            f[i][j] = max(f[i+1][j], f[i+1][j+1]) + val[i][j];
    printf("%d", f[1][1]);
    return 0;
} 

下面对于动态规划进行总结：

1.首先定义状态，考虑有关的变量，然后进行定义

2.找出转移方程

3.进行优化，一般就是状态优化和转移优化。