UVALive 6916Punching Robot 组合数学

Posted 2020-10-09 可是我不配

题意：

给了你一个n*m的地图

上面有k个守卫 守卫周围的8个格子是不能经过的

我们只能向右走或者向下走

问你从左上角到右下角有多少种走法

 

思路：

首先 我们对于一个没有守卫的n*m的地图

从左上角到右下角的走法是C(n+m,n)

因为我们从左上角走到右下角一共需要n+m步 

我们在每一个格子都可以向下或者向右

所以我们需要选择其中的n步向右走 其他m步向下走

如果这个格子有守卫 那么我们经过这个格子的走法就都不行了

但是如果我们一个一个算的话 会有很多条路算重复

就像图中的这条路径就被我们删掉了两次 实际情况可能更多

 

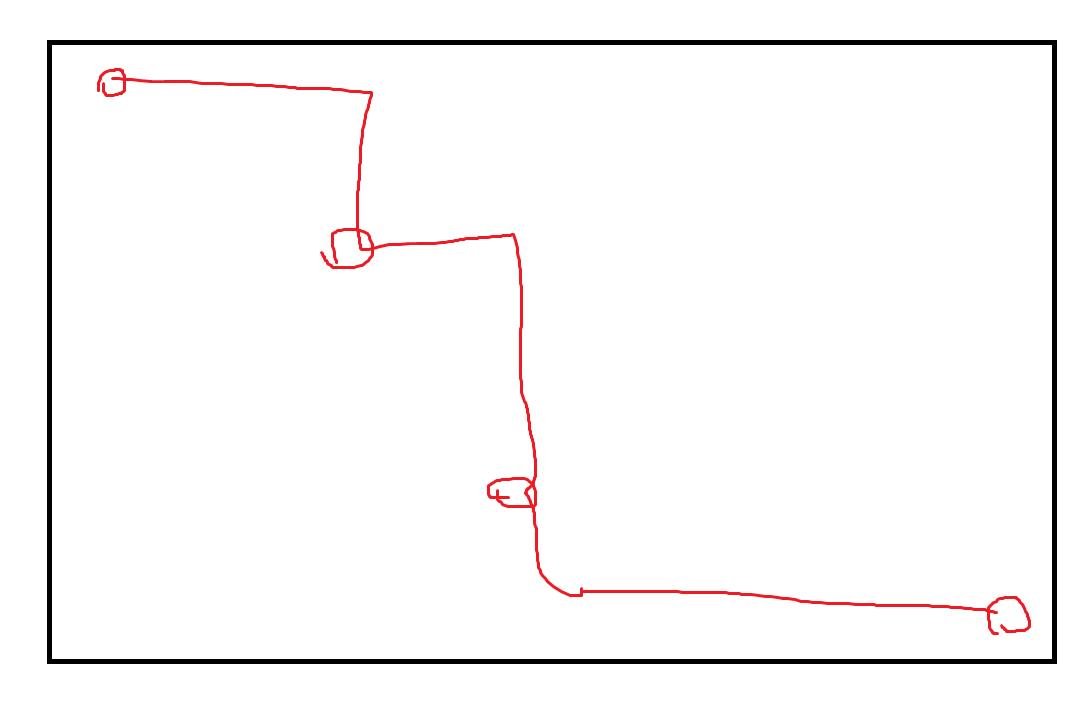
所以我们先对守卫的坐标去重排序

排完序之后 我们在计算某一个坐标的时候 就要去掉之前计算过的答案

 

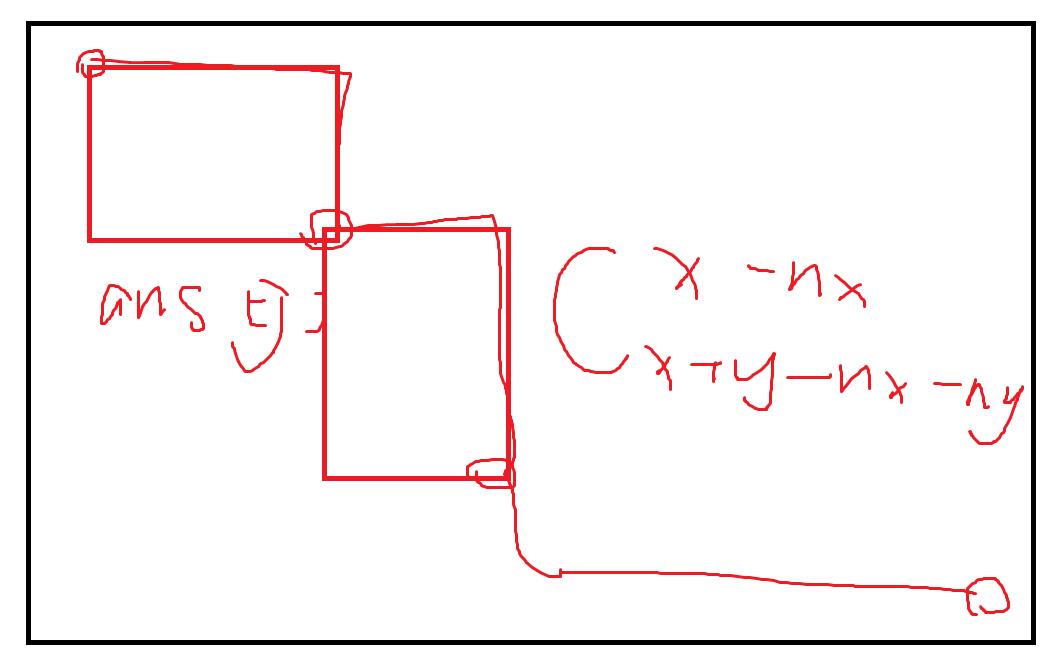
ans的含义是到达当前点的可行解是多少 一直算到最后就好了

 

一开始用的预处理Cmn 但是mod太小 mod以后的逆元处理不出来了

所以只能用费马小定理处理逆元了……

 

  1 #include<bits/stdc++.h>
  2 #define cl(a,b) memset(a,b,sizeof(a))
  3 #define debug(a) cerr<<#a<<"=="<<a<<endl
  4 using namespace std;
  5 typedef long long ll;
  6 typedef pair<int,int> pii;
  7 
  8 const int maxn=2e6+10;
  9 const int mod=997;
 10 
 11 ll fac[maxn],f[maxn];
 12 
 13 int dx[10]={0,0,0,1,-1,1,-1,-1,1};
 14 int dy[10]={0,1,-1,0,0,1,-1,1,-1};
 15 
 16 ll quick_pow(ll a,ll n)
 17 {
 18     ll ans=1;
 19     while(n)
 20     {
 21         if(n%2) ans=1ll*ans*a%mod;
 22         a=1ll*a*a%mod;
 23         n>>=1;
 24     }
 25     return ans;
 26 }
 27 
 28 ll inv(ll a)
 29 {
 30     return quick_pow(a,mod-2);
 31 }
 32 
 33 void init()
 34 {
 35     fac[0]=1;
 36     for(int i=1;i<maxn;i++)
 37     {
 38         fac[i]=1ll*fac[i-1]*i%mod;
 39     }
 40 }
 41 
 42 ll C(ll a,ll b)
 43 {
 44     ll ans=1;
 45     if(a<b || b<0) return 0;
 46     while(a&&b)
 47     {
 48         ll aa=a%mod,bb=b%mod;
 49         if(aa<bb) return 0;;
 50         ans = 1ll*ans*fac[aa]%mod * inv(1ll*fac[bb]*fac[aa-bb]%mod)%mod;
 51         a/=mod,b/=mod;
 52     }
 53     return ans;
 54 }
 55 
 56 template<typename T>
 57 void print(T vec) //打印
 58 {
 59     for(auto it:vec)
 60     {
 61         cout<<it.first<<" "<<it.second<<endl;
 62     }
 63 }
 64 
 65 template<typename T> void solve(T &vec)
 66 {
 67     sort(vec.begin(),vec.end()); //排序
 68     auto over=unique(vec.begin(),vec.end()); //去重
 69     vec.erase(over,vec.end());
 70 }
 71 
 72 int main()
 73 {
 74     int T,cas=1;
 75     scanf("%d",&T);
 76     init();
 77     while(T--)
 78     {
 79         vector<pii>st;
 80         st.clear();
 81         int n,m,k;
 82         scanf("%d%d%d",&n,&m,&k);
 83         n--,m--;
 84         st.push_back({n,m});
 85         int x,y,nx,ny;
 86         for(int i=0;i<k;i++)
 87         {
 88             scanf("%d%d",&x,&y);
 89             x--,y--;
 90             for(int j=0;j<9;j++)
 91             {
 92                 if(x+dx[j]<=n&&y+dy[j]<=m)
 93                 {
 94                     st.push_back({x+dx[j],y+dy[j]});
 95                 }
 96             }
 97         }
 98         solve(st);
 99         vector<ll>ans(st.size(),0);
100         for(int i=0;i<st.size();i++)
101         {
102             x=st[i].first;
103             y=st[i].second;
104             ans[i]=C(x+y,x);
105             for(int j=0;j<i;j++)
106             {
107                 nx=st[j].first;
108                 ny=st[j].second;
109                 ans[i]=((ans[i]-(ans[j]*C(x+y-nx-ny,x-nx)))%mod+mod)%mod;
110             }
111         }
112         printf("Case #%d: %lld\\n",cas++,*ans.rbegin());
113     }
114     return 0;
115 }/*
116 
117 5
118 4 10 2
119 3 3
120 2 8
121 3 5 1
122 2 3
123 5 5 0
124 10 9 3
125 9 3
126 6 8
127 3 4
128 100000 100000 1
129 50000 50000
130 
131 */