[神经网络与深度学习]使用神经网络识别手写数字

Posted 2020-10-09

1.1 感知器

 

 

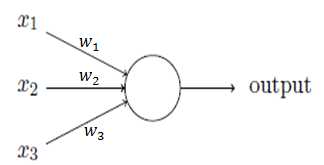
感知器的输出为：

 

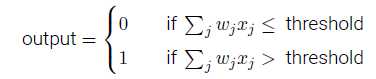
wj为权重，表示相应输入对输出的重要性；

threshold为阈值，决定神经元的输出为0或1。

也可用下式表示：

 

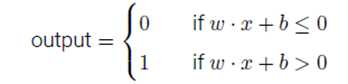
其中b=-threshold，称为感知器的偏置。

通过学习算法，能够自动调整人工神经元的权重和偏置。

1.2 S型神经元

 

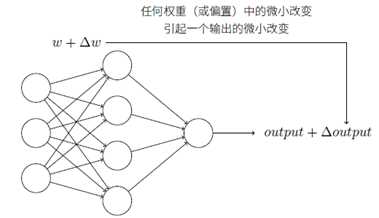
感知器模型中，权重或偏置的微小变化可能导致输出是0和1的不同，使得调试权重或偏置的工作变得困难。使用S型神经元可以改进这种情况。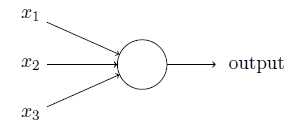

S型神经元的输出为：

 

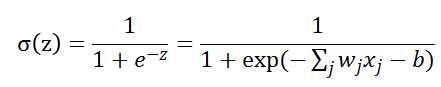
上面函数形状如下图：

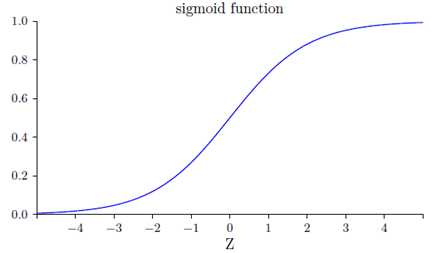
Z为很大的正数时，输出为1；Z为很大的负数时，输出为0。

当权重和偏置发生微小的变化时，输出的变化是：

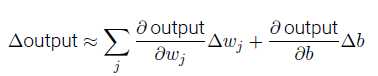
Δoutput 是一个反映权重和偏置变化的线性函数。这一线性使得选择权重和偏置的微小变化来达到输出的微小变化的运算变得容易。

1.3 神经网络的结构

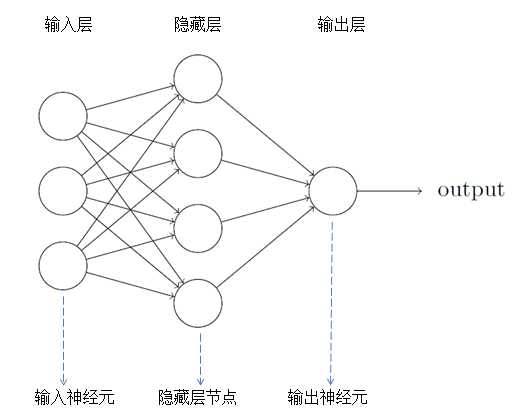
   神经网络一般分为输入层，隐藏层和输出层。需要注意两点：1.有些神经网络包含着多个隐藏层；2.输出层的输出神经元可以为1个或多个。例如手写数字识别，它的输出可以为“0”到“9”，一共10个输出神经元。

1.4 梯度下降法

      当设计好一个神经网络的架构时，它的权重和偏置是未知的。需要用梯度下降法去寻找这些权重w和偏置b的值。

      训练集中，输入为x，输出为y(x)，定义一个代价函数:

 

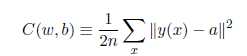
      N是训练输入数据的个数，a表示输入为x时的输出，由x，w和b决定。C称为二次代价函数，或均方误差或MSE。如果a的值约等于y(x)（当前输出等于目标输出），则说明网络的权重和偏置设计符合要求。

      因此，我们的目标是使C(w,b)约等于0，并求出相应的权重和偏置。

 

 

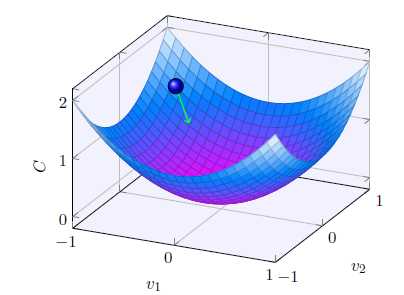
 假设C是一个只有两个变量v1和v2的函数，我们的目标是将小球移动到最低点。上图中，当球体在v1和v2分别移动很小的量时，C的变化为：

  

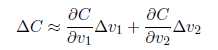
 定义v的变化向量为：,梯度向量为：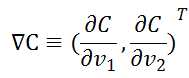

 此时，我们选择v的变化量为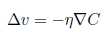：   。所以C的变化量可以表示为：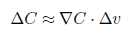

 则C的变化量为一个恒小于0的值，可以使得C一直减小，从而找到C的最小值。（为一个很小的正数，称为学习速率）   

   

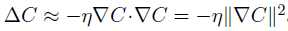
 此时，球体的位置表示为：

 

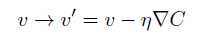
总结一下，梯度下降算法的工作方式就是重复计算梯度?C，然后沿着相反的方向移动，沿着山谷“滚落”。

1.5 神经网络中的梯度下降法

   在神经网络中使用梯度下降法，主要的目标是寻找能够使下列方程的代价取得最小值的权重wk和偏置bl。

 

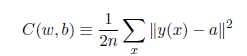
更新规则为：

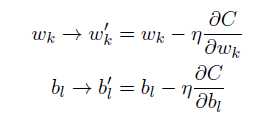
因为每一次更新总需要利用到所有的训练样本，为加快训练时间，可使用随机梯度下降法，主要的思想就是随机选取小量训练样本来计算梯度变量。

算法：

Step1.随机选择m个训练样本，称为小批量数据。

Step2.假设这m个训练样本的梯度下降量等于整个训练样本的梯度下降量。

 

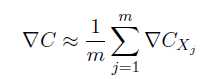
Step3.使用这些数据更新神经网络的权重和偏置。

 

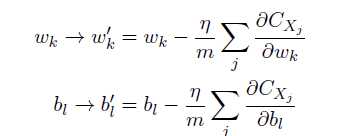
Step4.再挑选另一随机选定的小批量数据去训练。直到用完所有的训练样本，称为一个训练迭代期。

1.6 手写数字识别的实现

  首先，将一个手写数字图像分成一个m×n个部分。例如将图像分成28×28个区域，则输出层包含了784（28×28）个输入神经元，其神经网络的架构如图。

 

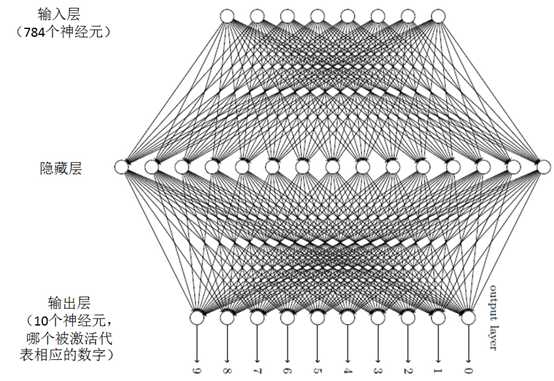
   对于输入神经元，当黑色部分占这个区域超过50%时，则这个神经元的值为1，否则为0。

   对于输出神经元，一共有10个。当第一个神经元被激活，它的输出为1时，即识别这个数字为0。