算法-最长回文子串(Manacher算法)

Posted 2020-10-09

今天在lintCode做了一道面试题，非常的简单，利用常规的方法计算起来非常的简答，但是有意思的就是挑战项。我们先来看看题：

题意：

给出一个字符串（假设长度最长为1000），求出它的最长回文子串，你可以假
定只有一个满足条件的最长回文串。

样例：

给出字符串 "abcdzdcab"，它的最长回文子串为 "cdzdc"。

挑战：

O(n2) 时间复杂度的算法是可以接受的，如果你能用 O(n) 的算法那自然更好

常规的方法在这里就不展示，这里最主要的是展示Manacher算法。

1.Manacher算法

  首先说明一下，Manacher算法能够使得在O(n)的时间复杂度下找到最长的回文子串。

  (1).Manacher算法的概述

     Manacher算法只能解决长度为奇数的字符串，所以Manacher算法利用了一个比较巧妙的方法来同时解决长度为奇数或者偶数的字符串。Manacher算法通过转换字符串来实现的，例如：原来的字符串：abc，经过转换得到：#a#b#c#，这样原来的字符串长度不管是奇数还是偶数，最终转换都能够得到一个长度为奇数的字符串。

   其次，Manacher算法通常还需要一个数组(我们假设是，len数组)来记录每一个字符在原字符串中的回文字符串的最大长度，其实实际上是，该字符在原来的字符串中得到的最长回文字符串的一半长度。

  例如：aba，经过转换得到：#a#b#a#，b能得到的最长回文字符串是：#a#b#a#，我们假设b的下标是i，得到的最长字符串的第一个字符下标是left，最后一个字符的下标是right那么b对应的值是：right - i + 1；

  同时，我们还能知道的是，i对应的字符得到的最大回文子串长度是：len[i] - 1,例如：上面的例子，b的下标是3，所以len[3] = 4,那么b对应的回文字符串aba，长度恰好是len[3] - 1 = 3。这个是为什么呢？我们假设原来的字符串为oldString(没有经过转换的)，转换过后的字符串为newString，假设oldString长度为length，那么newString的长度就为2 * length + 1,所以得到的字符串长度肯定为奇数。对于newString中的第i个字符对应的回文字符串，长度肯定为2 * len[i] - 1(这个你们可以简单的去举例子测试一下)，同时，经过观察得知，2 * len[i] - 1个字符中，肯定有len[i]个是#,其余的才是正常的符号，因为在所有的回文字符串中#的个数总是与其他符号的个数相差为1。

  (2).len数组的计算

    首先，我们从左往右计算len[i]，当我们计算len[i]时，len[j]已经计算完毕(0 < j < i)。

    我们假设，在已经计算了的字符当中取得最长回文子串的右端点的最大值(该回文字符串不一定是最长的回文字符串，只是要求该回文字符串右端下标最大)，假设最大值为rightIndex，并且设置该回文子串中心的位置是centerIndex，那么分为两种情况：

   A.i < rightIndex

     我们假设以centerIndex为中心，与i对应的是j。如图：

  

 

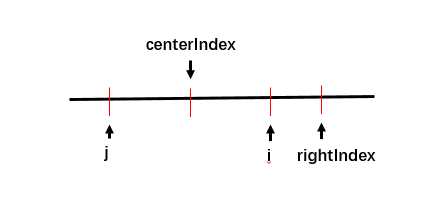
   我们知道的是，以centerIndex为中心，回文字符串能达到rightIndex，那么此时有分为两种情况：

   如果i + len[j] < P,也就是说，以j为中心的回文字符串在以centerInde为中心的回文字符串内部，此时可以得到以j为中心的回文字符串与以i为中心的回文字符串是相同的，为什么呢？因为他们在以centerIndex为中心的回文字符串的内部。所以可以得到的是，len[i] = len[j]。

  如果i + len[j] >= P的话，也就是说，以i为中心的回文字符串有一部分在以centerIndex为中心的回文字符串的外部，此时外部这一部分需要我们一个一个的计算。

 B.i > rightIndex

  如果i > rightIndex的话，那就说明，以i为中心的回文字符串一点都没有匹配。所以需要我们一个一个的匹配了。

2.代码

 1 public static String longestPalindrome(String string) {
 2 
 3         //-----------------------------------
 4         //转换字符串
 5         StringBuilder stringBuilder = new StringBuilder();
 6         stringBuilder.append("#");
 7         for (int i = 0; i < string.length(); i++) {
 8             stringBuilder.append(string.charAt(i));
 9             stringBuilder.append("#");
10         }
11         //-----------------------------------
12         int rightIndex = 0;
13         int centerIndex = 0;
14         //求len中的最大
15         int answer = 0;
16         //answer最大时的中心
17         int index = 0;
18         int len[] = new int[stringBuilder.length() ];
19         for (int i = 1; i < stringBuilder.length(); i++) {
20             //当rightIndex > i，那么我们就在rightIndex - i 与len[2 * centerIndex - i](len[j])，取得最小值
21             //因为当i + len[j] < rightIndex时，我们就把len[i]更新为len[j]
22             //但是如果i + len[j] >= rightIndex时，我们暂且将len[i]定更新为rightIndex - i,超出的部分需要我们一个一个的匹配
23             if (rightIndex > i) {
24                 len[i] = Math.min(rightIndex - i, len[2 * centerIndex - i]);
25             } else {
26                 len[i] = 1;
27             }
28             //一个一个匹配
29             //要么是超出的部分，要么是i > rightIndex
30             while(i - len[i] >= 0 && i + len[i] < stringBuilder.length() && stringBuilder.charAt(i - len[i]) == stringBuilder.charAt(i + len[i])) {
31                 len[i]++;
32             }
33             //当 len[i] + i > rightIndex,我们需要更新centerIndex和rightIndex
34             //至于为什么会这样做，理解一下rightIndex和centerIndex的含义
35             if(len[i] + i > rightIndex) {
36                 rightIndex = len[i] + i;
37                 centerIndex = i;
38             }
39             if(len[i] > answer) {
40                 answer = len[i];
41                 index = i;
42             }
43         }
44         //截取字符串
45         //为什么index - answer + 1,因为len[i] - 1才是原来的回文字符串长度，而answer记录的是len中最大值
46         return stringBuilder.substring(index - answer + 1, index + answer).replace("#", "");
47     }