堆排序算法剖析

Posted 2020-10-09 花弄影

1.将待排序列以一个完全二叉树存储，设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。

 　

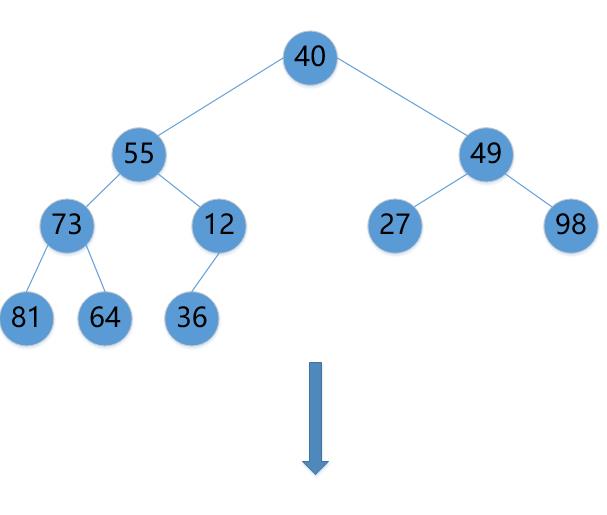
2.第一趟排序，从二叉树的最后一个根节点（有步骤1可知是值为12的节点）开始，调整当前节点所在的堆，使当前节点大于所有子节点的值，最终得到的堆是最大根堆。

(1)12->36

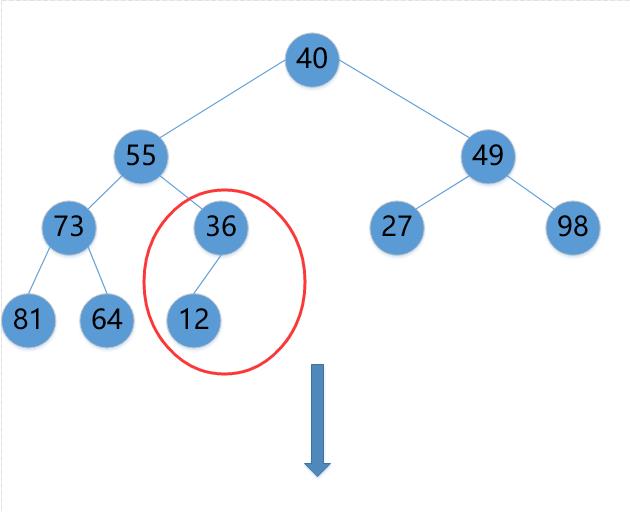
(2)73->81

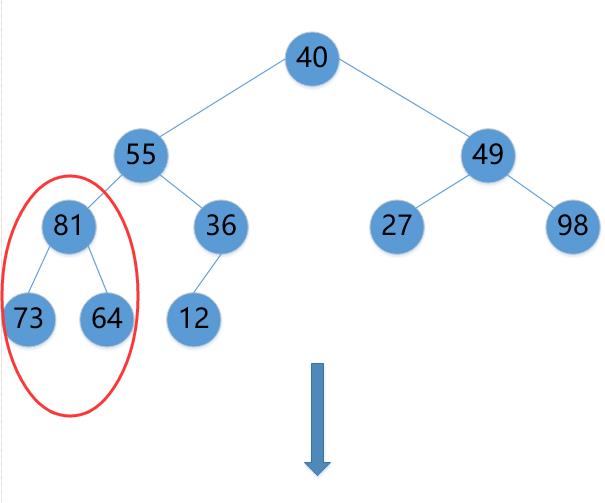
(3)49->98

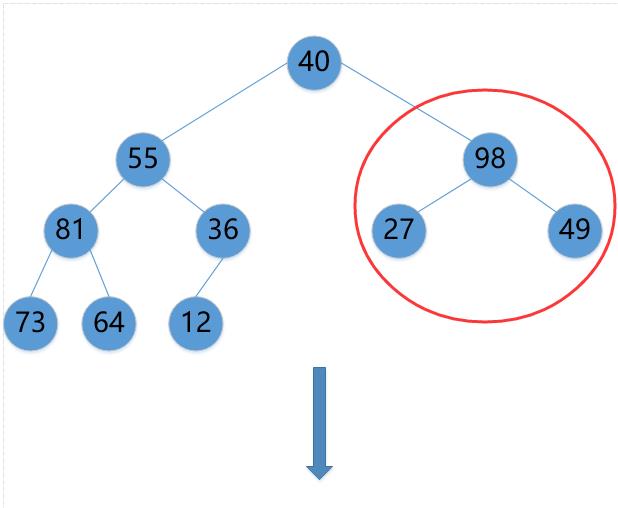
(4)55->81->73

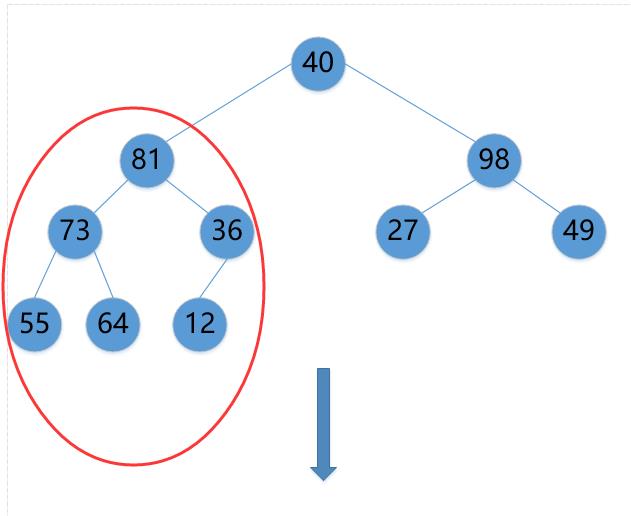
(5)40->98->49

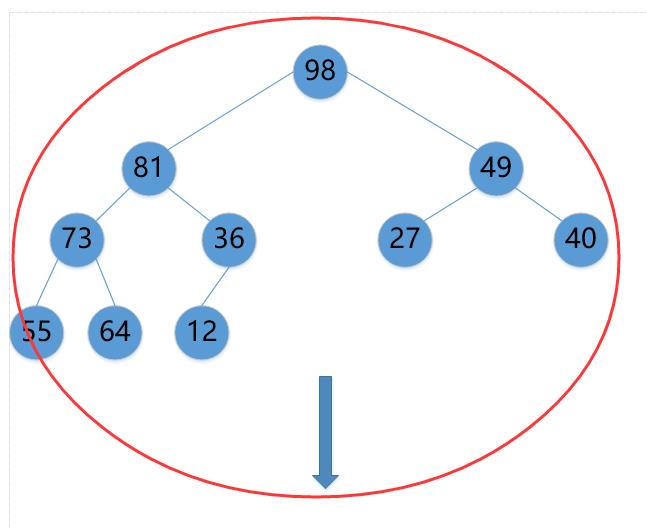
3.第二趟排序，每趟排序后，待排序列中的最大值将被移动到根节点，将根节点元素与待排序列中最后一个元素交换位置，红色元素表示已经排好的序列，红色元素不参与下轮的排序过程

(1)98->12

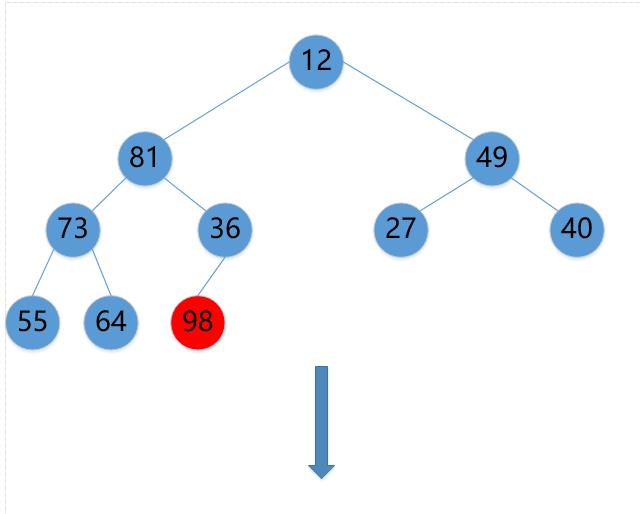
(2)12->81->73->64

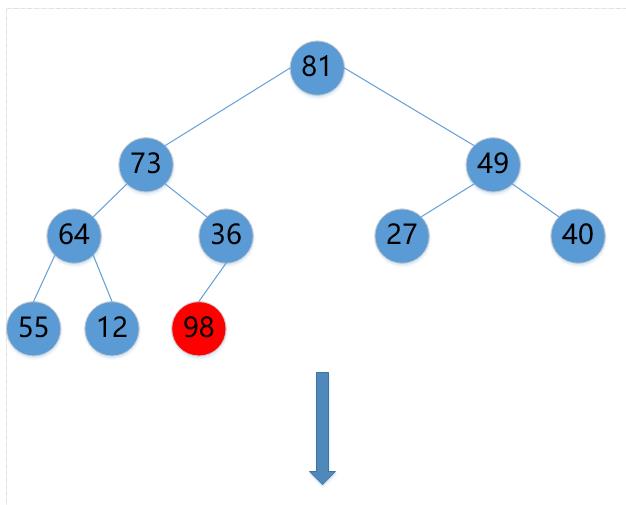
(3)81->12

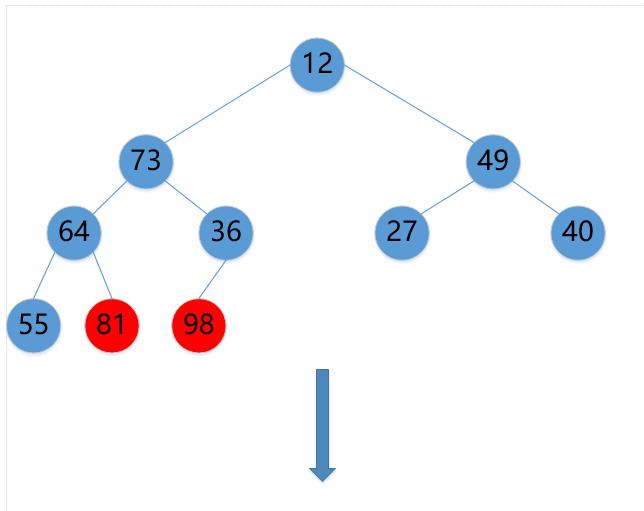
(4)12->73->64->55

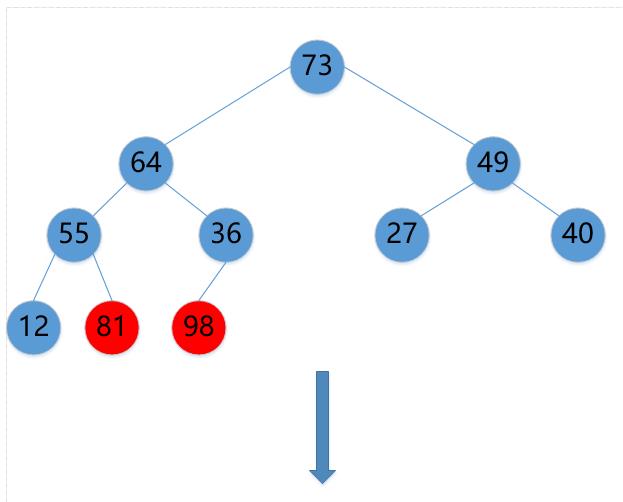
(5)73->12

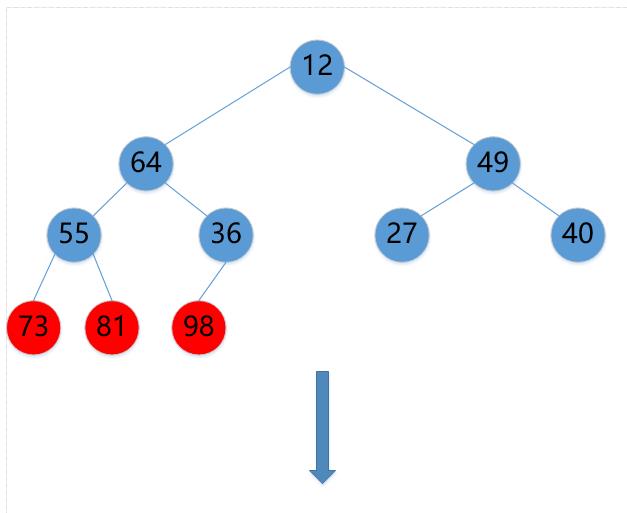
(6)12->64->55

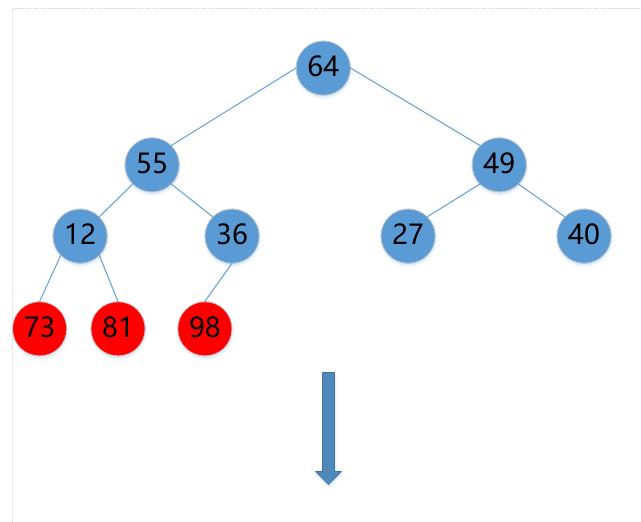
(7)64->40

 

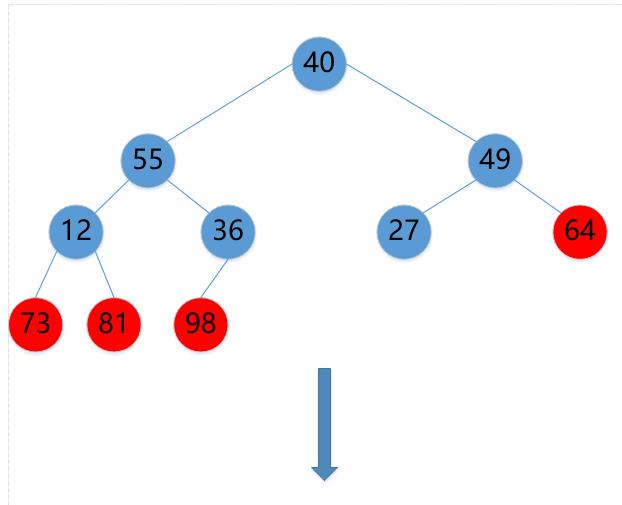
(8)40->55

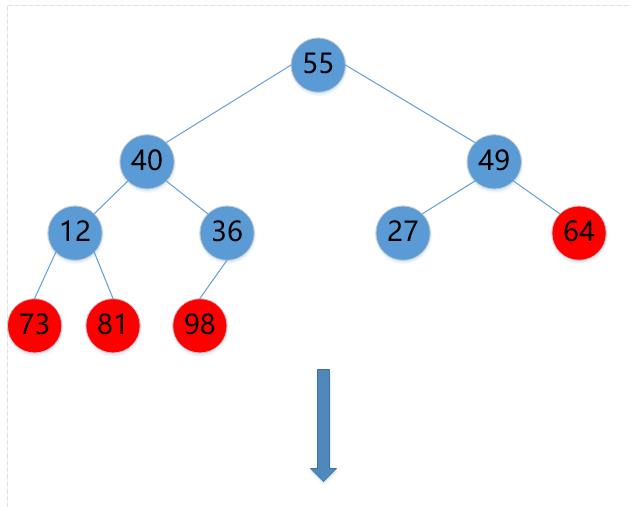
(9)55->27

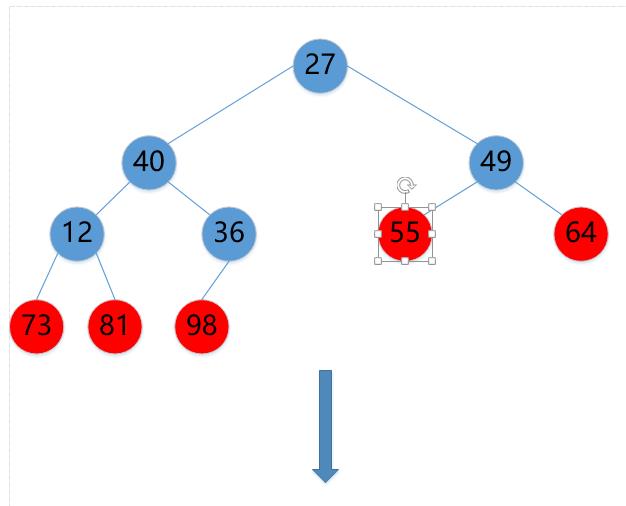
(10)27->49

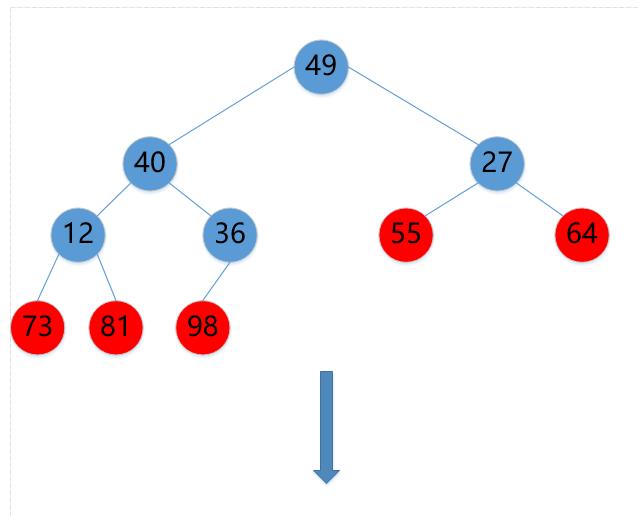
(11)49->36

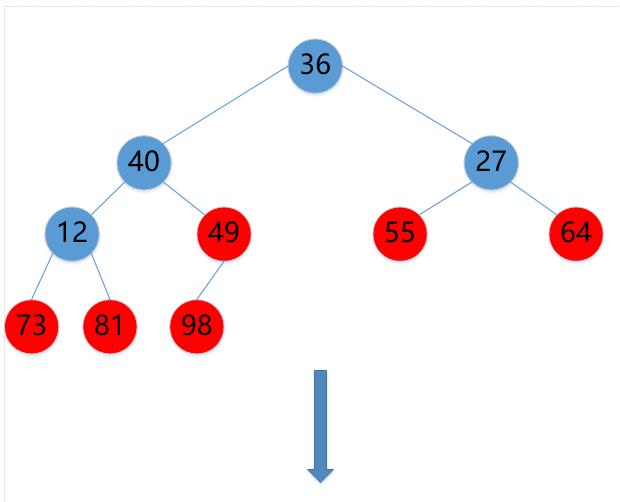
(12)36->40

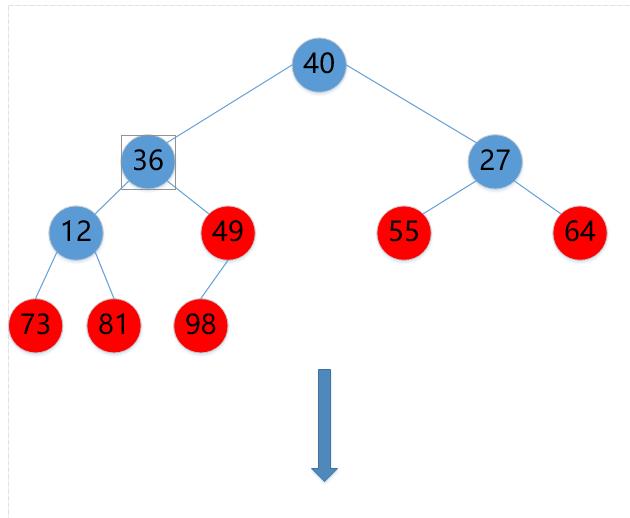
(13)40->12

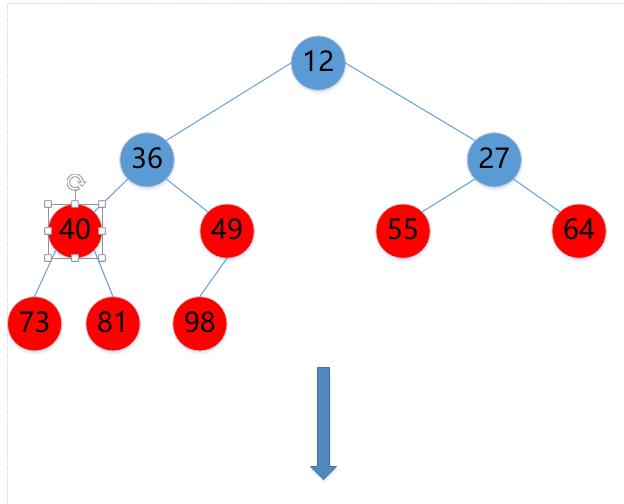
(14)12->36

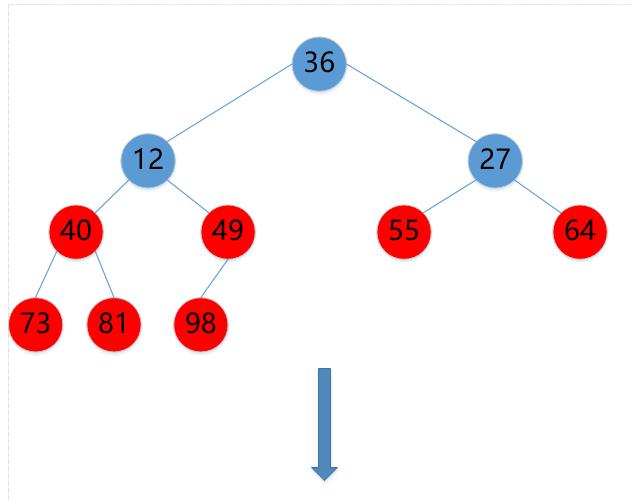
(15)36->27

 

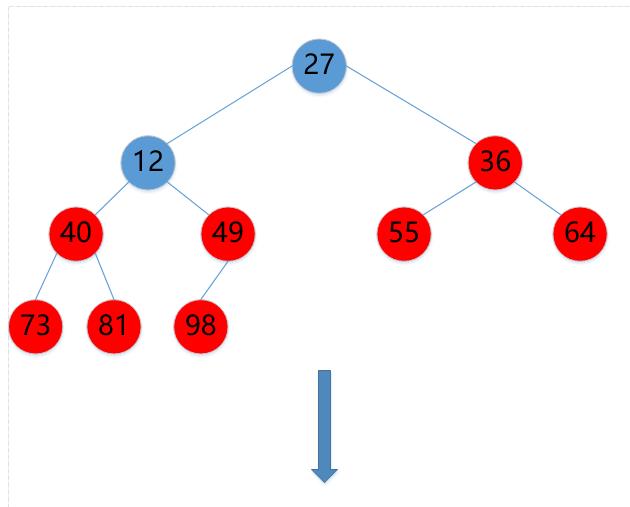
(16)27->12

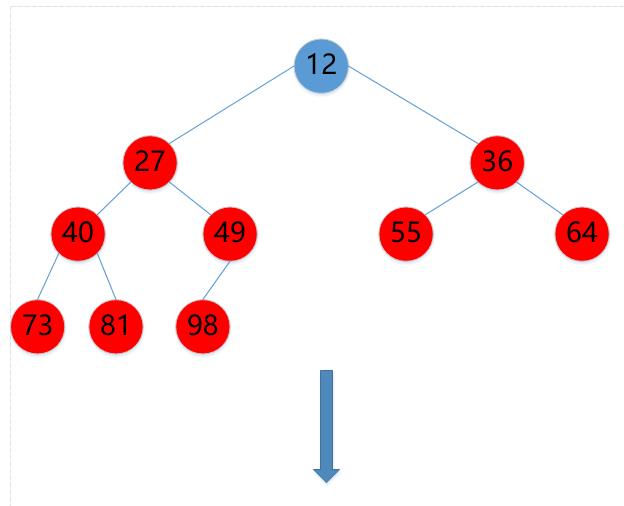
(16)12->12

 

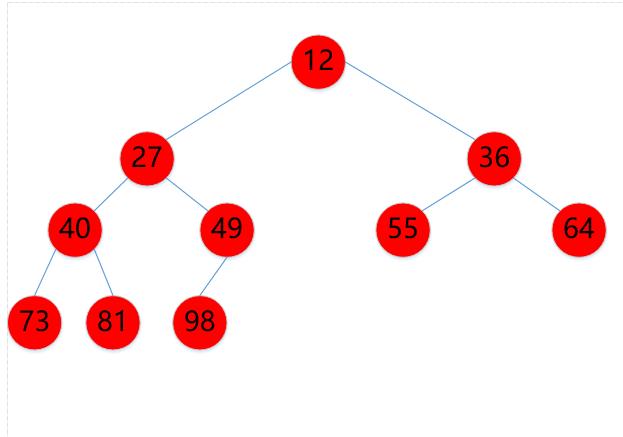
代码：

package com.zjl.tool.sort;

/**
 * 堆排序
 * @author huanongying
 *
 */
public class HeapSort {

    /**
     * @param args
     */
    public static void main(String[] args) {
        int[] arr = {40,55,49,73,12,27,98,81,64,36};//待排序数组
        HeapSort(arr, arr.length - 1);//将arr按照降序排列
        //打印排序后的数组
        for(int value : arr) {
            System.out.print(value + " ");
        }
    }

    /**
     * 待排序列（R1，R2，...，Rk,...Rn）看作是完全二叉树，通过比较、交换，父节点和孩子节点的值，
     * 使得对于任意元素Rk（k<=n/2）,满足Rk>=R(2k),Rk>=R(2k+1)
     * @param arr    数组对象
     * @param start    数组的开始下标
     * @param end    数组的结束下标
     */
    private static void HeapAdjust(int[] arr, int start, int end) {
        //当下标为start的元素有孩子元素时
        while(start <= end/2) {
            //left和right分别为左右孩子元素的下标,max为左右孩子中值较大的孩子的元素下标
            int left = 2 * start+1;
            int right = 2 * start+2;
            int max = 0;
            
            //如果既有左孩子，又有右孩子
            if(left < end&&right <= end) {
                //如果左孩子小于右孩子的值，max = right，否则为max = left
                if(arr[left] <= arr[right])
                    max = right;
                else
                    max = left;
            }
            //如果只有左孩子，没有右孩子，max值为left
            if(left <= end&&right > end) {
                max = left;
            }
            //如果没有孩子，则表明到了完全二叉树的叶子节点
            if(left > end) {
                break;
            }
            
            //如果当前节点值小于两孩子中的值较大者，那么将当前节点值与max交换
            if(arr[start] < arr[max]){
                int tmp = arr[start];
                arr[start] = arr[max];
                arr[max] = tmp;
            }
            //当前节点向孩子节点迭代
            start = max;
        }
    }

    /**
     * @param arr 数组
     * @param end    数组结束下标
     */
    private static void HeapSort(int[] arr, int end) {
        //由最后一个非叶子节点，向根节点迭代，创建最大堆，数组中的最大值将被移动到根节点
        for(int start = end/2;start >= 0;start--) {
            HeapAdjust(arr, start, end);
        }
        
        while(end > 0){
            //交换arr[0]和arr[end]的值
            int tmp = arr[0];
            arr[0] = arr[end];
            arr[end] = tmp;
            
            //排序范围变为(0,end-1)
            HeapAdjust(arr, 0, end - 1);
            end--;
        }
    }

}