四校联考比赛题解FJ NOIP 四校联考 2017 Round 7

Posted 2020-10-09 PinkRabbit

此次比赛为厦门一中出题。都是聚劳，不敢恭维。

莫名爆了个0，究其原因，竟然是快读炸了……很狗，很难受。

话不多说，来看看题：

【T1】

题意：

样例：

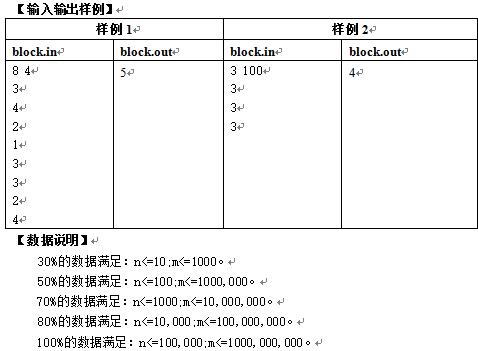
PS：1<=h[i]<=100000。

题解：

假设\\(max\\left(h_{i}\\right)=M\\)，可以发现最大高度不超过\\(M+n\\)。

而用\\(m\\)块砖，向上最多能搭\\(\\sqrt{m}\\)个。

故最大高度为\\(M+min\\left(n,\\sqrt{m}\\right)\\)。

而最低高度为\\(M\\)（或\\(M+1\\)）。

也就是说，高度的范围不超过3163。

而可以看出对于高度\\(h\\)，能否搭建起高\\(h\\)的塔是单调的。

如果我们二分高度\\(h\\)，计算能否搭建，就能够较快出解。

考虑在第\\(i\\)列搭上\\(h\\)的高度，那么最少需要多少砖块呢？

当然是按照金字塔形斜向下，直到遇到第一个可以作为支撑的砖块。

设\\(left\\left[i\\right]\\left[h\\right]\\)为坐标\\(\\left(i,h\\right)\\)向左斜向下遇到的第一个砖块的标号，\\(right\\left[i\\right]\\left[h\\right]\\)则为向右斜向下，若不存在，则值为0。

那么最少需要的砖块数（包括已经搭建的）等于：

\\(Sum[i][h]=h(right[i][h]-left[i][h]-1)-\\frac{(i-left[i][h])(i-left[i][h]-1)}{2}-\\frac{(right[i][h]-i)(right[i][h]-i-1)}{2}\\)。

而需要多搭的为：\\(Sum[i][h]-(sum_{right[i][h]-1}-sum_{left[i][h]})\\)，其中\\(sum\\)为前缀和。

现在，如何快速算出\\(left\\)和\\(right\\)呢？

看往左斜向下的，容易发现，\\(k\\)能够阻挡\\((i,h)\\)当且仅当\\(h_{k}-k\\geqslant h-i\\)。

而对于向右下方的，我们有，\\(k\\)能够阻挡\\((i,h)\\)当且仅当\\(h_{k}+k\\geqslant h+i\\)。

考虑记录下\\(L_{k}=h_{k}-k\\)与\\(R_{k}=h_{k}+k\\)。

那么我们就是对特定\\(i,h\\)要求出从右往左第一个\\(k\\)使得\\(L_{k}\\geqslant h-i\\)，求出从左往右第一个\\(k\\)使得\\(R_{k}\\geqslant h+i\\)。

这是单调栈的模型，先把\\(L_{k}\\)和\\(R_{k}\\)用单调栈维护一遍。

而在计算过程中，\\(h+i\\)与\\(h-i\\)是单调递增或递减的，这有了双指针扫描的可能性。

这就是整体思路，代码有点复杂……

 1 #include<cstdio>
 2 #define F(i,a,b) for(int i=a;i<=b;++i)
 3 #define dF(i,a,b) for(int i=a;i>=b;--i)
 4 int n,m,h[100005],Ans,M;
 5 long long sum[100005];
 6 int left[100005][2],lp,right[100005][2],rp;
 7 int L[100005],R[100005];
 8 inline int Max(int x,int y){return x>y?x:y;}
 9 void init(){
10     scanf("%d%d",&n,&m);
11     F(i,1,n) scanf("%d",h+i), M=Max(M,h[i]);
12     F(i,1,n) sum[i]=sum[i-1]+h[i];
13     lp=0;
14     F(i,1,n){
15         while(lp&&left[lp][0]<=h[i]-i) --lp;
16         left[++lp][0]=h[i]-i;
17         left[lp][1]=i;
18     } left[0][0]=99999999;
19     rp=0;
20     dF(i,n,1){
21         while(rp&&right[rp][0]<=h[i]+i) --rp;
22         right[++rp][0]=h[i]+i;
23         right[rp][1]=i;
24     } right[0][0]=99999999;
25 //    F(i,1,lp) printf("(%d,%d) ",left[i][0],left[i][1]); puts("");
26 //    F(i,1,rp) printf("(%d,%d) ",right[i][0],right[i][1]); puts("");
27     Ans=M;
28 }
29 int main(){
30     freopen("block.in","r",stdin);
31     freopen("block.out","w",stdout);
32     init();
33     int l=M+1, r=M+40000, mid, ok;
34     while(l<=r){
35         mid=(l+r)>>1;
36         ok=0;
37 //        printf("%d:\\n",mid);
38         for(int i=1,pos=1;i<=n;++i){
39             L[i]=0;
40             if(pos!=lp&&left[pos+1][0]>=mid-i) ++pos;
41             if(left[pos][0]>=mid-i) L[i]=left[pos][1]+1;
42         }
43 //        for(int i=1;i<=n;++i) printf("%d ",L[i]); puts("");
44         for(int i=n,pos=1;i>=1;--i){
45             R[i]=0;
46             if(pos&&right[pos+1][0]>=mid+i) ++pos;
47             if(right[pos][0]>=mid+i) R[i]=right[pos][1]-1;
48         }
49 //        for(int i=1;i<=n;++i) printf("%d ",R[i]); puts("");
50         F(i,1,n){
51             if(L[i]==0||R[i]==0) continue;
52             long long Sum=
53             (long long)mid*(R[i]-L[i]+1)-
54             (long long)(i-L[i]+1)*(i-L[i])/2-
55             (long long)(R[i]-i+1)*(R[i]-i)/2-
56             (sum[R[i]]-sum[L[i]-1]);
57 //            printf("%d:%lld ",i,Sum);
58             if(Sum<=m) {ok=1; break;}
59         }//puts("");
60         if(ok) l=mid+1, Ans=mid;
61         else r=mid-1;
62     }
63     printf("%d",Ans);
64     return 0;
65 }

【T2】

题意：

样例：

题解：

 1 #include <cstdio>
 2 #include <cstring>
 3 #include <algorithm>
 4 #include <cassert>
 5 using namespace std;
 6 #define rep(i,a,n) for (int i=a;i<n;i++)
 7 #define per(i,a,n) for (int i=n-1;i>=a;i--)
 8 typedef long long ll;
 9 // head
10 
11 const int N=2501000;
12 int n,m,cnt0[N],cnt1[N];
13 ll m0,md,cnt2[N];
14 int main() {
15     freopen("cake.in","r",stdin);
16     freopen("cake.out","w",stdout);
17     scanf("%d%d",&m,&n);
18     scanf("%lld%lld",&m0,&md);
19     rep(i,1,m+1) {
20 //        printf("%lld\\n",m0);
21         cnt0[m0]++;
22         m0=(m0*58+md)%(n+1);
23     }
24 //    puts("");
25     scanf("%lld%lld",&m0,&md);
26     rep(i,1,n+1) {
27 //        printf("%lld\\n",m0);
28         cnt1[m0]++; cnt2[m0]+=m0;
29         m0=(m0*58+md)%(m+1);
30     }
31     int x=0; ll sx=0;
32     rep(i,1,m+1) cnt1[i]+=cnt1[i-1],cnt2[i]+=cnt2[i-1];
33     ll ans=cnt2[m];
34 //    puts("");
35     rep(i,0,n+1) {
36         rep(j,0,cnt0[i]) {
37             x++; sx+=i;
38             int y=cnt1[m-x];
39             assert(x<=m&&y<=n);
40             ll ret=(ll)(m-x)*(n-y)+cnt2[m-x]+sx;
41 //            printf("%lld\\n",ret);
42             ans=min(ans,ret);
43         }
44     }
45     printf("%lld\\n",ans);
46 }

【T3】

题意：

题解：

我个人不会做……有待学习。

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<algorithm>
  4 #include<vector>
  5 #define rep(i,a,b) for(int i=(a);i<=(b);i++)
  6 #define per(i,a,b) for(int i=(a);i>=(b);i--)
  7 #define Rep(i,x) for(int i=head[x];i+1;i=nxt[i])
  8 #define pb push_back
  9 #include<algorithm>
 10 using namespace std;
 11 typedef long long ll;
 12 const int N=4e6+5;
 13 const int M=8e6+5;
 14 inline void read(int &x){x=0;char ch=getchar(); while(ch<\'0\') ch=getchar(); while(ch>=\'0\'){x=x*10+ch-48;ch=getchar();}}
 15 inline void judge()
 16 {
 17     freopen("tree.in","r",stdin);
 18     freopen("tree.out","w",stdout);
 19 }
 20 int fa[N],head[N],nxt[M],to[M],e,w[M],id[M];
 21 int wod[N];
 22 int son[N][2],pd[N],tp[N];
 23 inline void init(){memset(head,-1,sizeof(head)); e=0;}
 24 inline void add_edge(int x,int y,int z,int ii){to[e]=y;w[e]=z;nxt[e]=head[x];id[e]=ii;head[x]=e++;}
 25 ll ma[N][2],ans[N][2];
 26 inline void Insert(int x,ll y,int cjl,int ii)
 27 {
 28     if(ma[x][0]<y){ma[x][1]=ma[x][0];ma[x][0]=y;son[x][1]=son[x][0];son[x][0]=cjl;pd[x]=ii;}
 29     else if(y>ma[x][1]){ma[x][1]=y;son[x][1]=cjl;}
 30 }
 31 void dfs(int x)
 32 {
 33     ma[x][0]=ma[x][1]=0;Rep(i,x)
 34     {
 35         int j=to[i]; if(j==fa[x]) continue; fa[j]=x; tp[j]=id[i];
 36         dfs(j); Insert(x,ma[j][0]+(ll)w[i],j,tp[j]);
 37     }
 38 }
 39 inline void Insert3(int x,ll y)
 40 {
 41     if(ma[x][0]<y){ma[x][1]=ma[x][0];ma[x][0]=y;}
 42     else if(y>ma[x][1])ma[x][1]=y;
 43 }
 44 void dfs3(int x,int f,int pp)
 45 {
 46     ma[x][0]=ma[x][1]=0;ans[pp][0]=0;Rep(i,x)
 47     {
 48         int j=to[i]; if(j==f) continue;
 49         dfs3(j,x,id[i]); Insert3(x,ma[j][0]+(ll)w[i]);
 50         ans[pp][0]=max(ans[pp][0],ans[id[i]][0]);
 51     }ans[pp][0]=max(ans[pp][0],ma[x][0]+ma[x][1]);
 52 }
 53 vector<int> tt,Route,Rid,tt2;
 54 void dfs2(int x)
 55 {
 56     tt.push_back(x); if(pd[x])tt2.push_back(pd[x]);
 57     if(son[x][0]) dfs2(son[x][0]);
 58     else return;
 59 }
 60 ll md[N];
 61 int main()
 62 {
 63     judge();
 64     int n;read(n);init();rep(i,1,n-1)
 65     {
 66         int x,y,z;read(x);read(y);read(z);
 67         add_edge(x,y,z,i);add_edge(y,x,z,i);
 68         wod[i]=z;
 69     }fa[1]=0;dfs(1);int mj=1;rep(i,2,n) if(ma[i][0]+ma[i][1]>ma[mj][0]+ma[mj][1]) mj=i;
 70     rep(i,1,n-1) ans[i][1]=ma[mj][0]+ma[mj][1];
 71     if(son[mj][0])
 72     {
 73         dfs2(son[mj][0]); for(int i=(int)tt.size()-1;i>=0;i--) Route.pb(tt[i]);
 74         for(int i=(int)tt2.size()-1;i>=0;i--) Rid.pb(tt2[i]); tt2.clear();tt.clear();
 75         Rid.pb(tp[son[mj][0]]);
 76     }
 77     Route.pb(mj);
 78     if(son[mj][1])
 79     {
 80         Rid.pb(tp[son[mj][1]]);
 81         dfs2(son[mj][1]); for(int i=0;i<(int)tt.size();i++) Route.pb(tt[i]);
 82         for(int i=0;i<(int)tt2.size();i++) Rid.pb(tt2[i]);
 83     }
 84     int sz=Route.size();memset(ma,0,sizeof(ma));
 85     ll pre=0;ll maa=0;
 86     rep(i,0,sz-1)
 87     {
 88         int j=Route[i];
 89         Rep(xjt,j)
 90         {
 91             if(i && to[xjt]==Route[i-1]) continue;
 92             if(i<sz-1 && to[xjt]==Route[i+1]) continue;
 93             dfs3(to[xjt],j,id[xjt]); md[i]=max(md[i],w[xjt]+ma[to[xjt]][0]);
 94         }
 95         maa=max(maa,md[i]+pre);if(i!=sz-1)ans[Rid[i]][0]=maa;
 96         if(i!=sz-1) pre+=wod[Rid[i]];
 97     }
 98     pre=0; maa=0;memset(md,0,sizeof(md));
 99     per(i,sz-1,0)
100     {
101         int j=Route[i];
102         Rep(xjt,j)
103         {
104             if(i && to[xjt]==Route[i-1]) continue;
105             if(i<sz-1 && to[xjt]==Route[i+1]) continue;
106             dfs3(to[xjt],j,id[xjt]); md[i]=max(md[i],w[xjt]+ma[to[xjt]][0]);
107         }
108         maa=max(maa,md[i]+pre);if(i)ans[Rid[i-1]][1]=maa;
109         if(i) pre+=wod[Rid[i-1]];
110     }
111     rep(i,1,n-1) if(ans[i][0]>ans[i][1]) swap(ans[i][0],ans[i][1]);
112     ll solo=0;
113     rep(i,1,n-1)
114     {
115         solo+=ans[i][1]*23333ll+ans[i][0]*2333ll+233ll*(ll)i*(ll)i+23ll*(ll)i+2ll;
116         //cerr<<ans[i][1]<<\' \'<<ans[i][0]<<endl; 
117         solo%=2333333333333333ll;
118     }
119     printf("%lld\\n",solo);
120     return 0;
121 }