序列模式

Posted 2020-10-09 懵懂的菜鸟

序列模式

1 序列模式

在Web数据挖掘中，从用户浏览网页的顺序中挖掘网站的浏览模式是很有用的；在文本挖掘中，根据词在句子中的顺序挖掘语言模式也是非常重要的。对于这些应用，序列模式挖掘发挥着重要的作用。序列模式挖掘即从序列数据库中发现频繁子序列以作为模式,它是一类重要的数据挖掘问题,有着非常广泛的应用前景,被应用在包括顾客购买行为的分析、网络访问模式分析、科学实验的分析、疾病治疗的早期诊断、自然灾害的预测、DNA 序列的破译等方面。

序列模式挖掘问题的定义：

一个序列中项集的个数称为该序列的基数。

一个序列中项目中的个数称为该序列的长度。长度为k的序列称为k-序列。如果某个项目在一个序列的多个元素中出现，其每次出现都累加到k上。

序列模式可以简单的理解为关联规则+时间维度。

序列模式挖掘问题是找出所有满足用户指定的最小支持度的序列。

一个序列的支持度是指序列数据库中有该序列的数据占总数据的比重。

序列挖掘算法的步骤：1、排序阶段；2、频繁项集阶段；3、转换阶段；4、序列阶段利用已知的频繁集的集合来找出所需的序列。

常见的序列挖掘算法有AprioriAll算法、AprioriSome算法、GSP算法、MS-GSP算法和PrefixSpan算法。

1. AprioriAll算法和Apriori算法唯一的不同是在合并时，需要区分最后两个元素的顺序。

   AprioriAll算法^[1]

   输入：大项集阶段转换后的序列数据库

   输出：所有最长序列

   1) L1={large1- sequence};//大项集阶段得到的结果

   2) For(k=2;Lk-1≠0;k++)do begin

   3) Ck=Candidate-generate(Lk-1)//Ck是从Lk-1中产生的新的候选者

   4) For each customer-sequence c in the database do//对数据库中的每一个顾客序列c

   5) Increment the count of all candidates in Ck that are contained in c;//对包含于c中Ck内的所有候选者计数

   6) Lk=Candidates in Ck with minimumsuport;//Lk为Ck中满足最小支持度的候选者

   7) End

   8) Answer=Maximal Sequences in ∪kLk

   其中候选集生成算法Ck=Candidate-generate(Lk-1)如下：

   输入：所有的大(k-1)序列的集合

   输出：候选 Ck

   1) Insert into Ck//首先进行 Lk-1与Lk-1的连接运算

   select p.litemset1,…,p.litemseti-1,q.litemseti-1

   from LK-1 p,Lk-1 q//p和q是Lk-1 中两个不同的序列串

   where p.litemset1=q.litemset1,…,

   p.litemsetk-2=q.litemsetk-2;

   2) delete all sequences c ∈Ck such that some//对候选者进行修剪(修剪的理论是频繁模式集的子集合也是频繁的)

    

2. AprioriSome算法是Apriori算法的改进，具体过程分为两个阶段：
3. 前推阶段：此阶段用于找出指定长度的所有大序列
4. 回溯阶段：此阶段用于查找其他长度的所有大序列

   AprioriSome算法

   输入：大项集阶段转换后的序列数据库DT

   输出：所有最长序列

   // Forward Phase — 前推阶段；

   1） L1 = {large 1-sequences};//大项目集阶段的结果；

   2） C1 = L1;

   3） last = 1;//最后计数的Clast

   4） FOR(k =2;Ck-1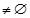and Llast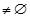;k++)DO BEGIN

   5） IF (Lk-1 know)THEN Ck = New candidates generated from Lk-1;//Ck＝产生于Lk-1新的候选集

   6） ELSE Ck = New candidates generated from Ck-1;// Ck＝产生于Ck-1新的候选集

   7） IF (k =next(last)) THEN BEGIN

   8） FOR each customer-sequence c in the database DO//对于在数据库中的每一个客户序列c

   9） Sum the count of all candidates in Ck that are contained in c;

   //求包含在c中的Ck的候选者的数目之和

   10） Lk = Candidates in Ck with minimum support;// Lk＝在Ck中满足最小支持度的候选者

   11） last = k;

   12） END;

   13）END;

   // Backward Phase — 回溯阶段；

   14）FOR (k - - ;k > = 1;k - - ) DO

   15）IF (Lk not found in forward phase) THEN BEGIN// Lk在前推阶段没有确定的情况

   16） Delete all sequences in Ck contained in Some Li, i > k;//删除所有在Ck中包含在Lk中的序列，i>k

   17） FOR each customer-sequence c in DT DO//对于在DT中的每一个客户序列c

   18） Sum the count of all candidates in Ck that are contained in c;//对在Ck中包含在c中的所有的候选这的计数

   19） Lk = Candidates in Ck with minimum support// Lk =在Ck中满足最小支持度的候选者

   20）END;

   21）ELSE Delete all sequences in Lk contained in Some Li,i > k;// Lk 已知

   22）Answer = ∪k Lk; //从k到m求Lk的并集

   在前推阶段（forward phase）中，我们只对特定长度的序列进行计数。比如，前推阶段我们对长度为1、2、4和6的序列计数（计算支持度），而长度为3和5的序列则在回溯阶段中计数。next函数以上次遍历的序列长度作为输入，返回下次遍历中需要计数的序列长度。

   其中next()算法如下：

   next（k: integer）

   1） IF （hitk < 0.666）THEN return k + 1；

   2） ELSEIF （hit k < 0.75）THEN return k + 2；

   3） ELSEIF （hit k < 0.80）THEN return k + 3；

   4） ELSEIF （hit k < 0.85）THEN return k + 4；

   5） ELSE THEN return k + 5；

   hitk被定义为大k-序列（large k-sequence）和候选k-序列（candidate k-sequence）的比率，即|Lk|/|Ck|。这个函数的功能是确定对哪些序列进行计数，在对非最大序列计数时间的浪费和计算扩展小候选序列之间作出权衡。

   （3）AprioriAll和AprioriSome算法比较：

   1） AprioriAll用Lk-1去算出所有的候选Ck，而AprioriSome会直接用Ck-1去算出所有的候选 Ck.，因为Ck-1包含Lk-1，所以AprioriSome会产生比较多的候选。

   2）虽然AprioriSome跳跃式计算候选，但因为它所产生的候选比较多，可能在回溯阶段前就占满内存。

   3）如果内存满了，AprioriSome就会被强迫去计算最后一组的候选，（即使原本是要跳过此项）。这样，会影响并减少已算好的两个候选间的跳跃距离，而使得AprioriSome会变的跟AprioriAll一样。

   4）对于较低的支持度，有较长的大序列，也因此有较多的非最大序列，所以AprioriSome比较好。

   （4）GSP算法

   GSP算法的基本思想和Apriori算法一样，其主要步骤包括三个步骤：

   1）扫描序列数据库，得到长度为1的序列模式L1，作为初始的种子集；

   2）根据长度为i的种子集Li通过连接操作和剪切操作生成长度为i+1的候选序列模式Ci+1；然后扫描序列数据库，计算每个候选序列模式的支持数，产生长度为i+1的序列模式Li+1，并将Li+1作为新的种子集；

   3）重复第二步，直到没有新的序列模式或新的候选序列模式产生为止。

   其中，产生候选序列模式主要分两步：

   连接阶段：如果去掉序列模式S1的第一个项目与去掉序列模式S2的最后一个项目所得到的序列相同，则可以将S1于S2进行连接，即将S2的最后一个项目添加到S1中。

   剪切阶段：若某候选序列模式的某个子序列不是序列模式，则此候选序列模式不可能是序列模式，将它从候选序列模式中删除。

   GSP算法

   输入：大项集阶段转换后的序列数据库DT。

   输出：最大序列

   1） L1 = {large 1-sequences};// 大项集阶段得到的结果

   2） FOR (k = 2;Lk-1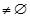;k++) DO BEGIN

   3） Ck = GSPgenerate(Lk-1);//序列模式挖据

   4） FOR each customer-sequence c in the database DT DO

   5） Increment the count of all candidates in Ck that are contained in c;

   6） Lk = Candidates in Ck with minimum support;

   7） END;

   8） Answer = Maximal Sequences in ∪kLk;

   （4）MS-GSP算法

   MS-GSP算法是基于逐级搜索的。第1行将项目的MIS值升序排序，保存在MS中。第2行运行init-pass()函数进行第一轮搜索，和MS-Apriori算法中的功能一样，返回种子集合L，用于生成长度为2的候选序列集合C2。

   

   在接下来的每一轮搜索中，算法的工作机理和MS-Apriori算法相似。evel2-candidate-gen函数可以基于MS-Apriori算法中的Level2-candidate-gen函数和GSP模式中的合并操作给出。c.minMISItem表示在候选序列c中具有最低的MIS值的项目。在序列挖掘模式中，具有最小MIS值的项目可以位于序列的任意位置。算法的13-14行用来确保所有的序列规则在MS-GSP算法运行完成之后可以直接生成而不需要再扫描数据。

   对于序列模式挖掘，项目的顺序是很重要的，这就使得合并操作比较麻烦。其中MScandidate-gen-SPM函数相对比较复杂，其算法过程如下：

   Funcation MScandidate-gen-SPM(Fk-1)

5. 合并生成候选序列时。
6. 如果S1的第一个项目的MIS值要比S1中其他每个项目的MIS值小，然后如果满足：

   1）将S1的第二个项目和S2的最后一个项目删除之后得到的两个子序列是相同的。

   2）S2的最后一个项目的MIS值要比S1的第一个项目的MIS值大，则序列S1和S2合并。将S2的最后一个项目扩展到S1尾部生成候选序列：

   如果S2的最后一个项目{l}是独立的元素，那么将{l}以一个单独元素的形式扩展到S1末尾，生成候选序列C1。

   如果（S1的长度和基数都是2）并且（S2的最后一个项目要比S1的最后一个项目大）

   那么保持{l}加入到S1最后的元素的末尾生成候选序列C2。

   如果（（S1的长度为2，基数为1）并且（S2最后一个项目要比S1最后一个项目大））或者（S1的长度大于2）

   那么S2最后一个元素加入到S1最后元素的末尾生成候选序列C2。

   （3）否则，如果S2最后一个项目的最后一个项目MIS值要比S2中其他项目都小，那么上述方法反过来用。

   （4）否则，采用GSP中的合并方法

   （5）剪枝。在一个k候选序列的所有（k-1）-子序列中，如果除了唯一的不包含具有最小MIS值的项目的子序列之外，其他子序列都是非频繁的，则这个候选序列将被剪枝。

   （5）PrefixSpan算法

   GSP算法可以视为采用广度优先搜索查找所有的序列模式，而PrefixSpan则采用深度优先搜索。PrefixSpan算法在算法的过程中不产生候选集，给定初始前缀模式，不断的通过后缀模式中的元素转到前缀模式中，而不断的递归挖掘下去。其算法如下^[2] ：

   PrefixSpan(α,l, b)

   参数:

   α指前缀序列模式;

   l指α的长度;

   b指α的投影数据库;

   算法：

   （1）扫描，找出频繁项集b：
           1）b可以成为α的最后一个项集（如ab + c=> abc），或者:
           2）b可以追加到α形成新一个序列模式（如ab +_c => a(bc)）;

   （2）对于每个频繁项b，追加到α形成新一个序列模式α\'（如abc或a(bc)）;

   （3）对于每个α\'，构造α\'的投影数据库，并调用prefixspan(α\', l+1, b);

   其过程为深度优先搜索。

   投影数据库，是序列数据库S中所有相对于α前缀的后缀序列的集合。L例如：

   对于序列<a(abc)(ac)d(cf)>，

   <(abc)(ac)d(cf)>是前缀<a>的后缀；

   <(_bc)(ac)d(cf)>是前缀<aa>的后缀；

   <(_c)(ac)d(cf)>是前缀<a(ab)>的后缀；

   "_"下标符代表前缀。

   2 从序列模式中产生规则

   至今序列模式的挖掘还没有定义生成，但事实上定义几类规则并进行数据挖掘也是可行的。例如定义标签序列规则（Label Sequential Rules）。

   一个标签序列规则是形如X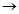Y的蕴含关系，其中Y是一个序列，X是一个将Y中的一些项目替换成通配符而得到的序列。一个通配符用*表示，可以匹配任何项目。被替换掉的项目一般称为标签。所有标签形成数据集中一个很小的项目集合。

   

   例如：从表2.6中可以找到一个序列数据库，设最小支持度为30%，最小置信度为60%，可以找到一个标签序列规则

   <{1}{*}{7,*}>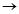<{1}{3}{7,8}>

   标签规则序列在一些实际应用中还是有用的，例如需要预测一个输入序列中的标签项目，例如上例中的3和8。规则的置信度是包含<{1}{*}{7,*}>的序列中两个通配符分*别为3和8的概率估计。例如，在LSR的例子中，想要预测一个比较性的句子中某一个单词是否是一个实体，而这里把实体建模为标签。

    

    

    

    

    

    

   参考文献：

   [1] http://wenku.baidu.com/view/19ee9abd960590c69ec376c6.html

   [2] http://blog.csdn.net/textboy/article/details/52526239

    

   附录：AprioriAll算法实例

   表一

   交易发生的时间	客户标识	购买项
   June 10\'04	2	A，B
   June 12\'04	5	H
   June 15\'04	2	C
   June 20\'04	2	D，F，G
   June 25\'04	4	C
   June 25\'04	4	C，E，G
   June 25\'04	1	C
   June 30\'04	1	H
   June 30\'04	4	D，G
   July 25\'04	4	H

    

   重新排序阶段

   表二

   客户标识	交易时间	购买项
   1	June 25\'04	C
   1	June 30\'04	H
   2	June 10\'04	A,B
   2	June 15\'04	C
   2	June 20\'04	D,F,G
   3	June 25\'04	C,E,G
   4	June 25\'04	C
   4	June 30\'04	D,G
   4	July 25\'04	H
   5	June 12\'04	H

    

   由客户标识及交易发生的时间为关键字所排序的数据库

   表三

   客户号	客户序列
   1	< (C) (H) >
   2	< (A,B) (C) (D,F,G) >
   3	< (C,E,G) >
   4	< (C) (D,G) (H) >
   5	< (C) (D,G) (H) >

    

    

   客户序列描述数据库

   表四

   频繁项集	映射
   (C)	1
   (D)	2
   (G)	3
   (DG)	4
   (H)	5

    

   频繁项集分别是(C)、(D)、(G)、(D,G)和(H)

    

   转换阶段：

   表五

   客户标识	原始客户序列	转换后客户序列	映射后序列
   1	<(C)(H)>	<{(C)}{(H)}>	<{1}{5}>
   2	<(A,B)(C)(D,F,G>	<{(C)}{(D)(G),(D,G)}>	<{1}{2,3,4}>
   3	<(C,E,G)>	<{(C),(G)}>	<{1,3}>
   4	<(C)(D,G)(H)><(H>	<{(C)}{(D),(G),(D,G)}{(H>	<{1}{2,3,4}{5}>
   5		<{(H)}>	<{5}>

    

   序列阶段：

   表六

   客户号	客户序列
   1	<{1 5}{2}{3}{4}>
   2	<{1}{3}{4}{3 5}>
   3	<{1}{2}{3}{4}>
   4	<{1}{3}{5}>
   5	<{4}{5}>

    

   本例子我们设定的Min-support=2，其求解过程如下表。

   表七 L₁：

   1-序列	支持度
   <1>	4
   <2>	2
   <3>	4
   <4>	4
   <5>	4

    

    

   L₂：表八

   2-序列	支持度
   <1 2>	2
   <1 3>	4
   <1 4>	3
   <1 5>	3
   <2 3>	2
   <2 4>	2
   <3 4>	3
   <3 5>	2
   <4 5>	2

    

    

    

    

   L₃：表九

   3-序列	支持度
   <1 2 3>	2
   <1 2 4>	2
   <1 3 4>	3
   <1 3 5>	2
   <2 3 4>	2

    

   L₄：表十

   4-序列	支持度
   <1 2 3 4>	2

    

   最大频繁子序列：表十

   序列	支持度
   〈1 2 3 4〉	2
   〈1 3 5〉	2
   〈4 5〉	2