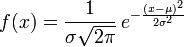入门基础知识

Posted 2020-10-09 Aaron12

数据分析入门

　　大数据的流程：数据收集、数据储存、数据建模、数据分析、数据变现。

　　

　　大量看似不相关的事却能够通过观察分析告诉人们背后的因果，并预测未来趋势。

　　数据：承载了信息的东西才是数据

　　信息：把我们不清楚的事情阐明的描述

排列组合与古典概型

　　古典概型：包含的单位事件是有限的，且单位事件包含的概率相等（例如抛硬币）

　　排列组合：从某些数据中驱逐一部分，有先后顺序的组合（例如买彩票，不同数字的组合）

统计与分布

　　理解几个名词：加权值、平均值、标准差、众数、中位数、抽样

　　标准差：（偏离平均值的程度，波动程度）

　　公式：

• 

　　欧氏距离：用于描述多维点之间的距离

　　二维：

　　三维：

　　N维：

　　曼哈顿距离：两个点在标准坐标系上的绝对轴距总和

　　

　　又称为出租车距离，例如在横平竖直的街道，出租车从一个位置到另外一个位置的距离。曼哈顿距离更多的是应用意义。

　　同比与环比：

　　同比：与相邻时段的同一时期相比

　　环比：直接和报告的上一时期相比

　　高斯分布：又成为正态分布，知道概率密度函数

　　若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布，记为：

X∼N(μ,σ2),

　　则其概率密度函数为

正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度

 

 

泊松分布：常见的离散概率分布，参数λ表示单位时间内发生某件事的概率。泊松分布适合描述单位时间内随机事件发生的次数，

 

伯努利分布：需要满足以下两个条件

（1）：每次实验的结果是相互独立的，男和你的概率为p和q

（2）：每次实验都只有两种结果，n=1或n=0

n重伯努利试验服从二项分布

满足公式：

 信息论：信息量的理解、香农公式、熵的理解、信息熵的计算

　　信息熵：对信息杂乱程度的量化描述

　　一个离散型随机变量 的熵 定义为：

　　

　　即若干个x产生的概率乘以该可能性产生的信息量，之后求和。

　　其中是信息量的计算公式

　　同一个问题中信息熵采用同一个底（对数底用2和10都可以）

　　信息熵的大小判断：信息越确定、越单一，信息熵越小

　　　　　　　　　　   信息越不确定、越混乱，信息熵越大

　　后面要介绍的判定树算法要利用信息熵进行条件的优化

多维向量空间

　　冗余在IT领域指同样的数据存储超过一份的情况

　　冗余的问题是：如果其中一个数据发生变化，另外一个相关数据也会发生变化，否则会出现信息矛盾

　　维度、向量、矩阵