求数组插值——复杂度为O(n)的快速算法

Posted 2020-10-08 16061163

一、问题描述

令A[1...n]是一个由n个数组成的数组，定义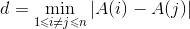为数组A的插值，其中|a|

表示a的绝对值。设计一个求数组插值的算法（用伪码描述）并分析算法的时间复杂度。

二、解决方案

核心思想：

将求数组差值问题转换为熟知的求数组最大连续子序列和问题。

实现过程：

数组A有n个元素如下：[A0,A1,A2,A3,...,An]，我们不妨先做一次转换，即创建新的数组B，B中有n-1个元素，分别是：

B0=A0-A1；

B1=A1-A2;

B2=A2-A3;

······

Bn-1=An-1-An-2;

假设数组A的差值为|Ai-Aj|，那么，对应的，|Ai-Aj|=|Bi + Bi+1 +...+ Bj-1|，显然，求数组A的差值问题就被我们转换成了求数组B的最大连续子序列和的绝对值的问题。

而通过动态规划，我们能够实现算法复杂度为O(n)。

过程伪码（JAVA代码）：

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		ArrayList<Integer> A = new ArrayList<Integer>(Arrays.asList(A1,A2,···,An));
		ArrayList<Integer> B = new ArrayList<Integer>();                //创建数组
		for (int i = 0 ; i < A.size()-1 ; i++){
			B.add(A.get(i) - A.get(i+1));
		}                                                                                        //向数组B中添加元素Ai-Ai+1
		//动态规划实现过程
		int maxhere,maxsum;
		maxhere=maxsum=B.get(0);
		for (int i = 1 ; i < B.size() ; i++){
			if (Math.abs(maxhere+B.get(i)) < Math.abs(B.get(i))){
				maxhere = B.get(i);
			}                                                                                    /*如果前面位置到A[i]的最大子序列和
			绝对值反而比|A[i]|要小，则以当前位置i结尾的最大子序列和为A[i]*/
			else{
				maxhere += B.get(i);
			}                                                                                   /*如果前面位置到A[i]的最大子序列和
			绝对值要比之前位置的更大，则取最大子序列和绝对值为两者之和*/
			if (Math.abs(maxhere) > Math.abs(maxsum)){
				maxsum = maxhere;
			}                                                                                     //更新最大子序列和的绝对值
		}
		System.out.println(Math.abs(maxsum));
	}

算法复杂度分析：

创建数组B的算法复杂度为O(n-1)，实现最大子序列和绝对值的算法复杂度为O(n-1)，则总体算法复杂度为O(n-1)+O(n-1)=O(n)，属于比较快速的算法。

|萌新想法，如有疏漏，望请大佬指正！