最大网络流——增广路算法

Posted 2020-10-08 Dijkstra_Liu

 

几句废话：
读了刘汝佳的书之后，感觉一切都是那么茫然，于是自己在网上找教程，自己一点点码的，大概用了三天。
网络流基础：
看来我很有必要说一下网络流的基础
网络流问题就是给你一个图，每个图的边权叫做这条边的流量，问你从起始点出发，有多少值能通过这些边流到重点
我知道你没看懂，举个例子：

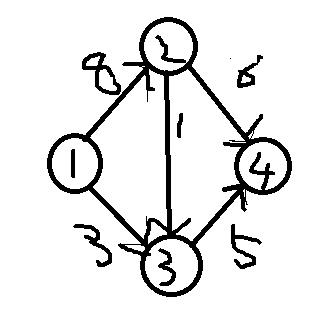
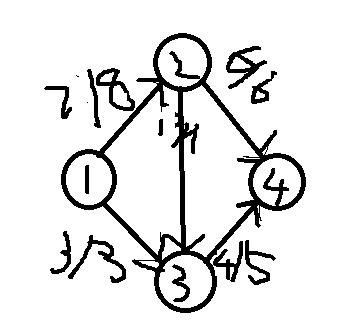
如图：

最大值为

从1到2到4运6个

从1到2到3到4运1个

从1到3到4运3个

一共运10个。

举例说完了，那么我说几个定义：

容量，就只一条边的权值，表示能从这条边运送的最大值

流量，表示一条边实际上流过的最大值

那么，说算法的时间到了，还是先上数据

（数据为上图所示）

4 5//四个点，五条边
1 2 8
1 3 3
2 3 1
2 4 6
3 4 5

开始，我们假设所有边的流量都是0

以这个数据，这样可以达到。

于是我们试图增加一些变得流量，使得重点的流量更大。

那么如何增加？就需要我们找増广路。

什么是増广路，就是一条从起点，到终点的一条每条边容量-实际流量>的路0。

比如

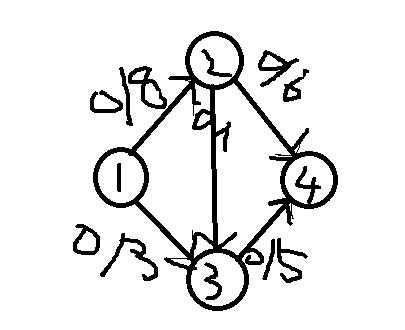
0/8表示一条边流量为0，容量为8

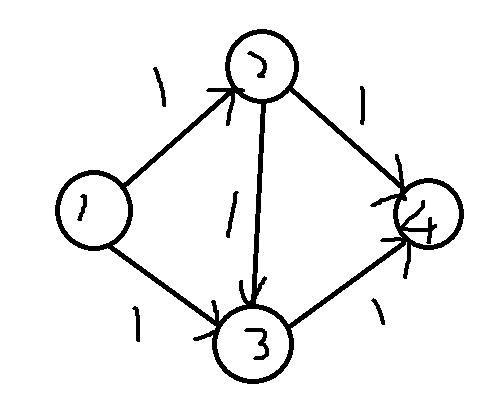
现在很明显可以看出，存在一条増广路1——2——4

然后怎么办，把这条路上的每条边流量都加上每条边容量与流量差的最小值

例如8-0>6-0 因此1——2、2——4这两条边的流量都加上6，并且答案也加上6

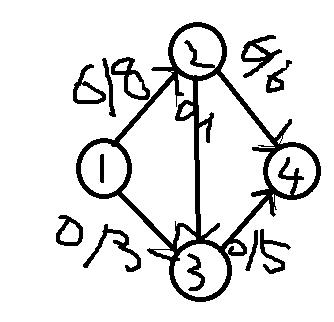
然后我们继续找増广路，又发现一条1——2——3——4

还是按刚才的，找出最小值，为1，所以这条增光路上每一边流量加1

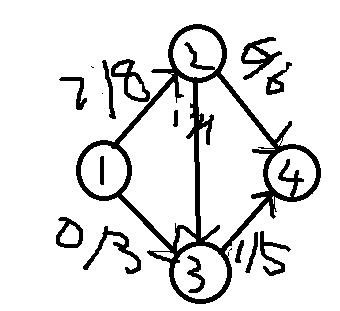
然后ans再加一变成7

然而我们继续找増广路，发现1——3——4

按照刚才，流量加上2，变成

ans加上3变成10

然后发现没有増广路了，于是算法结束，答案是10.

等等，这就要上代码了？传说中得noi算法网络流就这么简单？不存在的

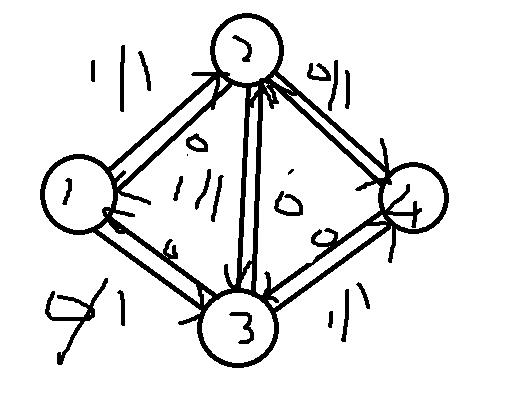
细心的同学（滑稽）会发现，这种情况就很神奇

你可能回算1——2——3——4这条増广路，于是答案是1，但是事实证明最优答案明显是2，那么问题出在哪里？

因为我们没有给予返回的机会，也就是相当于第一次找到的不是最优解，那么怎么办？

所以，我们要有一个反向边，来给程序反悔的机会，每条边都创建一条反向边，反向边的初始容量是0，流量都为负数。

假设1——2这条边本来权值是1，流量也是1，那么他的反向边的容量是0，流量是-1，这个应该好理解。

上图就会变为下图：

 

然后以刚才举例，当确定増广路1——2——3——4后，图是这样的：

 

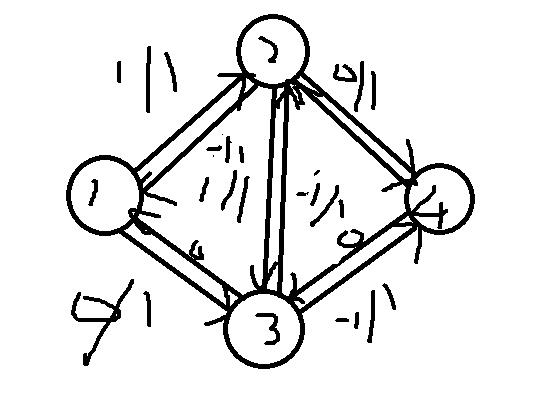
于是，我们又找到了一条新的増广路：1——3——2——4

（因为0-（-1）=1，所以这条边也可以走）

那么答案是1+1=2

那么问题来了，为什么这样就算一种呢？

因为制造相反边，如2——3，就是相当于吧原来从而流到3的量流回来了。

这样就可以求出最大值。

口胡内容就到这里，其实我写的不是很清楚，大家看刘汝佳的可能会更清楚一些，但是重点来了！！！

这道题代码实现非常之困难，至少对于我来说，所以刘汝佳的代码我压根没看懂。

因此，我自己写得一份浅显易懂的代码

没有vector！！！没有指针！！！

而且有复杂的注释！！！

#include <iostream>
#include <cmath>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
#include <queue>
using namespace std;
int n,m;//n个点，m条边 
int head[100010];//这是邻接表的标志，head[i]表示以i为顶点的第一条边 
struct edge
{
    int cap,flow;//cap为容量，flow为流量 
    int from,to;//一条边的起点终点 
    int next;//和这条边起点相同的下一条边（邻接表标志） 
}map[100010];
int index=-1;//邻接表输入数组 
int flag=0;//退出的标记 
void build_edge(int a,int b,int c)//构造邻接表，插入连接表 
{
    index++;
    map[index].from=a;
    map[index].to=b;
    map[index].cap=c;
    map[index].flow=0;
    map[index].next=head[a];
    head[a]=index;
    index++;
    map[index].from=b;//插入相反边 
    map[index].to=a;
    map[index].cap=0;
    map[index].flow=0;
    map[index].next=head[b];
    head[b]=index;
    return ;
}
int bfs()//运用bfs找到増广路 
{
    int min_flow[100010];//min_flow[i]代表到第i好点时，当前所走过变的容量-流量的最小值 
    memset(min_flow,0,sizeof(min_flow));
    queue<int> Q;//用队列 维护 
    min_flow[1]=999999;//开始为无限大 
    int p[100010];//这个很重要，构造增光路时，记录当前点是由那条边找到的，以此找到増广路时能从终点以此到起点的边的流量加上最小值 
    p[1]=-1;
    Q.push(1);//起点入队 
    while(!Q.empty())
    {
        int now=Q.front();
        Q.pop();
        for(int e=head[now];e!=-1;e=map[e].next)//邻接表枚举当前点的所有连边 
        {
            int v=map[e].cap-map[e].flow;//v就是为当前边容量-流量 
            if(v>0 && !min_flow[map[e].to])//当v>0 并且这个点没有访问过时 
            {
                p[map[e].to]=e;//记录到达这个点的边的序号 
                min_flow[map[e].to]=min(min_flow[now],v);//维护最小值 
                Q.push(map[e].to);//维护bfs 
            }
        }
        if(min_flow[n]!=0)//如果终点得到更新，说明找到増广路，直接break 
            break;
    }
    if(min_flow[n]==0)//当没有更新到终点，也就是重点最小增加值为0时，说明没有増广路了，直接完事 
        flag=1;
    for(int e=n;;e=map[p[e]].from)//从终点开始，以此倒着走増广路，把沿途上边的流量都加上终点最小更新值 
    {
        if(p[e]==-1)//如果到头就完事 
            break;
         map[p[e]].flow+=min_flow[n];//流量加上最小更新至 
         map[p[e]^1].flow-=min_flow[n];//反向边减去 
    }
    return min_flow[n];//返回最小更新至，加到答案当中 
}
int max_flow()
{
    int flow=0;//这就是神圣的答案 
    while(1)
    {
        flow+=bfs();//循环搜索 
        if(flag==1)//没有増广路，就直接跳出 
            break;
    }
    return flow;//返回答案 
}
int main()
{
    cin>>n>>m;
    for(int i=0;i<=m;i++)//初始化，很重要，制胜之点 
    {
        map[i].next=-1; 
        head[i]=-1;
    }
    for(int i=1;i<=m;i++)//读入，构造邻接表 
    {
        int a,b,c,d;
        cin>>a>>b>>c;
        build_edge(a,b,c);
    }
    cout<<max_flow();//输出答案 
}
/*
测试数据 
4 4
1 2 2
2 4 2
1 3 3
3 4 1
*/

学信息不易，作业还没动，求关注！！！