[2017BUAA软工]第一次个人项目 数独的生成与求解
Posted xxrxxr
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了[2017BUAA软工]第一次个人项目 数独的生成与求解相关的知识,希望对你有一定的参考价值。
零.Github链接
https://github.com/xxr5566833/sudo
一.PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 10 | |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 120 | |
| · Design Spec | · 生成设计文档 | 60 | |
| · Design Review | · 设计复审 (和同事审核设计文档) | 30 | |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | |
| · Design | · 具体设计 | 30 | |
| · Coding | · 具体编码 | 600 | |
| · Code Review | · 代码复审 | 300 | |
| · Test | · 测试(自我测试,修改代码,提交修改) | 200 | |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 120 | |
| · Size Measurement | · 计算工作量 | 10 | |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | |
| 合计 | 1540 |
二.解题思路描述
这道题一共有两个部分,一部分是生成数独终局,另一部分是解决给定数独问题,两者都要把最后的数独结果输出到文件中。
1.数独生成
数独生成一开始就想到用递归回溯的方法搜索所有的可行解,具体思路也不细说了,就是对每一个需要填的空搜索可行解,之后的很长一段时间我都是在优化这个算法,但是速度还是一直很慢,所以后来又和同学讨论出了另外一个方法,就是使用数独模板和行列交换的方法产生数独,速度提高了很多很多。下面分别描述这两部分。
(1)递归方法生成数独终局
这里我没有选用普通的从(0,0)开始一直搜索到(8,8)。我的搜索的过程是:按照确定好的填入数字的顺序,对每个3*3的小九宫格的确定这个数字在这个小九宫格中的位置。这样做相比于原来的一个空一个空的搜索,我觉得好处是:通过自己确定填入小九宫格的顺序和要填入的数字的顺序,可以保证每次填入的位置所在的3*3的小九宫格一定没有包含当前这个数字,这样在判断是否可以填入时,只需要判断当前行的列的情况就可以了。
但是递归算法速度还是很慢,即使我一直在优化,最后生成一百万个数独的时间还是很长。于是我通过和其他人讨论,也参考了大家在群里的讨论,同时也参考了《编程之美》,确定了另一种数独的生成算法。
(2)通过模板和行列交换生成数独终局
这个方法可以分为两个部分:
①通过第一行数字和模板,产生一个原始的数独矩阵;
②通过对这个数独矩阵的行和列进行局部交换,产生符合数独要求的不同数独矩阵。
下面就分这两部分叙述。
产生原始数独矩阵:
| a | b | c | d | e | f | g | h | i |
| d | e | f | g | h | i | a | b | c |
| g | h | i | a | b | c | d | e | f |
| b | a | d | c | f | e | h | i | g |
| c | f | e | h | i | g | b | a | d |
| h | i | g | b | a | d | c | f | e |
| e | c | a | f | d | b | i | g | h |
| f | d | b | i | g | h | e | c | a |
| i | g | h | e | c | a | f | d | b |
这是一个模板,其中的a~i分别表示一个数字。如果我能确定好第一行,那么通过这个模板映射关系,我们就可以由第一行生成2~9行。具体的映射关系可以这样描述:假如第一行是(9,8,7,6,5,4,3,2,1),那么数字9就对应了上面模板的字母a,然后我们通过这个模板可以确定字母a在第二行的第7个格子里(从1开始算起),所以我们就能确定第二行的数字9的位置是在第6个格子。之后的每个数字同理,确定了第二行的数字后,继而可以确认第三行,第四行...最后就可以得到原始的数独矩阵。
可以看出原始矩阵的生成是通过第一行的排列情况和模板确定的,其中模板是确定不变的,而我们可以通过改变第一行的排列情况来产生不同的原始矩阵。具体的第一行的情况总数就是8个数字的全排列数量(第一个数字是确定的,所以只需要排列其他的数字)。
这样可以生成8!=40320种不同的原始数独矩阵,还不够题目中的最大数量要求。我们还需要通过行列变换来产生不同的数独矩阵。
行列变换:
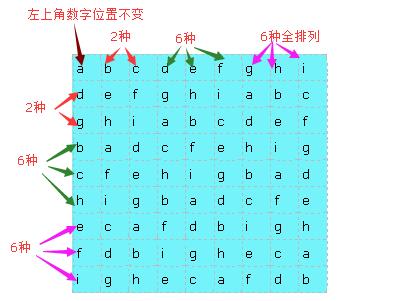
对于通过模板和第一行生成的原始数独矩阵,我们可以通过局部的行列变换来生成更多的矩阵。我的变换方法是:
①左上角这个数字的位置不能变,每次交换是交换整个一行或者整个一列;
②把9行分为三个大行,第一个大行包括第2行和第3行,这时可以选择交换第2行和第3行,所以第一个大行有2种情况。第二个大行包括第4,5,6行,此时这三行的每一种全排列 交换情况都可以,比如我可以通过交换让第二个大行变成(4,6,5),所以第二个大行有6种,同理第三个大行也有6种。
③这9列也同理,分为三个大列,和行一样,分别有2种,6种和6种排列情况。
④不同的交换情况是相互独立的!即某一部分行列的交换不会影响其他的行和列的交换情况数量的增减,所以根据排列组合知识,我们可以得到总的情况数是每一种行列变换情 况数的乘积。
所以我们可以得到,对于每一个原始矩阵,我们可以产生2*2*6*6*6*6种数独矩阵,而原始数独矩阵的产生,即之前说的第一个过程和这里的行列交换是互相独立的,所以一共的情况数是8!*4*6*6*6*6,已经可以达到题目的要求了。
模板加行列变换生成数独算法的思考:
这样做确实生成速度快,但是我们还是需要审视这个算法,它到底满不满足两个条件:
①生成的数独矩阵都是合法的吗?
②生成的数独矩阵都是不重复的吗?
下面我们从这两个部分证明一下:
首先需要确定生成的数独矩阵都合法吗?合法的数独需要满足3个条件:
①每一行1-9这九个数字有且仅有一个
②每一列1-9这九个数字有且仅有一个
③每个3*3的九宫格中1-9这九个数字有且仅有一个
审视我们之前的这个算法,假设变换前是合法的数独,先看行变换:
①先看行变换后是否符合数独合法性。因为每个行变换都是在整个行的基础上变换,因为原来这个行就满足条件,所以变换后肯定也满足行的条件。
②因为每个行变换,仅仅影响每个数字在所在列的位置,但是仍然满足每个列每个数字仅仅出现一次,所以行变换后也满足列的条件
③因为每个行变换都是在一个大行的范围内排列的,一个大行就是之前说的把1-9行分为1-3,4-6,7-9这三个大行,所以在大行内无论怎么交换,仅仅改变每个数字在其九宫格内 内的位置,并不影响原来就满足的九宫格条件。
所以综上,一个合法数独经过行变换并不会违反数独的条件,同理,列变换也不会违反数独的条件。而行变换和列变换之间是互相独立的,所以综上,行变换,列变换和行列变换的组合都不会违反数独的条件。
然后要确定这样产生的数独矩阵不会重复。两个数独矩阵重复意味着这两个数独矩阵每个位置上的数字都相等。关于不会重复的证明,不如就按照之前说的两步操作①产生原始数独矩阵②行列变换来证明。
很容易就可以得到的是:对于一个原始数独矩阵,对它进行不同的行列变换,得到的数独矩阵是不同的。
我们不妨把数独的生成过程倒过来,我们先通过对模板进行行列变换,那么对于不同的行列变换,我们一定可以得到不同的模板矩阵。例如下图就是上面那个模板矩阵交换了第二列和第三列后生成新的模板。
| a | c | b | d | e | f | g | h | i |
| d | f | e | g | h | i | a | b | c |
| g | i | h | a | b | c | d | e | f |
| b | d |
a | c | f | e | h | i | g |
| c | e | f | h | i | g | b | a |
d |
| h | g | i | b | a |
d | c | f | e |
| e | a | c | f | d | b | i | g | h |
| f | b | d | i | g | h | e | c | a |
| i | h | g | e | c | a | f | d | b |
然后我们建立a~i和1~9的一 一映射关系,这样的映射关系考虑到第一个数字是固定的,那么一共有8!种不同的映射关系。
而对于一个模板矩阵来说,不同的映射关系,一定会产生不同的数独矩阵。
前面的其实都很好理解,即很容易知道①对于原始的模板,不同的行列变换,最后产生的模板矩阵不一样②对于一个产生的模板矩阵,不同的映射关系,产生的数独也不一样。那么对于不同的模板矩阵,不同的映射关系得到的数独矩阵一定不同吗?这个问题我一开始是不确定的,我怀疑可能会有某种模板和某种映射的组合会与另外一种模板和另外一种映射的组合最后产生的数独矩阵是一样的。
在通过举了一些例子后,我发现原来预想的重复情况没有发生,但是严谨的证明我现在还没有完整的推导出来...等我想清楚了再补充吧。
所以这个生成算法的不重复性目前我还不太能保证...
2.数独求解
我所使用数独的求解算法就是递归的搜索算法。通过搜索每一个空的可行解来完成整个数独。
但是一开始这样很慢,于是我便加入了预处理的过程,即一开始多次遍历整个数独,把那些可能的取值只有一个的空先填上,然后再递归回溯。
但是这样改进对于很多一开始找不到某个空有唯一解的数独来说是没有用的,整个算法还是很慢,之后我便用了VS带的性能分析工具,发现整个搜索过程耗费时间最多是我的判断是否可以填入的函数。我一开始的判断是否可以填入的函数是通过遍历这个空所在的行,列,3*3九宫格来确定是否可以填入的,经过思考后作出了改进:我通过建立三个数组,分别记录某一行/某一列/某个九宫格 这个数字是否可以填入。在进行填入/清除操作时,更新这三个数组,在判断是否可以填入时,直接根据这三个数组来判断,这样增加了一点空间消耗,但是减少了很多时间花费。
三.设计实现过程
1.代码组织
这里我设计了两个类,一个是数独的生成类,另一个是数独的求解类,这两个类是相互独立的,分别用于数独的求解和生成。
一开始接触C++,很多特性还不会运用,而且因为之前优化速度花了很大的时间,导致没有太多时间提升代码的维护性和扩展性,同时代码中函数之间的耦合性还是很大,因为没时间修改了,怕修改会影响正确性,所以这里把问题列举一下,以后修改:
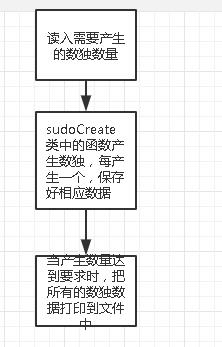
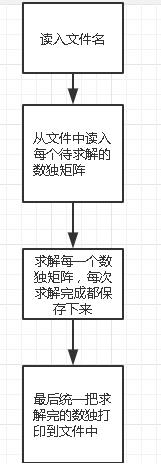
(1)数独生成过程耦合性大。我的数独生成过程是这样的:

但是第一行的全排列的生成函数目前和原始数独的生成函数耦合在一起,即每生成一个新的全排列就会直接调用原始数独的生成函数:
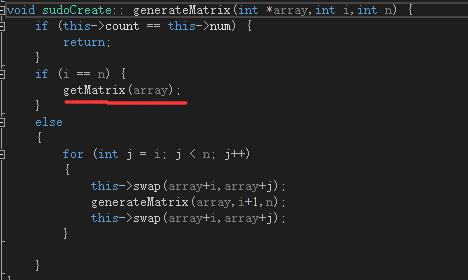
好的解决办法应该是,把每个生成的全排列记录下来,然后在生成原始矩阵时取出来用就好。
(2)空间开销过大。在实现时我进行了很多次的数独矩阵的保存操作,比如从文件中读入一个待求解矩阵后,我还把它copy到数独解决类的一个成员变量里。其实很多时候是不需要保存的,但是因为自己的指针还有内存的基础知识欠缺吧,总是想着进行冗余的复制操作以保证结果的正确性。现在我对这方面的改进做出如下计划:
①对于数独的生成,一开始为了追求效率,把所有的矩阵都生成好以后,把它们整个放入一个字符串缓存中一次写入文件。虽然这样加快了速度,但是完全可以每一次生成好一个矩阵后就进行写入操作,这样空间开销大大降低。数独的解决同理
②很多地方的数独的copy都是没有必要的,有两处:一是从文件中读入数独矩阵时,完全可以直接读到数独解决类的成员变量中,而我却先把它读到一个二维数组,然后在生成数独解决对象时又把这个二维数组中的值复制到对象的成员变量中;
(3)类中成员函数和成员变量还有冗余,其中C++的先声明再定义的特性还是优点不太适应。
2.单元测试的设计
对于单元测试目前我设计了关于下面这些功能的检测:
(1)测试了数独的生成算法是否可以生成不重复的数独。这里使用了字典树的方法。
(2)测试了数独解决算法中用到的辅助函数,包括①判断是否可以被填入②填入函数③清除函数。
四.改进程序性能
我在提高程序的速度上花了很多的功夫,以至于现在的程序空间消耗过大了...
1.提高生成数独的速度
生成数独整个过程其实可以分成两个部分:生成100万个数独,把这100万个数独存入文件。
生成100万个数独我用过两种方法:①递归回溯②模板加行列交换
写入文件我用了三种方法:①每生成一个数独,就写入文件中,而且写入是每次都调用fprintf写入一个字符或者一个数字②先把每次要写入的数独矩阵存在一个字符串缓存中,然后一次用fprintf存入③把整个100万个矩阵存在一个字符串中,最后用fprintf一次写入④改用fstream写入文件。
一开始我是用递归回溯方法生成数独,而且每次生成一个矩阵就一个字符一个数字的写入到文件中。当然这样做特别慢,即使我优化了递归回溯的过程,生成整个100万个数独矩阵并写入还是需要花费2分钟左右
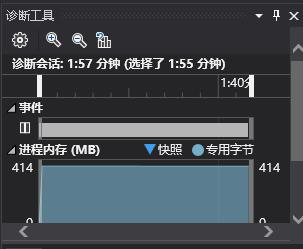
然后我通过VS的性能探测工具,发现了原来花费时间最多的是IO:
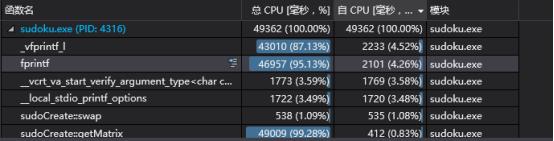
(可以看到fprintf占CPU时间比重大)
然后我就看到大家在群里的讨论,自己也和同学进行了讨论,把写入过程修改为把整个数独矩阵放在一个字符串中,然后调用fprintf写入,这样一改,果然快多了!现在整个时间开销仅仅需要17s左右。其中IO大概花费11s左右
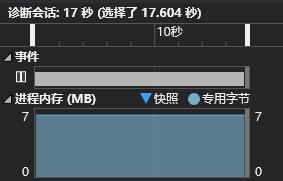
(使用递归回溯算法+把数独矩阵放入字符串中用fprintf写入)
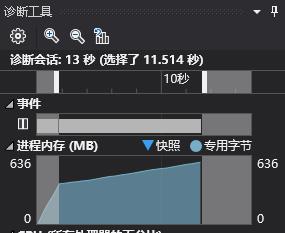
(把整个数独矩阵放入字符串中写入 100万个需要的花费时间)
然后我尝试把100万个矩阵放在一个字符串中,在生成完后一次写入...IO时间的花费更少了,需要9s
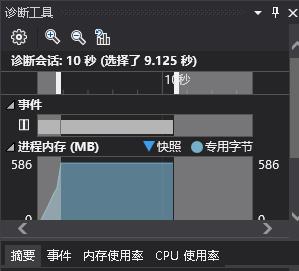
(把100万个数独矩阵放在一个字符串中调用fprintf一次写入)
最后我听取了别人的意见,转而使用fstream把100万个数独矩阵一次性写入文件中,最后的时间花费更少了,仅仅需要4s
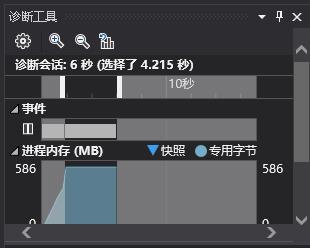
上面都是对IO的优化,下面讲对数独生成算法的优化。数独生成算法一开始我用的是递归回溯算法,即使优化了很多,但是速度还是很慢。于是我就选择之前说的模板+等价交换的方法,产生的数独速度大大提高了。现在仅仅需要2s内就可以生成100万个数独终局(不包含文件写入)
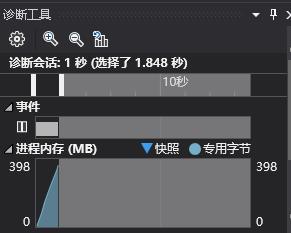
现在整个过程所需要的时间可以达到4s
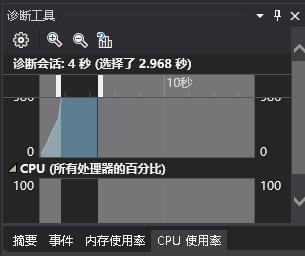
然后还可以通过开编译优化,进一步提高速度。
生成可以达到1s以内,写入可以在3s,感觉编译优化后对IO性能提升不算很大?但是生成速度提高了很多。
2.提高解决数独的速度
我选择的解决数独的算法就是递归回溯,我也没有具体的优化太多数独的解决算法,时间都用在优化数独生成了...所以这里我所做的优化就是加了一个预处理的过程,这个预处理过程其实就是先遍历整个数独的未填的空,如果能找到某个空只有一种选择,那么就可以直接填进去了。然后继续遍历整个数独矩阵直到整个数独矩阵没有可以直接填入的空格,然后开始进行递归回溯。
其实这个预处理对于简单的数独可能会提高速度,但是如果这个没有这样的只有一个选择的空格可以填,那么这个预处理过程其实是无用的。
之后要研究一下用DLX解决数独问题。
五.代码说明
核心代码有两部分,一部分是数独的生成算法,另一部分是数独的解决算法。
(1)数独的生成算法:
1 void sudoCreate::getMatrix(int array[8]) 2 { 3 this->matrix[0][0] = 3; //(0,0)上数字固定为3 4 for (int i = 1; i < 9; i++) { 5 this->matrix[0][i] = array[i - 1]; 6 } 7 /*根据map的关系和第一行的某个排列生成其他行*/ 8 for (int i = 1; i < 9; i++) { 9 for (int j = 0; j < 9; j++) { 10 this->matrix[i][j] = this->matrix[0][map[i * 9 + j]-1]; 11 } 12 } 13 /*使用多层for循环产生行和列不同交换情况的组合 14 具体是这样的:(从第0列开始) 15 第一层循环是用于是否交换第1列和第2列 16 第二层循环是用于第3,4,5列的不同排列情况,从(3,4,5)产生全排列序列可以这么交换: 17 (3,4,5)交换(1,2)列得到(3,5,4) 18 (3,5,4)交换(0,1)列得到(5,3,4) 19 (5,3,4)交换(1,2)列得到(5,4,3) 20 (5,4,3)交换(0,1)列得到(4,5,3) 21 (4,5,3)交换(1,2)列得到(4,3,5) 22 (4,3,5)交换(0,1)列得到(3,4,5) 23 可以生成整个全排列并恢复为原来的状态 24 这也是下面的switch语句的含义 25 之后几层循环同理 26 */ 27 for (int i1 = 0; i1 < 2; i1++) { 28 switch (i1) { 29 case 0: 30 case 1: 31 for (int j = 0; j < 9; j++) { 32 this->swap(&(matrix[j][1]),&(matrix[j][2])); 33 } 34 break; 35 default: 36 break; 37 } 38 for (int i2 = 0; i2 < 6; i2++) { 39 switch (i2) { 40 case 1: 41 case 3: 42 case 5: 43 for (int j = 0; j < 9; j++) { 44 this->swap(&(matrix[j][3]),&(matrix[j][4])); 45 } 46 break; 47 case 0: 48 case 2: 49 case 4: 50 for (int j = 0; j < 9; j++) { 51 this->swap(&(matrix[j][4]),&(matrix[j][5])); 52 } 53 break; 54 default: 55 break; 56 } 57 for (int i3 = 0; i3 < 6; i3++) { 58 switch (i3) { 59 case 1: 60 case 3: 61 case 5: 62 for (int j = 0; j < 9; j++) { 63 this->swap(&(matrix[j][6]), &(matrix[j][7])); 64 } 65 break; 66 case 0: 67 case 2: 68 case 4: 69 for (int j = 0; j < 9; j++) { 70 this->swap(&(matrix[j][7]), &(matrix[j][8])); 71 } 72 break; 73 74 default: 75 break; 76 } 77 for (int i4 = 0; i4 < 2; i4++) { 78 switch (i4) { 79 case 0: 80 case 1: 81 for (int j = 0; j < 9; j++) { 82 this->swap(&(matrix[1][j]), &(matrix[2][j])); 83 } 84 break; 85 default: 86 break; 87 } 88 for (int i5 = 0; i5 < 6; i5++) { 89 switch (i5) { 90 case 1: 91 case 3: 92 case 5: 93 for (int j = 0; j < 9; j++) { 94 this->swap(&(matrix[3][j]), &(matrix[4][j])); 95 } 96 break; 97 case 0: 98 case 2: 99 case 4: 100 for (int j = 0; j < 9; j++) { 101 this->swap(&(matrix[4][j]), &(matrix[5][j])); 102 } 103 break; 104 105 default: 106 break; 107 } 108 /*将产生的矩阵存好*/ 109 int* newmatrix = (int *)malloc(81*sizeof(int)); 110 for (int i = 0; i < 9; i++) 111 for (int j = 0; j < 9; j++) 112 newmatrix[i*9+j] = this->matrix[i][j]; 113 matrixarray[count] =newmatrix; 114 this->count++; 115 116 if (this->count == this->num) { 117 return ; 118 } 119 120 } 121 } 122 } 123 } 124 } 125 return ; 126 }
这里需要注意的是,用for循环来实现某几行或者几列的全排列时,需要注意交换的顺序。这里我一开始想错了,因为我一开始是通过for循环的循环变量来决定当前该如何交换,比如我可以设置(1,2,3)的全排列和数字0-5这样的映射关系:0 对应 (1,2,3) 1 对应 (1,3,2) 2对应(2,1,3)等等以此类推,所以我可以根据当前的for循环的变量是多少,来决定如何交换。
但是我们是直接在这个数独矩阵上进行交换的,所以在进行下一次交换时,使用的数独矩阵是上一次交换过的,所以不能错误的认为交换都发生在原始的矩阵上。
(2)数独的解决算法
void sudoSolver:: solve(int arrayindex) { if (this->solved == true) return; if (arrayindex > maxempty - 1) { this->solved = true; int* newmatrix = (int *)malloc(81 * sizeof(int)); for (int i = 0; i < 9; i++) for (int j = 0; j < 9; j++) newmatrix[i * 9 + j] = this->matrix[i][j]; this->matrixarray[count] = newmatrix; count++; return; } int i = rchoice[arrayindex]; int j = cchoice[arrayindex]; // print(this->matrix); for (BUAA软工个人作业Week2-代码复审