17南宁网络赛
Posted yijiull
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了17南宁网络赛相关的知识，希望对你有一定的参考价值。
G. Finding the Radius for an Inserted Circle
题目:链接
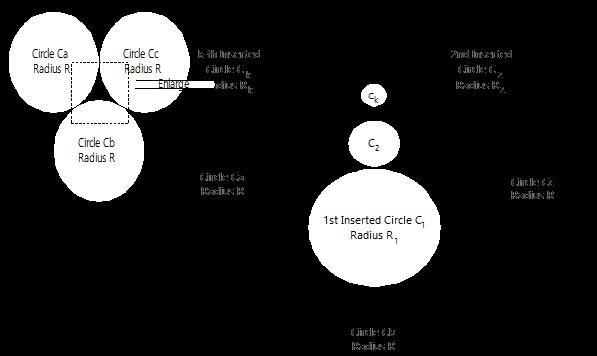
让求第k个内切圆的半径 r[k]
这题我们没做出来,主要是因为我发现的太晚了......
一开始看到的时候觉得图看起来太复杂就没去看....
最后还剩二十分钟的时候开始做,本来应该也是可以过的,结果读错输入格式了,然后就悲剧了...... 差点完成绝杀啊!!!
根据勾股定理很容易推出公式 r[i] = (√3 * R - R - 2 * c[i-1] )2 / ( 2 * √3 * R - 4 * c[i-1] )
其中 c[i] 是 r[i] 的前缀和.
1 #include <bits/stdc++.h> 2 using namespace std; 3 double r[23]; 4 double c[23]; 5 int main(){ 6 int t; 7 //freopen("in.txt","r",stdin); 8 scanf("%d",&t); 9 for(int i =0; i<=11;i++){ 10 r[i]=c[i]=0; 11 } 12 double R; 13 int k; 14 scanf("%lf", &R); 15 for(int i = 1; i <= 10; i++){ 16 double temp = (sqrt(3)-1)*R - 2*c[i-1]; 17 r[i]=temp/(2*sqrt(3)*R-4*c[i-1])*temp; 18 c[i]=c[i-1]+r[i]; 19 } 20 while(t--) { 21 scanf("%d", &k); 22 int a=r[k]; 23 printf("%d %d\\n",k, a); 24 } 25 scanf("%d",&k); 26 return 0; 27 }
发现大家好像都不是很爱会几何题的样子~
F. Overlapping Rectangles
题意:给n个矩形, 让求面积并.
之前做过的一道题,离散化 + 扫描线 + 线段树....
可是还是浪费了很多时间,因为昨天做了和这个很相似的题目,只不过那个是让找任意多边形面积的边界,思路就跑偏了,这题矩形比较特殊直接线段树+扫描线搞定~
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #define lson l,m,rt<<1 5 #define rson m,r,rt<<1|1 6 using namespace std; 7 const int maxn=2210; //需要离散的x坐标数 8 int cnt[maxn<<2]; //标记该线段是否被选 9 double sum[maxn<<2]; //被选择的部分线段总长度 10 double X[maxn<<2]; //离散化 11 struct seg 12 { 13 double l,r; 14 double h; 15 int s; //标记 16 seg(){} 17 seg(double l,double r,double h,int s):l(l),r(r),h(h),s(s){} 18 bool operator < (const seg &cmp) const 19 { 20 return h<cmp.h; 21 } 22 }ss[maxn]; 23 24 void pushup(int rt,int l,int r) 25 { 26 if(cnt[rt]) sum[rt]=X[r]-X[l]; //如果该线段标记被完全选择，则长度为全长。。 27 else if(l+1==r) sum[rt]=0; //若未被完全选择，且该线段只有一段，则长度为0 28 else sum[rt]=sum[rt<<1]+sum[rt<<1|1]; //未被完全选择，且不止一段，则长度为被选择的部分 29 } 30 31 void update(int L,int R,int c,int l,int r,int rt) 32 { 33 if(L<=l&&r<=R) 34 { 35 cnt[rt]+=c; // 选则或者删除一次该线段 36 pushup(rt,l,r); 37 return ; 38 } 39 int m=(l+r)>>1; 40 if(L<m) update(L,R,c,lson); 41 if(m<R) update(L,R,c,rson); 42 pushup(rt,l,r); 43 } 44 int BIN(double key,int n,double X[]) 45 { 46 int l=0,r=n-1; 47 while(l<=r) 48 { 49 int m=(l+r)>>1; 50 if(X[m]==key) return m; 51 if(X[m]<key) l=m+1; 52 else r=m-1; 53 } 54 return -1; 55 } 56 int main() 57 { 58 int n,cas=0; 59 //freopen("in.txt", "r", stdin); 60 while(scanf("%d",&n)&&n) 61 { 62 int m=0; 63 while(n--) 64 { 65 double a,b,c,d; 66 scanf("%lf%lf%lf%lf",&a,&b,&c,&d); 67 X[m]=a; 68 ss[m++]=seg(a,c,b,1); 69 X[m]=c; 70 ss[m++]=seg(a,c,d,-1); 71 } 72 sort(X,X+m); 73 sort(ss,ss+m); 74 //离散化 75 int k=1; 76 for(int i=1;i<m;i++) 77 if(X[i]!=X[i-1]) X[k++]=X[i]; 78 79 memset(cnt,0,sizeof(cnt)); 80 memset(sum,0,sizeof(sum)); 81 double ans=0; 82 for(int i=0;i<m-1;i++) //最上面的线段不用处理 83 { 84 int l=BIN(ss[i].l,k,X); 85 int r=BIN(ss[i].r,k,X); 86 if(l<r) update(l,r,ss[i].s,0,k-1,1); 87 ans+=sum[1]*(ss[i+1].h-ss[i].h); 88 } 89 printf("%.0lf\\n",ans); 90 } 91 puts("*"); 92 return 0; 93 }
B. Train Seats Reservation
题意: 告诉每批人上下车的站点,问公交车最少安排多少个座位.
本来想着扫描线,数据比较小,直接暴力~
1 #include <bits/stdc++.h> 2 using namespace std; 3 int a[110]; 4 int main(){ 5 int n; 6 int s,t,k; 7 while(scanf("%d", &n) && n) { 8 memset(a, 0, sizeof(a)); 9 for(int i = 0; i < n; i++){ 10 scanf("%d %d %d", &s, &t, &k); 11 for(int j = s; j < t; j++) a[j]+=k; 12 } 13 int ans = 0; 14 for(int i = 1; i <= 100; i++) 15 ans = max(a[i], ans); 16 printf("%d\\n", ans); 17 } 18 puts("*"); 19 return 0; 20 }
M. Frequent Subsets Problem
1 #include <bits/stdc++.h> 2 using namespace std; 3 int n; 4 double r; 5 int a[1<<21]; 6 7 int check(int sum, int x) { 8 for(int i = 1; i <= sum; i <<= 1) { 9 if((i&x) && (!(sum&i))) return 0; 10 } 11 return 1; 12 } 13 int main(){ 14 scanf("%d %lf", &n, &r); 15 getchar(); 16 string s; 17 int k=0; 18 while(getline(cin,s)){ 19 k++; 20 istringstream ss(s); 21 int x, sum = 0; 22 while(ss>>x) { 23 x--; 24 sum += (1<<x); 25 } 26 for(int i = 1; i <= sum; i++){ 27 if(check(sum,i)) a[i]++; 28 } 29 } 30 k = ceil(k * r); 31 n = (1<<n); 32 int res = 0; 33 for(int i = 1; i <=n; i++) if(a[i] >= k) res++; 34 printf("%d\\n", res); 35 }
L. The Heaviest Non-decreasing Subsequence Problem
题意:带权重的不下降子序列.
要用nlogn的做法
因为权重较小,直接把权拆成1.
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn = 1e6+10; 4 const int inf = 1e9+10; 5 int a[maxn], d[maxn], g[maxn]; 6 int main(){ 7 int n = 0, x; 8 while(scanf("%d", &x)!=EOF){ 9 if(x >= 10000) { 10 x -= 10000; 11 a[++n] = x; 12 a[++n] = x; 13 a[++n] = x; 14 a[++n] = x; 15 a[++n] = x; 16 } else if(x >= 0) { 17 a[++n] = x; 18 } 19 } 20 for(int i = 0; i < maxn; i++) g[i] = inf; 21 for(int i = 1; i <= n; i++) { 22 int k = upper_bound(g+1, g+maxn, a[i]) - g; 23 d[i] = k; 24 g[k] = a[i]; 25 } 26 int ans = lower_bound(g+1, g+maxn, inf) - g -1; 27 printf("%d\\n", ans); 28 }
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn = 1e6+10; 4 const int inf = 1e9+10; 5 int a[maxn], d[maxn]; 6 int main(){ 7 int n = 0, x; 8 while(scanf("%d", &x)!=EOF){ 9 if(x >= 10000) { 10 x -= 10000; 11 a[++n] = x; 12 a[++n] = x; 13 a[++n] = x; 14 a[++n] = x; 15 a[++n] = x; 16 } else if(x >= 0) { 17 a[++n] = x; 18 } 19 } 20 int len = 1; 21 d[1] = a[1]; 22 for(int i = 2; i <= n; i++) { 23 if(a[i] >= d[len]) d[++len] = a[i]; 24 else{ 25 int j = upper_bound(d+1, d+1+len, a[i]) - d; 26 d[j] = a[i]; 27 } 28 } 29 printf("%d\\n", len); 30 }
J. Minimum Distance in a Star Graph
题意: n维完全图,让求任意两点间的最短距离.
思路:
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int maxn = 15; 4 int a[maxn], b[maxn]; 5 int n; 6 int get(int x) { 7 for(int i = 0; i < n; i++) if(b[i] == x) return i; 8 } 9 int ok(){ 10 for(int i = 0; i < n; i++) { 11 if(a[i] != b[i]) return 0; 12 } 13 return 1; 14 } 15 int main(){ 16 //freopen("in.txt", "r", stdin); 17 scanf("%d", &n); 18 int t = 5; 19 int x,y; 20 while(t--) { 21 scanf("%d %d", &x, &y); 22 int pos = 0; 23 while(x) { 24 a[pos++] = x % 10; 25 x /= 10; 26 } 27 pos = 0; 28 while(y) { 29 b[pos++] = y % 10; 30 y /= 10; 31 } 32 for(int i = 0; i < n/2; i++) { 33 swap(a[i], a[n-i-1]); 34 swap(b[i], b[n-i-1]); 35 } 36 int cnt = 0; 37 while(!ok()) { 38 if(a[0] == b[0]) { 39 for(int i = n-1; i>=0; i--) { 40 if(a[i] != b[i]) { 41 swap(a[0],a[i]); 42 cnt++; 43 break; 44 } 45 } 46 } else { 47 int k = get(a[0]); 48 swap(a[0], a[k]); 49 cnt++; 50 } 51 } 52 printf("%d\\n", cnt); 53 } 54 }
C. Auction Bidding
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #include<string> 7 #include<map> 8 #include<sstream> 9 #include<vector> 10 11 using namespace std; 12 typedef long long ll; 13 const int maxn = 5005; 14 const double eps= 1e-9; 15 const int inf = 0x3f3f3f3f; 16 17 ll ans[maxn]; 18 struct node{ 19 int id; 20 int p; 21 bool operator <(const node& s) const{ 22 return p==s.p?id<s.id:p>s.p; 23 } 24 }; 25 26 vector<node> v[maxn]; 27 28 int main(){ 29 int n,m; 30 scanf("%d%d",&n,&m); 31 memset(ans,0,sizeof(ans)); 32 for(int i=1;i<=n;i++){ 33 int r; 34 scanf("%d",&r); 35 intGSM Base Station Identification 2017南宁网络赛2017 ACM-ICPC 亚洲区（南宁赛区）网络赛 Overlapping Rectangles 矩形并面积和
2017ICPC南宁赛区网络赛 The Heaviest Non-decreasing Subsequence Problem （最长不下降子序列）
2017 ACM-ICPC 亚洲区（南宁赛区）网络赛 GSM Base Station Identification (点在多边形内模板)