最小二乘法小结

Posted 2020-10-08 迈克老狼2012

原帖地址：http://www.cnblogs.com/pinard/p/5976811.html

     最小二乘法是用来做函数拟合或者求函数极值的方法。在机器学习，尤其是回归模型中，经常可以看到最小二乘法的身影，这里就对最小二乘法的认知做一个小结。

1.最小二乘法的原理与要解决的问题　

　　　　最小二乘法是由勒让德在19世纪发现的，原理的一般形式很简单，当然发现的过程是非常艰难的。形式如下式：

　　　　　　目标函数 = Σ（观测值-理论值）²

　　　　观测值就是我们的多组样本，理论值就是我们的假设拟合函数。目标函数也就是在机器学习中常说的损失函数，我们的目标是得到使目标函数最小化时候的拟合函数的模型。举一个最简单的线性回归的简单例子，比如我们有m个只有一个特征的样本：

\\[(x^{(1)},y^{(1)}), (x^{(2)},y^{(2)},...(x^{(m)},y^{(m)})\\]

　　　　样本采用下面的拟合函数：

\\[h_\\theta(x) = \\theta_0 + \\theta_1 x\\]

　　　　这样我们的样本有一个特征\\(x\\)，对应的拟合函数有两个参数\\(\\theta_0\\)和\\(\\theta_1\\)需要求出。

　　　　我们的目标函数为：

\\[J(\\theta_0, \\theta_1) = \\sum\\limits_{i=1}^{m}(y^{(i)} - h_\\theta(x^{(i)}))^2 = \\sum\\limits_{i=1}^{m}(y^{(i)} -  \\theta_0 - \\theta_1 x^{(i)})^2\\]

　　　　用最小二乘法做什么呢，使\\(J(\\theta_0, \\theta_1)\\)最小，求出使\\(J(\\theta_0, \\theta_1)\\)最小时的\\(\\theta_0\\)和\\(\\theta_1\\)，这样就得到拟合函数了。

　　　　那么，最小二乘法怎么才能使\\(J(\\theta_0, \\theta_1)\\)最小呢？

2.最小二乘法的代数法解法

　　　　上面提到要使\\(J(\\theta_0, \\theta_1)\\)最小，方法就是对\\(\\theta_0\\)和\\(\\theta_1\\)分别来求偏导数，令偏导数为0，得到一个关于\\(\\theta_0\\)和\\(\\theta_1\\)的二元方程组。求解这个二元方程组，就可以得到\\(\\theta_0\\)和\\(\\theta_1\\)的值。下面我们具体看看过程。

\\(J(\\theta_0, \\theta_1)\\)对\\(\\theta_0\\)求导，得到如下方程：

\\[\\sum\\limits_{i=1}^{m}(y^{(i)} -  \\theta_0 - \\theta_1 x^{(i)}) = 0\\]                   

\\(J(\\theta_0, \\theta_1)\\)对\\(\\theta_1\\)求导，得到如下方程：

\\[\\sum\\limits_{i=1}^{m}(y^{(i)} -  \\theta_0 - \\theta_1 x^{(i)}) x^{(i)}= 0\\]　　

　　　上面两个方程组成一个二元一次方程组，容易求出\\(\\theta_0\\)和\\(\\theta_1\\)的值：

\\[\\theta_0 = \\bigg(\\sum\\limits_{i=1}^{m}\\big(x^{(i)})^2\\sum\\limits_{i=1}^{m}y^{(i)} - \\sum\\limits_{i=1}^{m}x^{(i)}\\sum\\limits_{i=1}^{m}x^{(i)}y^{(i)}\\bigg)\\Bigg/ \\bigg(n\\sum\\limits_{i=1}^{m}\\big(x^{(i)})^2 - \\big(\\sum\\limits_{i=1}^{m}x^{(i)})^2\\bigg)\\]

\\[\\theta_1 = \\bigg(n\\sum\\limits_{i=1}^{m}x^{(i)}y^{(i)} - \\sum\\limits_{i=1}^{m}x^{(i)}\\sum\\limits_{i=1}^{m}y^{(i)}\\bigg) \\Bigg/\\bigg( n\\sum\\limits_{i=1}^{m}\\big(x^{(i)})^2 - \\big(\\sum\\limits_{i=1}^{m}x^{(i)})^2\\bigg)\\]

　　　　这个方法很容易推广到多个样本特征的线性拟合。

　　　　拟合函数表示为 \\(h_\\theta(x_1, x_2, ...x_n) = \\theta_0 + \\theta_{1}x_1 + ... + \\theta_{n}x_{n}\\), 其中\\(\\theta_i (i = 0,1,2... n)\\)为模型参数，\\(x_i (i = 0,1,2... n)\\)为每个样本的\\(n\\)个特征值。这个表示可以简化，我们增加一个特征\\(x_0=1\\) ，这样拟合函数表示为：

\\[h_\\theta(x_0, x_1, ...x_n) = \\sum\\limits_{i=0}^{n}\\theta_{i}x_{i}\\]

　　　　损失函数表示为：

\\[J(\\theta_0, \\theta_1..., \\theta_n) = \\sum\\limits_{j=1}^{m}(h_\\theta(x_0^{(j)}, x_1^{(j)}, ...x_n^{(j)}) - y^{(j)})^2 = \\sum\\limits_{j=1}^{m}((\\sum\\limits_{i=0}^{n}\\theta_{i}x_{i}^{(j)})- y^{(j)})^2\\]

　　　　利用损失函数分别对\\(\\theta_i (i=0,1,...n)\\)求导,并令导数为0可得：

\\[\\sum\\limits_{j=1}^{m}(\\sum\\limits_{i=0}^{n}\\theta_{i}x_{i}^{(j)} - y^{(j)})x_i^{(j)}=0 (i=0,1,2,…,n)\\]

　　　　这样我们得到一个\\(n+1\\)元一次方程组，这个方程组有\\(n+1\\)个方程，求解这个方程，就可以得到所有的\\(n+1\\)个未知的\\(\\theta\\)。

　　　　这个方法很容易推广到多个样本特征的非线性拟合。原理和上面的一样，都是用损失函数对各个参数求导取0，然后求解方程组得到参数值,这里就不累述了。

3.最小二乘法的矩阵法解法

　　　　矩阵法比代数法要简洁，且矩阵运算可以取代循环，所以现在很多书和机器学习库都是用矩阵法来做最小二乘法。

　　　　这里用上面的多元线性回归例子来描述矩阵法解法。

　　　　假设函数\\(h_\\theta(x_1, x_2, ...x_n) = \\theta_0 + \\theta_{1}x_1 + ... + \\theta_{n}x_{n}\\)的矩阵表达方式为：

\\[h_\\mathbf{\\theta}(\\mathbf{x}) = \\mathbf{X\\theta}\\]

　　　　其中， 假设函数\\(h_\\mathbf{\\theta}(\\mathbf{X})\\)为\\(m\\times 1\\)的向量,\\(\\mathbf{\\theta}\\)为\\(n\\times 1\\)的向量，里面有\\(n\\)个代数法的模型参数。\\(\\mathbf{X}\\)为\\(m\\times n\\)维的矩阵。\\(m\\)代表样本的个数，\\(n\\)代表样本的特征数。

　　　　损失函数定义为

\\[J(\\mathbf\\theta) = \\frac{1}{2}(\\mathbf{X\\theta} - \\mathbf{Y})^T(\\mathbf{X\\theta} - \\mathbf{Y})\\]

　　　　其中\\(\\mathbf{Y}\\)是样本的输出向量，维度为\\(m\\times 1\\), \\(\\frac{1}{2}\\)在这主要是为了求导后系数为1，方便计算。

　　　　根据最小二乘法的原理，我们要对这个损失函数对\\(\\theta\\)向量求导取0。结果如下式：

\\[\\frac{\\partial}{\\partial\\mathbf\\theta}J(\\mathbf\\theta) = \\mathbf{X}^T(\\mathbf{X\\theta} - \\mathbf{Y}) = 0\\]

　　　　

     这里面用到了矩阵求导链式法则，和三个矩阵求导的公式。

     首先把\\(（\\mathbf{X\\theta} - \\mathbf{Y})^T(\\mathbf{X\\theta} - \\mathbf{Y})\\)展开，为\\(\\theta^TX^TX\\theta-\\theta^TX^TY-Y^TX\\theta+Y^TY\\),利用下面三个公式对\\(\\theta\\)求导，即可求得上面的结果。

公式1：\\(A\\)为对称矩阵

\\[\\frac{\\partial}{\\partial\\mathbf{X}}(\\mathbf{X^TAX}) =2\\mathbf{AX}\\]

公式2：

\\[\\frac{\\partial}{\\partial\\mathbf\\theta}(\\mathbf{X\\theta}) =\\mathbf{X^T}\\]

公式3：

\\[\\frac{\\partial}{\\partial\\mathbf\\theta}(\\mathbf{\\theta^TX}) =\\mathbf{X}\\]

　　　　对上述求导等式整理后可得：

\\[\\mathbf{X^{T}X\\theta} = \\mathbf{X^{T}Y}\\]

两边同时左乘\\((\\mathbf{X^{T}X})^{-1}\\)可得：

\\[\\mathbf{\\theta} = (\\mathbf{X^{T}X})^{-1}\\mathbf{X^{T}Y}\\]

　　　　这样我们就一下子求出了\\(\\theta\\)向量表达式的公式，免去了代数法一个个去求导的麻烦。只要给了数据,我们就可以算出\\(\\theta\\)。

4.最小二乘法的局限性和适用场景　　

　　　　从上面可以看出，最小二乘法适用简洁高效，比梯度下降这样的迭代法似乎方便很多。但是这里我们就聊聊最小二乘法的局限性。

　　　　首先，最小二乘法需要计算\\(\\mathbf{X^{T}X}\\)的逆矩阵，有可能它的逆矩阵不存在，这样就没有办法直接用最小二乘法了，此时梯度下降法仍然可以使用。当然，我们可以通过对样本数据进行整理，去掉冗余特征,让\\(\\mathbf{X^{T}X}\\)的行列式不为0，然后继续使用最小二乘法。

　　　　第二，当样本特征n非常的大的时候，计算\\(\\mathbf{X^{T}X}\\)的逆矩阵是一个非常耗时的工作（nxn的矩阵求逆），甚至不可行。此时以梯度下降为代表的迭代法仍然可以使用。那这个n到底多大就不适合最小二乘法呢？如果你没有很多的分布式大数据计算资源，建议超过10000个特征就用迭代法吧,或者通过主成分分析降低特征的维度后再用最小二乘法。

　　　　第三，如果拟合函数不是线性的，这时无法使用最小二乘法，需要通过一些技巧转化为线性才能使用，此时梯度下降仍然可以用。

　　　　第四，讲一些特殊情况。当样本量m很少，小于特征数n的时候，这时拟合方程是欠定的，常用的优化方法都无法去拟合数据。当样本量m等于特征说n的时候，用方程组求解就可以了。当m大于n时，拟合方程是超定的，也就是我们常用于最小二乘法的场景了。

5.最小二乘法的例子

数据同http://www.cnblogs.com/mikewolf2002/p/7634571.html中使用的数据。

程序代码如下：

clear all; close all; clc;
x = load(\'ex2x.dat\');
y = load(\'ex2y.dat\');
figure(\'name\',\'线性回归-最小二乘法\')
plot(x,y,\'o\')
xlabel(\'年龄\')
ylabel(\'高度\')
m = length(y); % 样本数目
x = [ones(m, 1), x]; % 输入特征增加一列1作为x0
theta=inv(x\'*x)*x\'*y; %通过最小二乘法计算的矩阵来求得假设函数系数
hold on
plot(x(:,2), x*theta, \'-\') % x是两列矩阵，第二列是年龄
legend(\'训练数据\', \'线性回归\')
theta
predict1 = [1, 3.5] *theta
predict2 = [1, 7] *theta

View Code

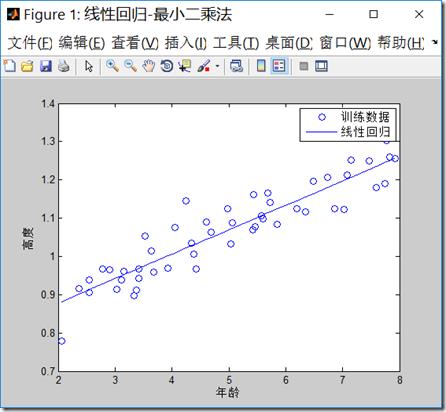
程序输出结果：

theta =

    0.7502
    0.0639


predict1 =

    0.9737


predict2 =

    1.1973

View Code