最大流最小割一题

Posted 2020-10-08 y119777

a

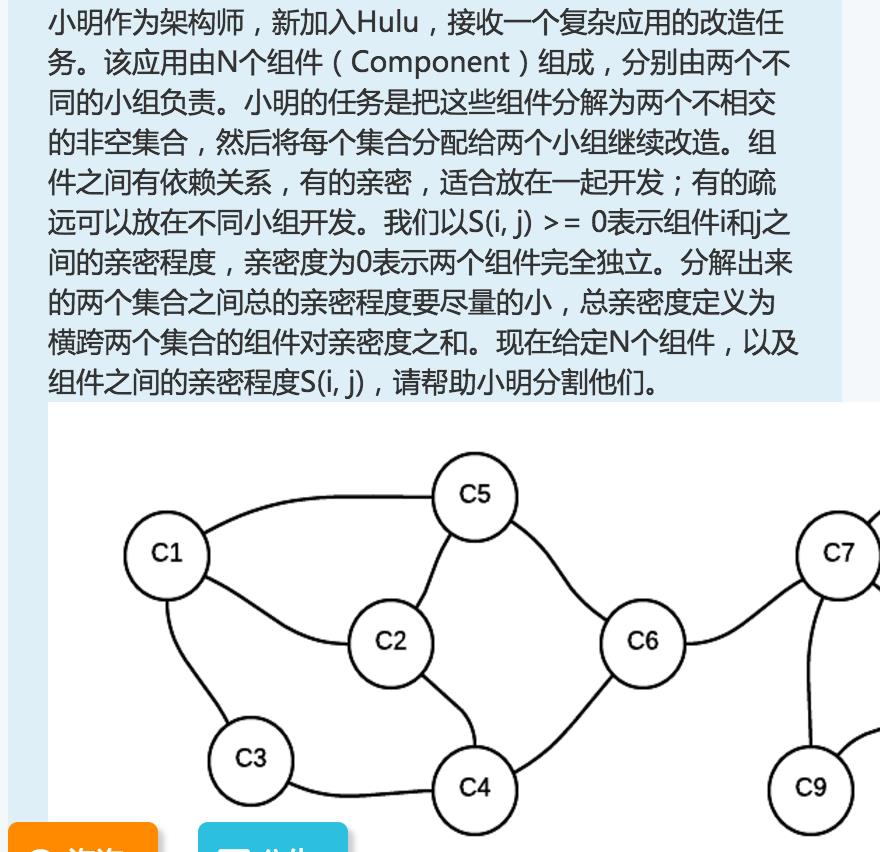
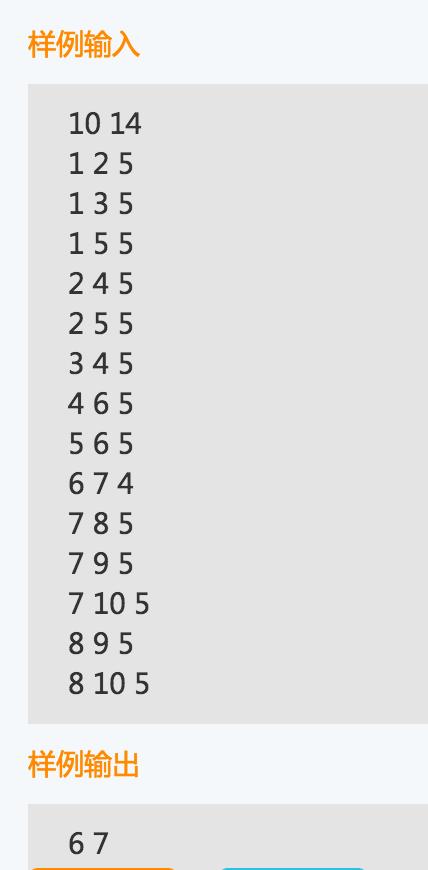
看完题目，根本没想法，暴力的复杂度是指数级别的，枚举所有的集合，当时有点紧张，暴力的都没写，其实没思路的

时候最好写暴力的算法，骗点分就可以了。后来，看了牛客网上大神的思路，然后学习了下最大流最小割的方法，这题的

做法就是枚举源点和汇点，跑最大流算法，然后用流量更新答案，同时保存最小割，最后输出，就可以了。

简单写了下，也是无法实际运行去判断正误。

对最大流最小割的思路理解的不是很透彻，不知道怎么求最小割，没有做这方面的练习。

  1 #include <iostream>
  2 #include <cstdio>
  3 #include <cstring>
  4 #include <queue>
  5 #include <cmath>
  6 #include <algorithm>
  7 using namespace std;
  8 
  9 const int mn=422;
 10 const int mm=10000;
 11 const double oo=999999;
 12 int node, st, sd, edge;
 13 int reach[mm], nxt[mm];
 14 double flow[mm];
 15 int adj[mn], work[mn], dis[mn], que[mn], cap[mn];
 16 
 17 inline void init(int _node, int _st, int _sd)
 18 {
 19     node=_node, st=_st, sd=_sd;
 20     for(int i=0; i<node; i++)
 21         adj[i]=-1;
 22     edge=0;
 23 }
 24 
 25 inline void addedge(int u, int v, double c1, double c2)
 26 {
 27     reach[edge]=v, flow[edge]=c1, nxt[edge]=adj[u], cap[edge] = c1, adj[u]=edge++;
 28     reach[edge]=u, flow[edge]=c2, nxt[edge]=adj[v], cap[edge] = c2, adj[v]=edge++;
 29 }
 30 
 31 bool bfs()
 32 {
 33     int i,u,v,l,r=0;
 34     for(i=0; i<node; ++i)dis[i]=-1;
 35     dis[que[r++]=st]=0;
 36     for(l=0; l<r; ++l)
 37         for(i=adj[u=que[l]]; i>=0; i=nxt[i])
 38             if(flow[i]&&dis[v=reach[i]]<0)
 39             {
 40                 dis[que[r++]=v]=dis[u]+1;
 41                 if(v==sd)return 1;
 42             }
 43     return 0;
 44 }
 45 typedef pair<int, int> pii;
 46 vector<pii> getCut() {
 47     int l, r = 0, u, v;
 48     que[r++] = st;
 49     vector<pii> res;
 50     vector<bool> in(node, 0);
 51     for (l = 0; l < r; l++) {
 52         if(in[que[l] ]) continue;
 53         in[que[l] ] = 1;
 54         for (int i = adj[u = que[l]]; i >= 0; i = nxt[i]) {
 55             //cout << reach[i] <<" ";
 56             if(flow[i] != 0) {
 57                 que[r++] = reach[i];
 58             } else {
 59                 int x = u, y = reach[i];
 60                 if(x > y) swap(x, y);
 61                 res.push_back({x, y});
 62             }
 63         }
 64         //cout << endl;
 65     }
 66     return res;
 67 }
 68 
 69 double dfs(int u,double exp)
 70 {
 71     if(u==sd) return exp;
 72     double  tmp;
 73     for(int &i=work[u],v; i>=0; i=nxt[i])
 74         if(flow[i]&&dis[v=reach[i]]==dis[u]+1&&(tmp=dfs(v,min(exp,flow[i])))>0)
 75         {
 76             flow[i]-=tmp;
 77             flow[i^1]+=tmp;
 78             return tmp;
 79         }
 80     return 0;
 81 }
 82 
 83 double Dinic()
 84 {
 85     double max_flow=0, flow;
 86     while(bfs())
 87     {   //cout << "asd" << endl;
 88         for(int i=0; i<node; i++)   work[i]=adj[i];
 89         while(flow=dfs(st,oo)) {
 90             //cout << flow << endl;
 91             max_flow+=flow;
 92         }
 93     }
 94     return max_flow;
 95 }
 96 //上面从网上搜索的，注意修改顶点数，边数，这里边数是2倍，注意节点的编号，从0开始。
 97 //当然，你必须知道dinic算法的逻辑才行。
 98 struct Node {
 99     int x, y, v;
100 };
101 int main()
102 {
103     freopen("test.in", "r", stdin);
104     int  n, m;
105     scanf("%d%d",&n,&m);
106     int x, y, v;
107     vector<Node> e;
108     for (int i = 0; i < m; i++) {
109         scanf("%d%d%d", &x, &y, &v);
110         e.push_back({x, y, v});
111     }
112     int res = INT_MAX;
113     vector<pii> p;
114     for (int i = 1; i <= n; i++) {
115         for (int j = i + 1; j <= n; j++) {
116             init(n + 1, i, j);
117             for (Node t : e) {
118                 addedge(t.x, t.y, t.v, t.v);
119             }
120             double ans=Dinic();
121             if(ans < res) {
122                 res = ans;
123                 p = getCut();
124             }
125         }
126     }
127     //cout << res << endl;
128     sort(p.begin(), p.end());
129     for (pii t : p)
130         cout << t.first << " " << t.second << endl;
131     return 0;
132 }

View Code