二叉树的递归遍历

Posted 2020-10-07 Dijkstra_Liu

首先，二叉树递归遍历分为先序遍历、中序遍历和后序遍历。

先序遍历为：根节点+左子树+右子树

中序遍历为：左子树+根节点+右子树

后序遍历为：左子树+右子树+根节点

（只要记住根节点在哪里就是什么遍历，且都是先左再右）

举个例子，如二叉树：

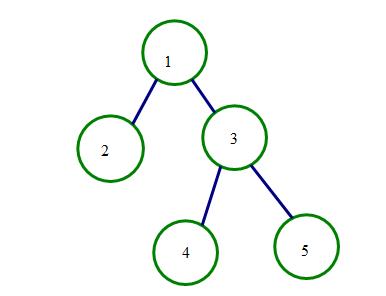
这棵树的先序遍历为：1 2 3 4 5

中序遍历为：2 1 4 3 5

后序遍历为：2 4 5 4 1

以上类容比较好理解，然后就是干活算法了

问，得知其中两个遍历，是否能构造出二叉树以求出第三个遍历？

是可以的。

首先我要说明我喜欢用的二叉树储存方式：两个数组：lefttree[]、righttree[];

其中lefttree[i]、righttree[i]代表的是根节点i的左子树和右子树(0表示没有)

例如上图为

lefttree:2 0 4 0 0

righttree:3 0 5 0 0

现在问题来了：

一、得知先序遍历和中序遍历，怎么得到二叉树？

先上数据：

5 //二叉树节点个数

1 2 3 4 5 //先序遍历

2 1 4 3 5 //中序遍历

我们知道，先序遍历的第一个永远是根节点，因此我们确切得得出1是根节点

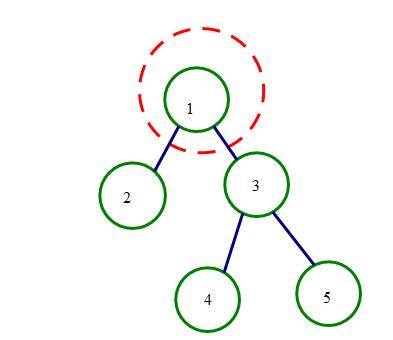
接着，我们在中序遍历终找到2，显然得出2的左边是左子树，右边是右子树。

我们递归搜索左子树，此时2为根节点，发现2的左右在中序遍历中没有数了，于是返回2到lefttree[1]里面

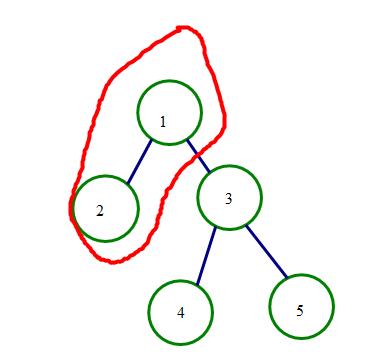
然后看先序遍历，遇到3，将3为根节点，发现在中序遍历中3的左边有4，于是递归左子树到4。

到4以后发现在中序遍历4的左右没有数了，返回lefttree[3]=4

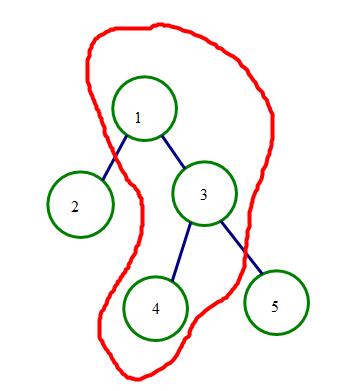
返回到3以后，发现3在中序遍历的右边有一个5，说明5是3的右子树，递归到5

发现5左右没有了，返回righttree[3]=5

3的搞完了继续返回，righttree[2]=3

然后完事大吉，看代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
int n;
int pre_order[100010];//先序遍历
int in_order[100010];//中序遍历
int lefttree[100010];//左子树
int righttree[100010];//右子树
int build(int in_left,int in_right,int pre_left,int pre_right)//主要函数，前两个参数是中序遍历从几到几的递归区间，后两个是先序遍历的。
{
    if(in_right < in_left)//此节点不存在，直接返回0
        return 0;
    int root=pre_order[pre_left];//先序遍历的第一个为根节点
    int k=in_left;
    while(in_order[k]!=root)//看当前的跟在中序遍历中的下标是多少
        k++;
    int cnt=k-in_left;//当先根的左子树节点个数
    lefttree[root]=build(in_left,k-1,pre_left+1,pre_left+cnt);//递归左子树，注意每个参数都很重要    
    righttree[root]=build(k+1,in_right,pre_left+cnt+1,pre_right);//递归右子树，参数同样重要
    return root;//返回根节点到上一个根节点的子树数组。
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)//读入
        cin>>pre_order[i];
    for(int i=1;i<=n;i++)
        cin>>in_order[i];
        build(1,n,1,n);//调用
}

以上是先中遍历构造

二、知道中序遍历后序遍历，构造二叉树

其实，这么说，这个和前面的那个很像

只不过是把先序遍历倒过来成了后序遍历

代码如下：

 

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
int n;
int in_order[100010];
int post_order[100010];
int lefttree[100010];
int righttree[100010]; 
int build(int in_left,int in_right,int post_left,int post_right)
{
    if(in_right < in_left)
        return 0;
    int root=post_order[post_right];//这里不同了
    int k=in_left;
    while(in_order[k]!=root)
        k++;
    int cnt=k-in_left;
    lefttree[root]=build(in_left,k-1,post_left,post_left+cnt-1);//这里不同了
    righttree[root]=build(k+1,in_right,post_left+cnt,post_right-1);
    return root;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
        cin>>in_order[i];
    for(int i=1;i<=n;i++)
        cin>>post_order[i];
    build(1,n,1,n);
}

谢谢大家，关于二叉树遍历的讲解就结束了，求关注！！！