树4二叉树的遍历

Posted 2020-10-07

简介

遍历二叉树就是按照某种顺序，将树中的结点都枚举一遍，且每个结点仅仅访问一次。因为树不是线性的结构，遍历不像线性表那样简单，因此他的遍历需要特点的算法来完成。

从某种角度讲，对二叉树的遍历就是将树形结构转换为线性结构的操作。

二叉树的遍历方法主要有如下几种：

• 先序遍历：先访问root结点，再先序遍历左子树，再先序遍历右子树。
• 中序遍历：先中序遍历左子树，再访问root结点，再中序遍历右子树。
• 后序遍历：先后序遍历左子树，再后序遍历右子树，再访问root结点。
• 层遍历：从上到下，从左到右，一层一层的遍历结点。

提示：

1、大多数情况下，我们总是习惯 先左后右。遍历的时候，左子树总是先于右子树，这种策略记为LR，相反的策略记为RL。本文中默认是采用LR。

2、 先序遍历，中序遍历，后序遍历都属于深度优先遍历。层遍历则属于广度优先遍历。深度优先遍历需要用栈实现（调用栈或者辅助栈），而广度优先遍历则需要用队列实现。

3、所谓的先、中、后，都是对于访问root结点的顺序来定义的。

构造一个简单的链式二叉树

先通过硬编码构建一个简单的下图所示的链式二叉树，后续的例子都是以这个为基础的。

       A
      / \\
    B   C
    / \\
  D   E

class LinkedBinaryTree
{
    /**
     * 静态内部类，结点类。
     * */
    private static class Node<T>
    {
        private T element;
        private final Node<T> left;
        private final Node<T> right;
        
        public Node(T element , Node<T> left , Node<T> right)
        {
            this.element = element;
            this.left = left;
            this.right = right;
        }

        @SuppressWarnings("unused")
        public T getElement(){
            return element;
        }

        @SuppressWarnings("unused")
        public void setElement(T element){
            this.element = element;
        }

        public Node<T> getLeft(){
            return left;
        }

        public Node<T> getRight(){
            return right;
        }

        
        @Override
        public String toString(){
            return element.toString();
        }
        
    } // class Node end
    
    private Node<Character> root = null;      //root
    
    public LinkedBinaryTree()
    {
        creatTree();
    }
    
    /**
     * 通过硬编码构造一个二叉树
     * */
    private void creatTree()
    {
         /*******************
                A
               /               B   C
             /             D   E 
         *********************/

        Node<Character> nodeC = new Node<Character>(‘C‘, null, null);
        Node<Character> nodeD = new Node<Character>(‘D‘, null, null);
        Node<Character> nodeE = new Node<Character>(‘E‘, null, null);
        
        Node<Character> nodeB = new Node<Character>(‘B‘, nodeD, nodeE);
        root  = new Node<Character>(‘A‘, nodeB, nodeC);
    }

}

 

定义一个遍历结点访问者接口

/**
 * 遍历的访问者接口。
 * 任何需要访问结点的类都需要实现这个接口,并通过函数visit实现遍历逻辑。
 * */
interface Visitor<T>
{
    void visit(T element);
}

 因此我们的遍历函数就可以定义成这样的形式： public void xxxorderTraverse(Visitor<Character>  visitor )

 

先序遍历

先序遍历：

先序遍历的特点是：对于任何一个结点，总是先访问这个结点本身，再去访问他的各个子树。

先序遍历的访问的第一个结点一定是整个树的root结点。

它不仅仅是二叉树特有的遍历方法，它对普通的一般树（generic tree）也适用，当用于遍历一般树时算法如下。

preorder(T,root):      //T 是遍历的树对象，root是T的根结点。
   visit(root);
   for each child w of root in T do
      preorder(T,w);

 

 

以下是针对二叉树的先序遍历算法。

递归伪代码（摘自维基百科）

preorder(node)
  if (node = null)
    return
  visit(node)
  preorder(node.left)       //这里可以做一下优化：先判断node.left是否不为null，再递归调用：preorder()
  preorder(node.right)      //这里可以做一下优化：先判断node.right是否不为null，再递归调用：preorder()

非递归伪代码（摘自维基百科）

preorder(node)
  if (node = null)
    return
  s ← empty stack
  s.push(node)
  while (not s.isEmpty())
    node ← s.pop()
    visit(node)
    //右子树先压栈，左子树再压栈。这样下一次出栈的时候，就先遍历左子树。
    if (node.right ≠ null)
      s.push(node.right)
    if (node.left ≠ null)
      s.push(node.left)

 

代码实现（Java）

private void _preorderTraverseRecursive(Node<Character> root , Visitor<Character> visitor )
    {
        if(root == null) return ;
        visitor.visit(root.getElement());  //访问当前root结点
        
        _preorderTraverseRecursive(root.getLeft(),visitor); //访问左子树
        _preorderTraverseRecursive(root.getRight(),visitor);//访问右子树
        
    }
    
    public void preorderTraverseRecursive(Visitor<Character> visitor)
    {
        _preorderTraverseRecursive(root,visitor);
    }

    /******************************************************************/
    

    public void preorderTraverseLoop(Visitor<Character> visitor)
    {
        if(root == null) return ;
        
        Deque<Node<Character>> stack = new LinkedList<Node<Character>>();  //使用双端队列代表栈
        stack.push(root);
        while(!stack.isEmpty()) 
        {
            Node<Character> node = stack.pop();
            visitor.visit(node.getElement());
            
            if(node.getRight()!=null) {
                stack.push(node.getRight());
            }
            if(node.getLeft()!=null) {
                stack.push(node.getLeft());
            }
        }

    }

 

中序遍历

中序遍历：

对于LR中序遍历，第一个被访问的结点一定是树的最左边的那个结点。

对于RL中序遍历，第一个被访问的结点一定是树的最右边的那个结点。

中序遍历一般只针对二叉树。

 

递归伪代码（摘自维基百科）

inorder(node)
  if (node = null)
    return
  inorder(node.left)
  visit(node)
  inorder(node.right)

非递归伪代码（摘自维基百科）

inorder(node)
  s ← empty stack
  while (not s.isEmpty() or node ≠ null)
    if (node ≠ null)
      s.push(node)
      node ← node.left
    else
      node ← s.pop()
      visit(node)
      node ← node.right

 

private void _inorderTraverseRecursive(Node<Character> root , Visitor<Character> visitor )
    {
        if(root == null) return ;
        _inorderTraverseRecursive(root.getLeft() , visitor);
        visitor.visit(root.getElement());
        _inorderTraverseRecursive(root.getRight() , visitor);
    }
    public void inorderTraverseRecursive(Visitor<Character> visitor)
    {
        _inorderTraverseRecursive(root, visitor);
    }
    
    
    /**
     * 非递归的中序遍历
     * */
    public void inorderTraverseLoop(Visitor<Character> visitor)
    {
        Deque<Node<Character>> stack = new LinkedList<Node<Character>>();  //使用双端队列代表栈
        Node<Character> node = root;
        
        while(!stack.isEmpty() || node!=null)
        {
            if(node!=null)
            {
                stack.push(node);
                node = node.getLeft();
            }
            else 
            {
                node = stack.pop();
                visitor.visit(node.getElement());
                node = node.getRight();
            }
        }
    }

 

 

后序遍历

后序遍历：

后序遍历最后一个被访问的结点一定是整个树的root结点。

后序遍历的特点是：对于任何一个结点，总是先访问这个结点的各个子树，再去访问这个结点本身。

它不仅仅是二叉树特有的遍历方法，它对普通的一般树（generic tree）也适用，当用于遍历一般树时算法如下。

postorder(T,root):      //T 是遍历的树对象，root是T的根结点。
   for each child w of root in T do
      postorder(T,w);
   visit(root);

 

后序遍历是很有作用的。

例如，我们要统计一个文件夹的占用空间大小，用内部结点表示文件夹，用叶子结点表示文件。则应该先去统计这个文件夹下的所有的文件以及子文件夹的大小，才能得出这个顶层文件夹的大小，使用后序遍历就可以实现。

又例如，当二叉树使用二叉链表存储，我们在执行销毁操作时，必须先销毁一个结点的左右子树，再销毁这个结点本身，就可以使用后序遍历实现。

 

后序遍历二叉树的算法：

 递归伪代码（摘自维基百科）

postorder(node)
  if (node = null)
    return
  postorder(node.left)
  postorder(node.right)
  visit(node)

非递归伪代码（摘自维基百科）

postorder(node)
  s ← empty stack
  lastNodeVisited ← null
  while (not s.isEmpty() or node ≠ null)
    if (node ≠ null)
      s.push(node)
      node ← node.left
    else
      peekNode ← s.peek()
      // if right child exists and traversing node from left child, then move right
      if (peekNode.right ≠ null and lastNodeVisited ≠ peekNode.right)
        node ← peekNode.right
      else
        visit(peekNode)
        lastNodeVisited ← s.pop()

 

private void _postorderTraverseRecursive(Node<Character> root , Visitor<Character> visitor)
    {
        if(root == null) return ;
        
        _postorderTraverseRecursive(root.getLeft(), visitor);
        _postorderTraverseRecursive(root.getRight(),visitor);
        visitor.visit(root.getElement());
    }
    
    public void postorderTraverseRecursive(Visitor<Character> visitor)
    {
        _postorderTraverseRecursive(root,visitor);
    }
    
    
    
    /**
     * 后序遍历非递归实现
     * */
    public void postorderTraverseLoop(Visitor<Character> visitor)
    {
        Deque<Node<Character>> stack = new LinkedList<Node<Character>>();  //使用双端队列代表栈
        Node<Character> lastNodeVisited = null , peekNode  =null;
        Node<Character> node = root;
        
        while(!stack.isEmpty() || node !=null)
        {
            if(node!=null)
            {
                stack.push(node);
                node = node.getLeft();
            }
            else 
            {
                peekNode = stack.peek();
                if(peekNode.getRight() != null && lastNodeVisited!= peekNode.getRight())
                    node = peekNode.getRight();
                else
                {
                    visitor.visit(peekNode.getElement());
                    lastNodeVisited = stack.pop();
                }
            }
        }
        
    }

 

层遍历

层遍历：对应图的广度优先遍历。层遍历也适用于一般树（generic tree）。

伪代码（摘自维基百科）

levelorder(root)
  q ← empty queue
  q.enqueue(root)
  while (not q.isEmpty())
    node ← q.dequeue()
    visit(node)
    if (node.left ≠ null)
      q.enqueue(node.left)
    if (node.right ≠ null)
      q.enqueue(node.right)

 

public void levelorderTraverseLoop(Visitor<Character> visitor)
{
    
    Deque<Node<Character>> queue =  new LinkedList<>();
    Node<Character> node = null;
    queue.addLast(root);   //入队
    while(! queue.isEmpty()) 
    {
        node = queue.removeFirst();   //出队
        visitor.visit(node.getElement());
        
        if(node.getLeft()!=null)
            queue.addLast(node.getLeft());
        if(node.getRight()!=null)
            queue.addLast(node.getRight());
    }

}

 

 

给一个二叉树的图，如何快速准确的写出 先、中、后遍历序列？

以下方法均由博主亲自实践总结。希望能帮助大家。

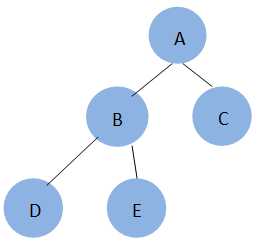
方法1：按照调用栈的流程写出函数递归调用过程，然后即可得出遍历序列。以下用先序遍历举例。其它的同理。

 

 

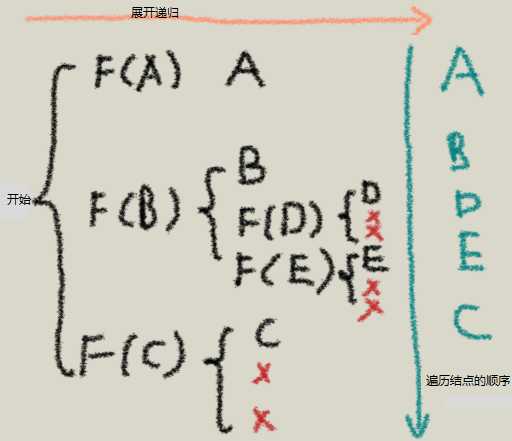
 方法2：使用画图的小技巧轻松解决。

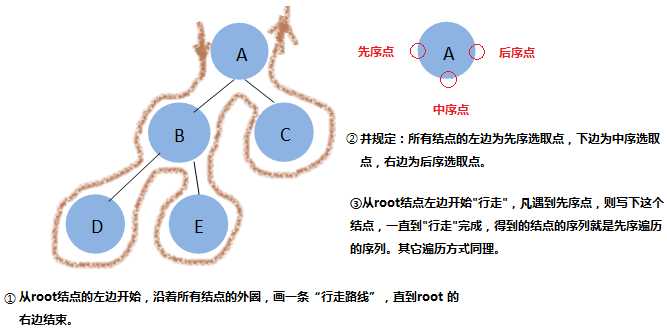
 动画演示：以中序遍历为例

 

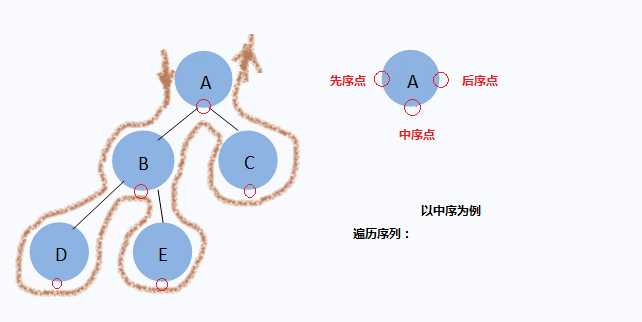
提示：这个方法中，如果使用的是RL 顺序，则需要做如下修改：
1、需要从行走路径末尾往前走，也就是从root结点的右边开始”行走“
2、将先序点和后序点交换位置：先序点位于结点的右边，后序点位于结点的左边。

如何由【中序+先序】或者【中序+后序】遍历画出树的形态？

提示：这种题，一定要给出中序遍历，否则是不能确定的。

前面我已经提到了不同遍历方法的规律：

1、先序遍历的访问的第一个结点一定是整个树的root结点。

2、后序遍历最后一个被访问的结点一定是整个树的root结点。

3、对于LR中序遍历，第一个被访问的结点一定是树的最左边的那个结点。

     对于RL中序遍历，第一个被访问的结点一定是树的最右边的那个结点。

 

 

技巧提示：重复以下步骤

1、先由先序（或者后序）确定root结点。（先后确定根结点）

2、根据root结点和中序划分左右子树。    （root中序分两边）

 

题目：

前序遍历:         GDAFEMHZ

中序遍历:         ADEFGHMZ

写出后序遍历。

 

解：

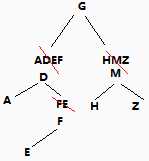
首先，由 【前序遍历:  GDAFEMHZ】确定root为G，再由root和【中序遍历:   ADEFGHMZ】，确定 ADEF是G的左子树结点，HMZ是G的右子树结点。

然后，只看左子树【ADEF】，同样先由【前序遍历: DAFE 】 确定root结点为D ， 再由 root 和【中序遍历: ADEF】 确定A是D的左子树，FE是A的右子树。

........如此重复，即可画出树的图形。