互测六 题解 9.18 圆润的多边形&Takuji与信徒

Posted 2020-10-07 Running-Coder

圆润的多边形：

我们可将所求图形划分如下：

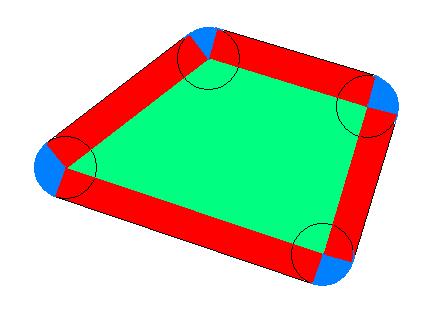
绿色部分是一凸多边形，红色部分为若干个长方形，蓝色部分为若干个扇形。

易证：1.蓝色部分的总和是一个半径为r的整圆；2.红色部分的总和=凸多边形周长*r。

那么现在就只剩下如何计算的问题。

1.对于前12.5%数据，r=0且点坐标成顺时针排列，那么直接作为凸多边形来计算即可；

2.对于前50%数据，点坐标成顺时针排列，这个部分分的做法。。。我也没想出来。。。

这是为什么呢。。。因为这个题，是我受了洛谷P1513的启发而脑补出来的，这道题中有“点坐标成顺时针排列”的限制，所以我一激动就搞出了这么个自己都不知咋做的部分分。。。见谅见谅。。。

3.对于100%的数据：

终于进入正题了。

我们先将目标放在内部的凸多边形上。

点坐标无序，如何找到一种能算的形式呢？解决方案是排序。

具体排序方法：按y坐标为第一关键字，x坐标为第二关键字，从小到大排序。

排完之后的计算方法：

1.在排序后的序列中找到第一个点和第n个点，计算一下过此两点的直线方程；

2.扫描第2~n-1个点，判断当前点与先前直线的位置关系，若在直线左侧则压入一个数组，记为l[]，在右侧则压入另一数组，记为r[]；

3.对{第一个点，第n个点，l[]}，{第一个点，第n个点，r[]}分别计算周长和面积，最后相加即可。细节请见代码。

然后，蓝色部分=πr^2，红色部分=周长*r，将这三个值相加即得最终结果。

标程：

  1 #include<cstdio>
  2 #include<iostream>
  3 #include<cstring>
  4 #include<cmath>
  5 #include<ctime>
  6 #include<cstdlib>
  7 
  8 #include<string>
  9 #include<stack>
 10 #include<queue>
 11 #include<vector>
 12 #include<algorithm>
 13 #include<map>
 14 #include<set>
 15 
 16 using namespace std;
 17 
 18 double pi=acos(-1);
 19 
 20 struct points{
 21     double x,y;
 22 };
 23 
 24 bool cmp(points aa,points bb){
 25     if(aa.y!=bb.y)return aa.y<bb.y;
 26     else return aa.x<bb.x;
 27 }
 28 
 29 double getd(points aa,points bb){
 30     return sqrt(pow((aa.x-bb.x),2)+pow((aa.y-bb.y),2));
 31 }
 32 
 33 double getv(points aa,points bb,points cc){
 34     double d1=getd(aa,bb);
 35     double d2=getd(bb,cc);
 36     double d3=getd(cc,aa);
 37     
 38     double p=(d1+d2+d3)/2;
 39     
 40     return sqrt(p*(p-d1)*(p-d2)*(p-d3));
 41 }
 42 
 43 points a[110];
 44 int n,i;
 45 
 46 points l[110];
 47 int pl=0;
 48 points r[110];
 49 int pr=0;
 50 
 51 double rr;
 52 double x11,y11,x22,y22;
 53 double k,b;
 54 double x_temp;
 55 
 56 double C,S;
 57 
 58 int main(){
 59 //    freopen("T2.in","r",stdin);
 60 //    freopen("T2.out","w",stdout);
 61     
 62     scanf("%d%lf",&n,&rr);
 63     
 64     for(i=1;i<=n;i++)scanf("%lf%lf",&a[i].x,&a[i].y);
 65     
 66     sort(a+1,a+1+n,cmp);
 67     
 68     x11=a[1].x;
 69     y11=a[1].y;
 70     x22=a[n].x;
 71     y22=a[n].y;
 72     
 73     k=(y22-y11)/(x22-x11);
 74     b=y11-k*x11;
 75     
 76     for(i=2;i<n;i++){
 77         x_temp=(a[i].y-b)/k;
 78         
 79         if(a[i].x<x_temp){
 80             pl++;
 81             l[pl].x=a[i].x;
 82             l[pl].y=a[i].y;
 83         }
 84         else{
 85             pr++;
 86             r[pr].x=a[i].x;
 87             r[pr].y=a[i].y;
 88         }
 89     }
 90     
 91     C=getd(a[1],l[1])+getd(a[1],r[1])+getd(a[n],l[pl])+getd(a[n],r[pr]);
 92     
 93     for(i=1;i<pl;i++)C+=getd(l[i],l[i+1]);
 94     for(i=1;i<pr;i++)C+=getd(r[i],r[i+1]);
 95     
 96     S=getv(a[1],a[n],l[pl])+getv(a[1],a[n],r[pr]);
 97     
 98     for(i=1;i<pl;i++)S+=getv(a[1],l[i],l[i+1]);
 99     for(i=1;i<pr;i++)S+=getv(a[1],r[i],r[i+1]);
100     
101     S+=C*rr;
102     S+=pi*rr*rr;
103     
104     C+=2*pi*rr;
105     
106     printf("%.2lf %.2lf\\n",C,S);
107     
108 //    fclose(stdin);
109 //    fclose(stdout);
110     
111     return 0;
112 }

 

 

 

Takuji与信徒：

首先你要搞一种数据结构，推荐BIT，毕竟常数小。

其次是离散化，如果不会请自行百度，就是先将坐标排序，每次操作时二分查找一下，就得到了实际操作位置。

1操作和3操作没啥可说的，只讲讲2操作。

如果开始的时候把初始序列读入并直接离散化，那么就会愉快的错掉，因为二分出的位置是不对的，2操作指定的坐标在初始序列中不存在，结果会是离散化到了其他坐标上面去。

正确的搞法如下：

1.读入原始序列，将坐标和值存入数组，记为c[]，然后不作任何操作；

2.读入指令，但不执行，而是先将指令存到数组当中，记为com[]。如果读到了2操作，那么在c[]中新存入一个元素，坐标为此次操作2指定的坐标，值为0，表示这个位置的值也有可能即将被修改，因为2操作的实质就是将一个原值为0的点进行修改；

3.对c[]进行离散化；

4.处理com[]中的指令，这时若遇到操作2，就可以采取与操作1同样的方式处理了。操作1、3不再赘述。

标程：

  1 #include<cstdio>
  2 #include<iostream>
  3 #include<cstring>
  4 #include<cmath>
  5 #include<ctime>
  6 #include<cstdlib>
  7 
  8 #include<string>
  9 #include<stack>
 10 #include<queue>
 11 #include<vector>
 12 #include<algorithm>
 13 #include<map>
 14 
 15 using namespace std;
 16 
 17 inline void read(int &x){
 18     x=0;
 19     char t=getchar();
 20     bool f=0;
 21     
 22     while(t<\'0\' || t>\'9\'){
 23         if(t==\'-\')f=1;
 24         t=getchar();
 25     }
 26     
 27     while(t>=\'0\' && t<=\'9\'){
 28         x=(x<<3)+(x<<1)+t-\'0\';
 29         t=getchar();
 30     }
 31     
 32     if(f)x=-x;
 33 }
 34 
 35 void add(int,int);
 36 int pre(int);
 37 
 38 struct abc{
 39     int rank,data; 
 40 } c[1000010],temp;
 41 
 42 int tree[1000010];
 43 
 44 bool cmp(abc x,abc y){
 45     return x.rank<y.rank;
 46 }
 47 
 48 struct bcd{
 49     int f;
 50     int d1,d2;
 51 } com[500010];
 52 
 53 int n,m,i,j;
 54 int p,l,r;
 55 
 56 int main(){
 57 //    freopen("T3.in","r",stdin);
 58 //    freopen("T3_2.out","w",stdout);
 59     
 60     memset(tree,0,sizeof(tree));
 61     
 62     read(n);
 63     
 64     for(i=1;i<=n;i++){
 65         read(c[i].rank);
 66         read(c[i].data);
 67     }
 68     
 69     read(m);
 70     
 71     for(i=1;i<=m;i++){
 72         read(com[i].f);
 73         read(com[i].d1);
 74         read(com[i].d2);
 75         
 76         if(com[i].f==2){
 77             n++;
 78             c[n].rank=com[i].d1;
 79             c[n].data=0;
 80         }
 81     }
 82     
 83     sort(c+1,c+1+n,cmp);
 84     n++;
 85     c[n].rank=2147483647;
 86     
 87     for(i=1;i<=n;i++)add(i,c[i].data);
 88     
 89     for(i=1;i<=m;i++){
 90         if(com[i].f==1 || com[i].f==2){
 91             temp.rank=com[i].d1;
 92             p=lower_bound(c+1,c+1+n,temp,cmp)-c;
 93             add(p,com[i].d2);
 94         }
 95         else{
 96             temp.rank=com[i].d1;
 97             l=lower_bound(c+1,c+1+n,temp,cmp)-c;
 98             temp.rank=com[i].d2;
 99             r=lower_bound(c+1,c+1+n,temp,cmp)-c;
100             if(c[r].rank>com[i].d2)r--;
101             printf("%d\\n",pre(r)-pre(l-1));
102             
103         }
104     }
105     
106 //    fclose(stdin);
107 //    fclose(stdout);
108     
109     return 0;
110 }
111 
112 void add(int p,int x){
113     while(p<=n){
114         tree[p]+=x;
115         p+=p&-p;
116     }
117 }
118 
119 int pre(int p){
120     int ans=0;
121     while(p>=1){
122         ans+=tree[p];
123         p-=p&-p;
124     }
125     return ans;
126 }